姓名:熊俊松________________________ 班级:2220422__________________________________ 学号:20222024234_______________________
实验题目:___________________________ **回归 **___________________________________
实验目的:
掌握回归算法的编程实现细节,要求不能使用任何库,纯手动编程实现多元线性回归。加深 对梯度计算、梯度下降算法、目标函数的求极值的理解,领会初值选取、学习率选择、公差 选择等对回归的影响。
问题描述与步骤:
1.1 搭建开发环境:
-
实验是想要用linux来实现这个程序,实验是要求用Xubuntu Linux系统来实现,但是由于我用的别的linux虚拟机来实现(VMware Workstation Pro)和下了一个终端软件来连接创建的虚拟机(FinalShell)。下面我会详细来怎么配置这个两个系统的开发环境配置:
Xubuntu Linux系统:
- 下载python解释器
sudo apt install python3-pip # Debian/Ubuntu 系统- 分别下载numpy,scipy,matploblib,sklearn,pytorch模块
pip3 install numpy pip3 install matplotlib pip3 install scipy pip3 install scikit-learnpip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cpu-
下载linux版的Vscode软件(可下可不下,只是一个编辑软件)
-
安装必要的依赖(以 Debian/Ubuntu 为例):
sudo apt install software-properties-common apt-transport-https curl -
添加 Microsoft GPG 密钥:
curl -sSL https://packages.microsoft.com/keys/microsoft.asc | sudo apt-key add - -
添加 VS Code 软件源:
sudo add-apt-repository "deb [arch=amd64] https://packages.microsoft.com/repos/vscode stable main" -
更新软件包列表并安装 VS Code:
sudo apt update sudo apt install code
VMware Workstation Pro系统
- 下载python解释器
sudo yum install python3-pip # CentOS/Fedora 系统- 分别下载numpy,scipy,matploblib,sklearn,pytorch模块(和上面一样)
pip3 install numpy pip3 install matplotlib pip3 install scipy pip3 install scikit-learnpip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cpu-
下载linux版的Vscode软件(可下可不下,只是一个编辑软件)
-
安装必要的依赖:
sudo yum install -y gcc-c++ make -
添加 Microsoft GPG 密钥:
sudo rpm --import https://packages.microsoft.com/keys/microsoft.asc -
添加 VS Code 软件源:
sudo sh -c 'echo -e "[code]\nname=Visual Studio Code\nbaseurl=https://packages.microsoft.com/yumrepos/vscode\nenabled=1\ngpgcheck=1\ngpgkey=https://packages.microsoft.com/keys/microsoft.asc" > /etc/yum.repos.d/vscode.repo' -
更新软件包列表并安装 VS Code:
sudo yum check-update sudo yum install code
-
1.2 下载数据
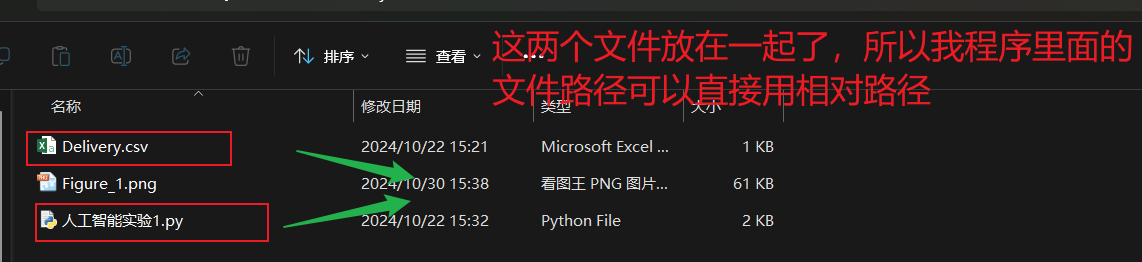
由于这个回归实验的程序需要一个表格数据(这里用csv文件),老师在客群里面发了,大家把这个文件最好放在程序的相同目录下面,当然也可以不放在相同的目录下,但是程序里面的文件路径需要修改一下。
例下:
提示:当然这个Windows系统的
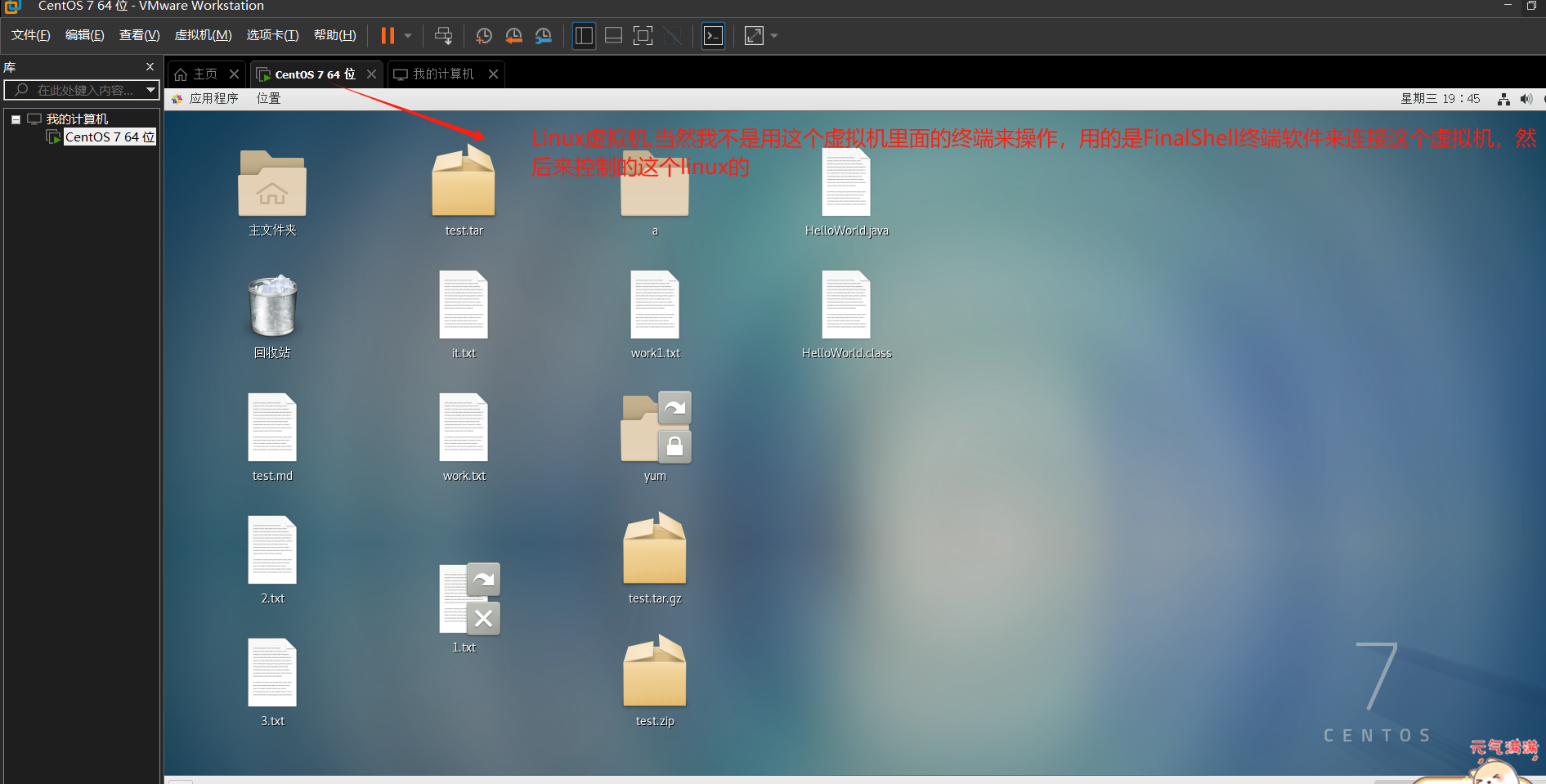
- 下面我写一下Linux系统的怎么弄呢?
- 首先打开虚拟机
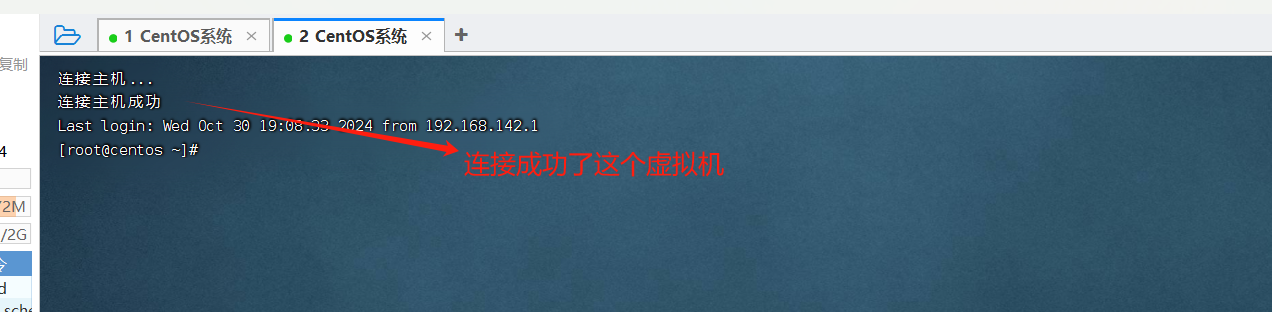
- 打开FinalShell来连接这个创建的虚拟机
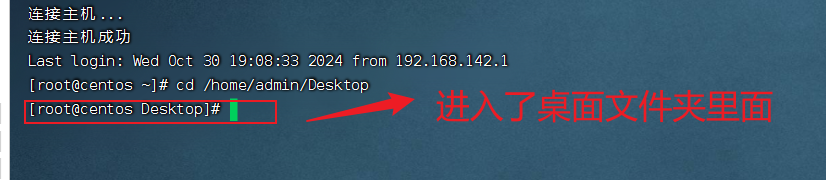
- 进入Desktop(桌面)创建一个文件夹:人工智能实验1
进入人工智能文件夹里面,并且创建:人工智能实验1.py文件
将老师的文件移到人工智能实验1这个文件夹里面
提示:移动进去了,可以看出来
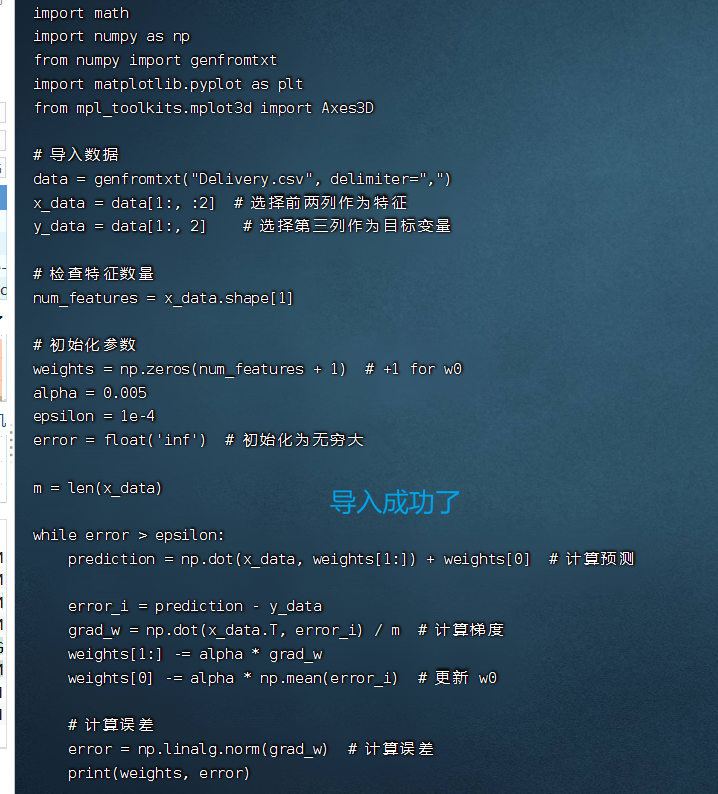
- 进入到人工智能实验1.py里面将下面的程序代码写进去
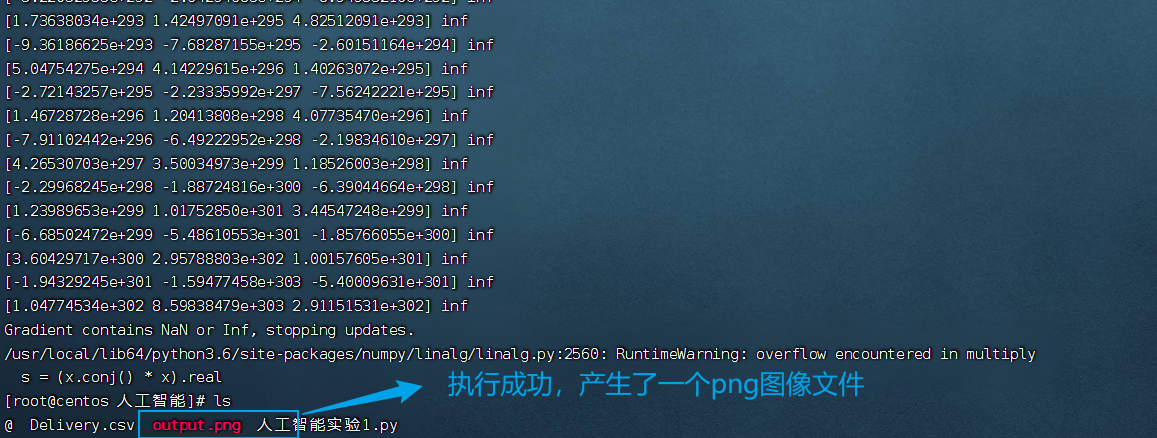
- 执行代码
- 打开这个png图像文件,由于linux没有可视化工具,我们将其移到windows里面观看
实验方法(程序):
windows(用这个):
import math
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 导入数据
data = genfromtxt("Delivery.csv", delimiter=",")
x_data = data[1:, :2] # 选择前两列作为特征
y_data = data[1:, 2] # 选择第三列作为目标变量# 检查特征数量
num_features = x_data.shape[1]# 初始化参数
weights = np.zeros(num_features + 1) # +1 for w0
alpha = 0.005
epsilon = 1e-4
error = float('inf') # 初始化为无穷大m = len(x_data)while error > epsilon:prediction = np.dot(x_data, weights[1:]) + weights[0] # 计算预测error_i = prediction - y_datagrad_w = np.dot(x_data.T, error_i) / m # 计算梯度weights[1:] -= alpha * grad_wweights[0] -= alpha * np.mean(error_i) # 更新 w0# 计算误差error = np.linalg.norm(grad_w) # 计算误差print(weights, error)# 绘制三维图
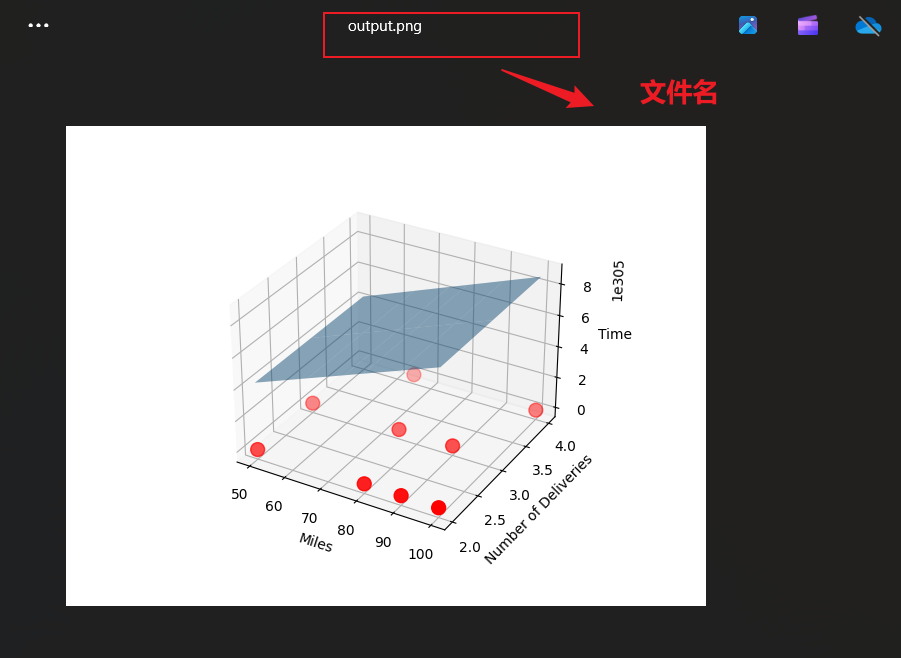
ax = plt.figure().add_subplot(111, projection='3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c='r', marker='o', s=100)x0 = np.unique(x_data[:, 0])
x1 = np.unique(x_data[:, 1])
X0, X1 = np.meshgrid(x0, x1) # 使用唯一值生成网格
Z = weights[0] + weights[1] * X0 + weights[2] * X1ax.plot_surface(X0, X1, Z, alpha=0.5)
ax.set_xlabel('Miles') # 根据需要修改标签
ax.set_ylabel('Number of Deliveries') # 根据需要修改标签
ax.set_zlabel('Time') # 根据需要修改标签
plt.show()
Linux用这个:
import numpy as np
from numpy import genfromtxt
import matplotlib
matplotlib.use('Agg') # 使用 Agg 后端
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 导入数据
data = genfromtxt("Delivery.csv", delimiter=",")
x_data = data[1:, :2] # 特征
y_data = data[1:, 2] # 目标# 初始化参数
num_features = x_data.shape[1]
weights = np.random.randn(num_features + 1) * 0.01 # 小随机值初始化
alpha = 0.001 # 学习率
epsilon = 1e-4
error = float('inf')m = len(x_data)while error > epsilon:prediction = np.dot(x_data, weights[1:]) + weights[0]error_i = prediction - y_datagrad_w = np.dot(x_data.T, error_i) / m# 检查梯度if np.any(np.isnan(grad_w)) or np.any(np.isinf(grad_w)):print("Gradient contains NaN or Inf, stopping updates.")breakweights[1:] -= alpha * grad_wweights[0] -= alpha * np.mean(error_i)error = np.linalg.norm(grad_w)print(weights, error)# 可视化并保存图像
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c='r', marker='o', s=100)x0 = np.unique(x_data[:, 0])
x1 = np.unique(x_data[:, 1])
X0, X1 = np.meshgrid(x0, x1)
Z = weights[0] + weights[1] * X0 + weights[2] * X1ax.plot_surface(X0, X1, Z, alpha=0.5)
ax.set_xlabel('Miles')
ax.set_ylabel('Number of Deliveries')
ax.set_zlabel('Time')# 保存图像
plt.savefig('output.png')实验(编程调试)过程与结果分析
Linux产生的图像:
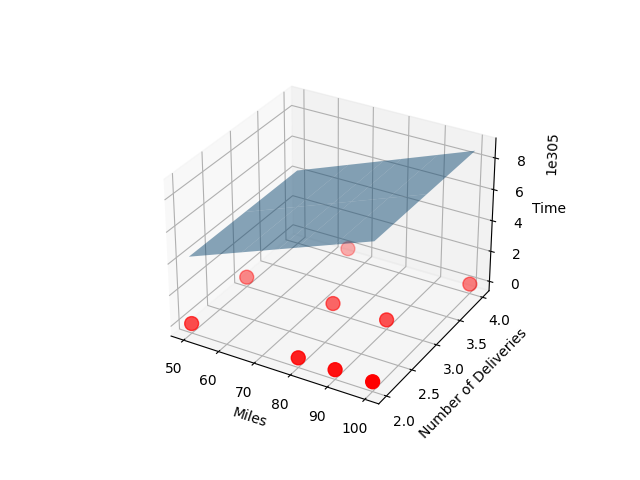
Windows产生的图像:
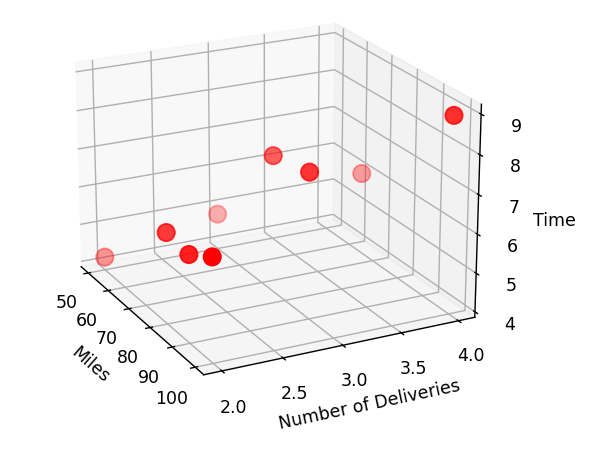
实验结论与心得:
从实验可知,这个实验是基于python编程语言去完成**多元线性回归 **的实现,所以这个实验让我们可以对python的编程语法以及思想和他的第三方模块的使用有了一定的了解,例如实验用到的numpy,matblotlib模块。
不仅如此,他还不只是可以用Windows系统的完成,还可以用Linux操作系统完成,这个实验呢对很多的人来说应该是比较难的,因为实验要求是用Linux(VMWARE系统或者XUbuntu系统)完成。
但是我觉的这个实验程序对于那些没有Linux系统基础的同学来说,Windows应该更加友好,所以我觉得大家还是用Windows操作系统的Vscode来实现这个程序实验吧,因为这个程序在那个操作系统上都可以实现(Windows或Linux),对于那些想要用Linux系统来实现的同学来说,它们应该会得到更多的知识,例如对Linux系统的认识,以及对Linux的指令的使用的了解。
但是我觉得那些不想学习深入或者学习Linux而是为了完成实验的同学来说呢,我觉得还是没必要去下那个乌班图(Xubuntu)虚拟机,不管咋样,我看了一下安装包,大概有个4~5个G,这个实验我也是收获满满,教同学完成实验,我也是更加深刻的记住了一些配置知识。