原题链接
比较简单的 \(\text{dp}\) 题。
看见题目的 \(\sum w_ih_i\) 式子,很容易想到排序不等式,所以我们先对 \(w,h\) 排序,然后分情况讨论。
-
若 \(w_i,h_i\) 对应的编号不相等,肯定是把它们配对。
-
若 \(w_i,h_i\) 对应的编号相等,考虑这样的连法:
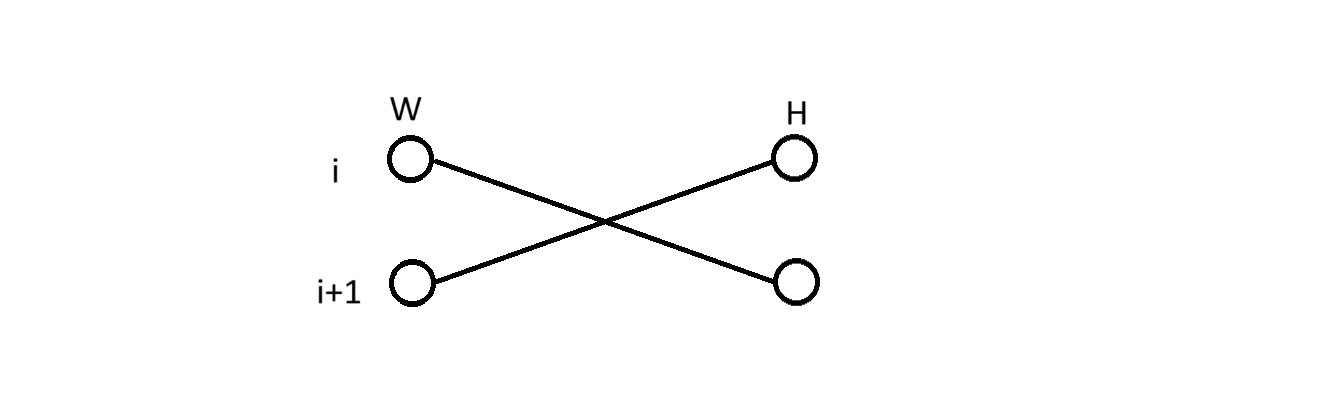
-
若是这种情况也不合法,或者它们之后又有一个点不合法,我们再加一个点,会得到两种情况:
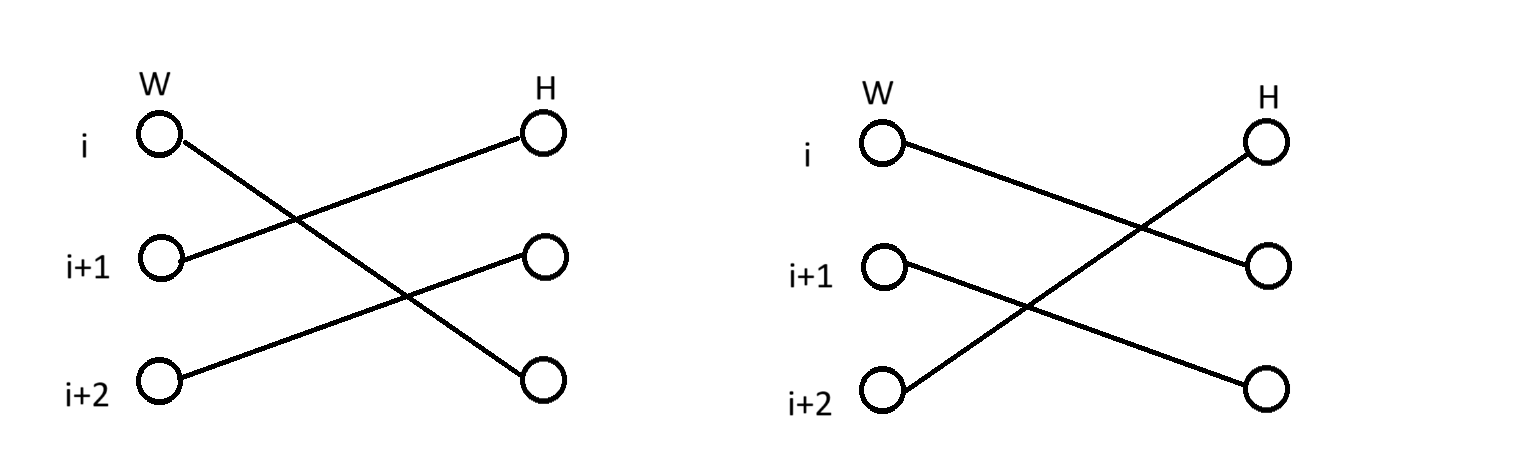
而这样一定可以得到最优,之后不合法的规模继续扩大,我们也可以拆分成上述的小问题。
所以转移方程易得:\(f_i=\max\begin{cases} f_{i-1}+w_ih_i \\f_{i-2}+w_ih_{i-1}+w_{i-1}h_i\\f_{i-3}+w_ih_{i-1}+w_{i-1}h_{i-2}+w_{i-2}h_i\\f_{i-3}+w_ih_{i-2}+w_{i-1}h_{i}+w_{i-2}h_{i-1} \end{cases}\)
从大往小进行转移,转移前注意判断是否合法,时间复杂度 \(O(nq)\),卡卡常似乎能过。
但是这个方程明显支持矩阵优化,我们列出转移矩阵,用线段树维护即可。
我们用广义矩阵乘法:\(C_{i,j}=\max_{k=1}^{m}A_{i,k}+B_{k,j}\),然后列出式子:
\(\begin{bmatrix} f_{i-1} \\f_{i-2}\\f_{i-3} \end{bmatrix}\times \begin{bmatrix}w_ih_i& w_{i}h_{i-1}+w_{i-1}h_i&\max\{式子太长懒得写\} \\0& -\text{INF} &-\text{INF} \\-\text{INF}& 0 &-\text{INF} \end{bmatrix}=\begin{bmatrix} f_{i}\\f_{i-1}\\f_{i-2} \end{bmatrix}\)
注意线段树 \(\text{pushup}\) 时的顺序,我们的转移是从大往小做的。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define rd read()
#define ll long long
#define in inline
#define FOR(i,j,k) for(int i=j;i<=k;i++)
#define ROF(i,j,k) for(int i=j;i>=k;i--)
int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;
}
const int N=1e5+10;
const ll INF=1e17;
int n,q,w[N],h[N],idw[N],idh[N],dw[N],dh[N],tmp[N];
bool cmp(int a,int b){return tmp[a]<tmp[b];}
struct matrix{ll a[3][3];matrix(){memset(a,0,sizeof(a));}matrix operator*(matrix const&T){matrix res;FOR(i,0,2) FOR(j,0,2) res.a[i][j]=-INF;FOR(i,0,2){FOR(k,0,2){ll r=a[i][k];FOR(j,0,2) res.a[i][j]=max(res.a[i][j],r+T.a[k][j]);}}return res;}
}g[N],tr[N<<2];
void pushup(int u){tr[u]=tr[u<<1|1]*tr[u<<1];}
void build(int u,int l,int r){if(l==r){tr[u]=g[l];return;}int mid=(l+r)>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);
}
void modify(int u,int l,int r,int x){if(l==r){tr[u]=g[l];return;}int mid=(l+r)>>1;if(x<=mid) modify(u<<1,l,mid,x);else modify(u<<1|1,mid+1,r,x);pushup(u);
}
void init(int x){if(idw[x]!=idh[x]) g[x].a[0][0]=1ll*w[x]*h[x];else g[x].a[0][0]=-INF;if(x>1) g[x].a[0][1]=(idw[x]!=idh[x-1]&&idw[x-1]!=idh[x])?1ll*w[x]*h[x-1]+1ll*w[x-1]*h[x]:-INF;else g[x].a[0][1]=-INF;if(x>2){bool flag=false;ll res=-INF;if(idw[x]!=idh[x-1]&&idw[x-1]!=idh[x-2]&&idw[x-2]!=idh[x])flag=true,res=max(res,1ll*w[x]*h[x-1]+1ll*w[x-1]*h[x-2]+1ll*w[x-2]*h[x]);if(idw[x]!=idh[x-2]&&idw[x-1]!=idh[x]&&idw[x-2]!=idh[x-1])flag=true,res=max(res,1ll*w[x]*h[x-2]+1ll*w[x-1]*h[x]+1ll*w[x-2]*h[x-1]);g[x].a[0][2]=res;}else g[x].a[0][2]=-INF;g[x].a[1][0]=g[x].a[2][1]=0,g[x].a[1][1]=g[x].a[1][2]=g[x].a[2][0]=g[x].a[2][2]=-INF;
}
int main(){n=rd,q=rd;FOR(i,1,n) w[i]=rd,idw[i]=i,tmp[i]=w[i];sort(idw+1,idw+1+n,cmp);FOR(i,1,n) w[i]=tmp[idw[i]];FOR(i,1,n) h[i]=rd,idh[i]=i,tmp[i]=h[i];sort(idh+1,idh+1+n,cmp);FOR(i,1,n) h[i]=tmp[idh[i]];FOR(i,1,n) dw[idw[i]]=i,dh[idh[i]]=i;FOR(i,1,n) init(i);build(1,1,n);while(q--){int x=rd,y=rd;swap(dh[x],dh[y]),swap(idh[dh[x]],idh[dh[y]]);FOR(i,dh[x],min(n,dh[x]+2)) init(i),modify(1,1,n,i);FOR(i,dh[y],min(n,dh[y]+2)) init(i),modify(1,1,n,i);printf("%lld\n",tr[1].a[0][0]);}return 0;
}