非对称加密：猫咪的双钥匙保护 (＾• ω •＾)-编程知识

非对称加密：猫咪的双钥匙保护 (＾• ω •＾)

在之前的博客中，我们讨论了对称加密算法。这种算法使用单一密钥对数据进行加密和解密，但这也带来了一些问题，例如密钥分发和共享的安全风险。为了解决这些问题，非对称加密（Asymmetric Encryption）应运而生。

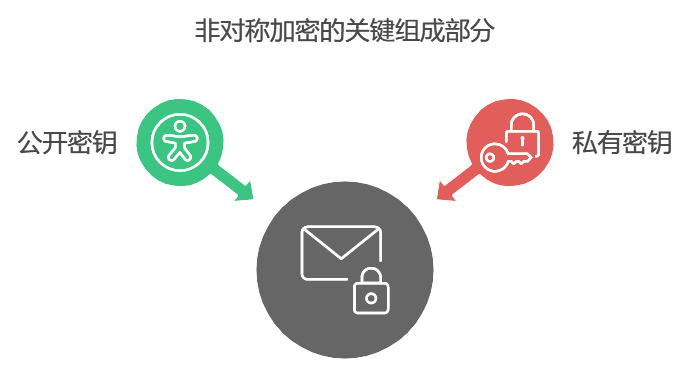
非对称加密采用了一对密钥：公开密钥（Public Key）和私有密钥（Private Key）。它们就像是猫咪小花的两把不同钥匙——一把公开给其他猫咪，另一把自己私藏，不告诉任何猫咪。只要遵循这对密钥的加密规则，猫咪们就可以放心地共享“鱼干秘密”啦！

非对称加密的基础在于一对密钥的使用：公开密钥和私有密钥。公开密钥是“公开”的，可以分享给任何人；而私有密钥是保密的，只有持有者自己知道。

猫咪小花在城堡中藏了很多小鱼干，她想让其他猫咪也能给她传递秘密信息，但又不想分享她的密钥。于是，她拿出了一把新钥匙，把它公开给大家，并告诉其他猫咪，“你们可以用这把公开的钥匙来加密信息，但解密的钥匙只有我有！” 这样，只有小花能解密信息，安全地收取其他猫咪传递来的“秘密鱼干”。

在非对称加密算法中，RSA和ECC（椭圆曲线加密）是最常见的两种算法。接下来我们简单介绍这两种算法及其特点。

RSA算法是最早也是最常用的非对称加密算法之一。它基于大数分解的数学难题，即使超级计算机也难以在短时间内解出这个问题。

RSA被广泛应用于电子邮件加密、数字签名和数据加密。它确保了安全性，但由于密钥生成和解密过程计算量较大，效率相对较低。

ECC（Elliptic Curve Cryptography）是非对称加密的一种新兴算法。它基于椭圆曲线的数学原理，能提供高效的加密效果，同时所需的密钥长度更短。

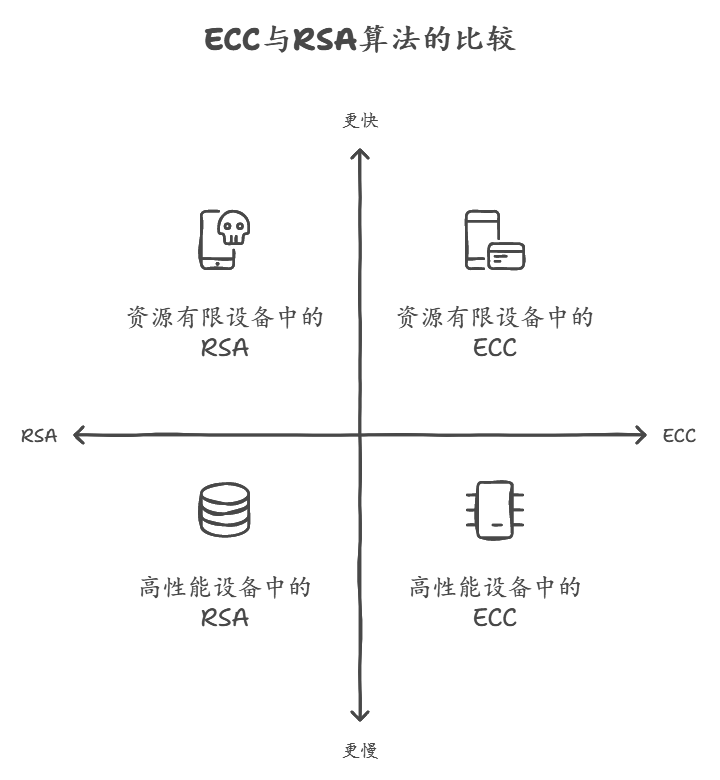
例如，猫咪小花如果想要快速、方便地保护她的鱼干信息，她可能会使用ECC。这样她既能保证鱼干安全，也不会因为加密过程太长而让自己挨饿。

非对称加密的出现大大提升了加密通信的安全性，但它也有一些不足。接下来让我们来看看非对称加密的优缺点。

由于非对称加密的高安全性和灵活性，它被广泛应用于现代互联网和信息安全领域。以下是一些常见的应用场景：

电子邮件加密：通过非对称加密，猫咪们可以安全地发送邮件，确保只有指定的收件猫咪能够解密查看。
数字证书和HTTPS：我们平时上网时，通过HTTPS协议加密数据传输，而非对称加密则确保了网页和服务器之间的安全连接，就像是猫咪们在加密信封中传递鱼干秘方。
区块链和加密货币：区块链技术和加密货币中使用了大量的非对称加密，确保交易的隐私性和不可篡改性。
数字签名：通过非对称加密，猫咪小花可以在文件上签名，保证文件的真实性和完整性，任何更改都会破坏签名。