墨卡托投影
墨卡托投影(Mercator Projection),是正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假设地球被围在一中空的圆柱里,其基准纬线与圆柱相切(赤道)接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定基准纬线上的“墨卡托投影”绘制出的地图。
投影后经线是一组竖直的等距离平行直线,纬线是垂直于经线的一组平行直线(图2-7)。各相邻纬线间隔由赤道向两极增大。一点上任何方向的长度比均相等,即没有角度变形,而长度、面积变形显著,随远离基准纬线而增大。
在地图上保持方向和角度的正确是墨卡托投影的优点,因而墨卡托投影地图常用作航海图和航空图。如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。中华人民共和国国家标准“海底地形图编绘规范”(GB/T 17834-1999)中5.1.3.1款规定 1:25万及更小比例尺图采用墨卡托投影,基本比例尺图(即1:5万,1:25万,1:100万)采用统一基准纬线30°,非基本比例尺图以制图区域中纬为基准纬线。基准纬线取至整度或整分。
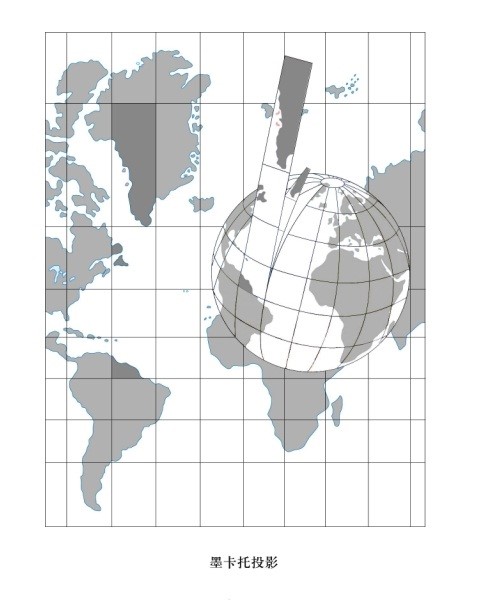
2-7 墨卡托投影示意图
高斯-克吕格投影
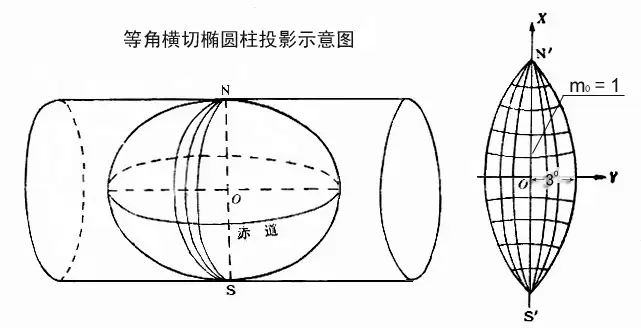
高斯-克吕格投影(Gauss-Kruger Projection)是一种等角横切椭圆柱投影,是目前大比例尺地图中应用最广的投影之一。该投影由德国数学家、物理学家、天文学家高斯于19世纪20年代拟定,后经德国大地测量学家克吕格于1912年对投影公式加以补充,故称为高斯-克吕格投影。在英、美国家也称为横轴墨卡托投影。
高斯-克吕格投影的中央经线和赤道为互相垂直的直线,其它经线均为凹向并对称于中央经线的曲线,其它纬线均为以赤道为对称轴的向两极弯曲的曲线,经纬线成直角相交(图2-8)。在这个投影上,角度没有变形。中央经线长度比等于1,没有长度变形。其余经线长度比均大于1,长度变形为正。距中央经线愈远变形愈大,最大变形在边缘经线与赤道的交点上。面积变形也是距中央经线愈远,变形愈大。
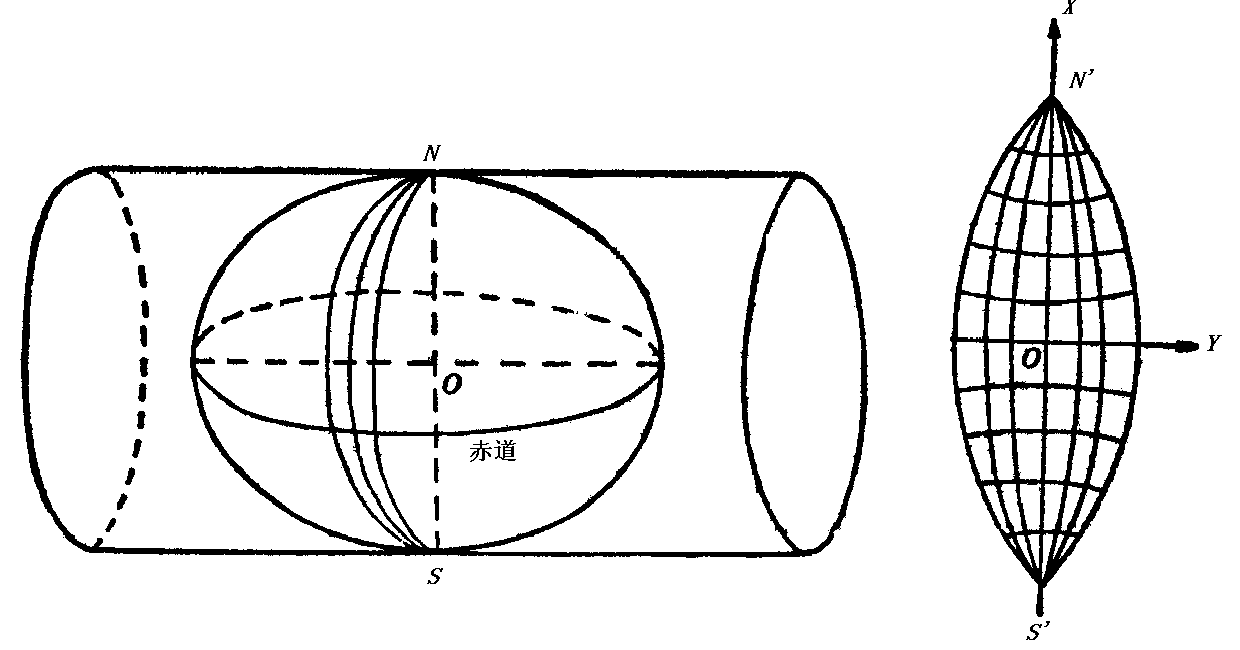
图2-8 高斯克吕格投影
为了保证地图的精度,采用分带投影方法,即将投影范围的东西界加以限制,使其变形不超过一定的限度,这样把许多带结合起来,可成为整个区域的投影。
高斯-克吕格投影有两种分带方法:6度带从0度子午线起,自西向东每隔经差6为一投影带,全球分为60带。3度带从1度30分的经线起,自西向东每隔3度为一带,全球分为120带(图2-9)。我国规定1:1万、1:2.5万、1:5万、1:10万、1:25万、1:50万比例尺地形图,均采用高斯克吕格投影。1:2.5至1:50万比例尺地形图采用经差6度分带,1:1万比例尺地形图采用经差3度分带。
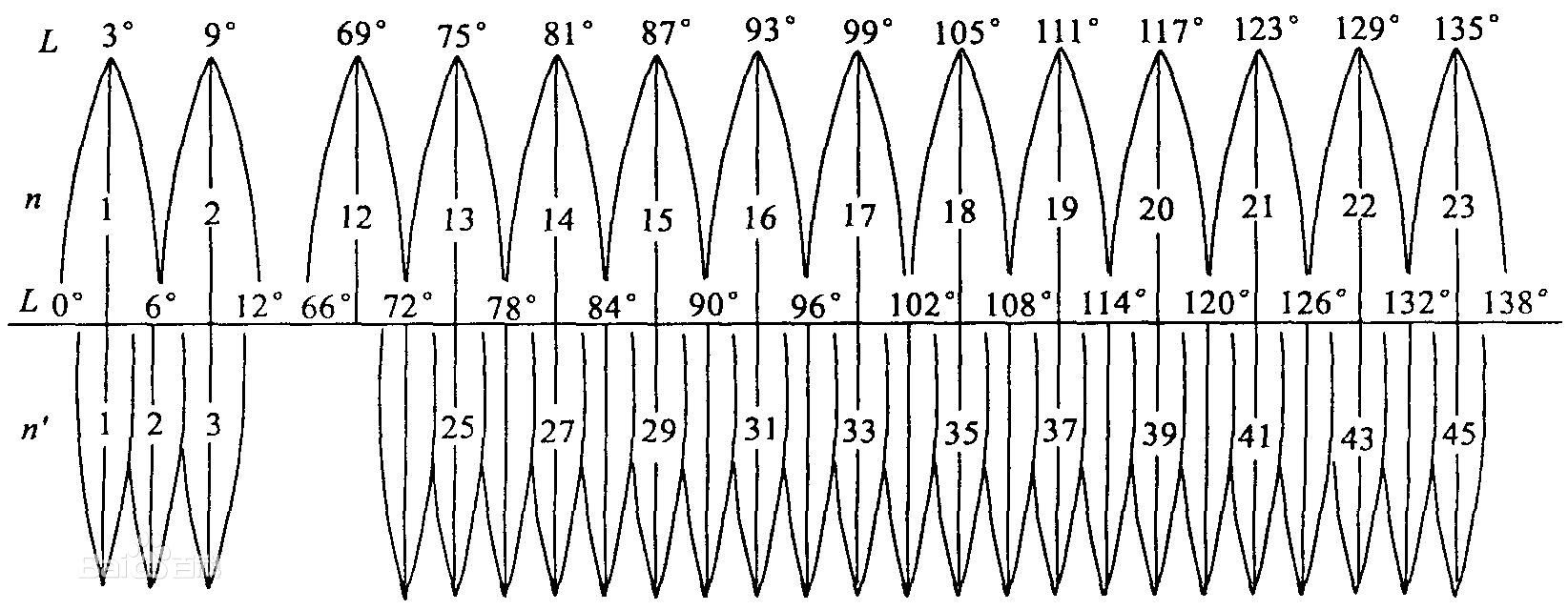
图2-9 高斯克吕格投影分带
UTM投影
UTM投影(Universal Transverse Mercator Projection,通用横轴墨卡托投影)是横轴等角割圆柱投影。此投影系统是美国编制世界各地军用地图和地球资源卫星像片所采用的投影系统,于1948年完成这种通用投影系统的计算。
椭圆柱割地球于南纬80度、北纬84度两条等高圈,投影后两条相割的经线上没有变形。如图2-10所示,左边为高斯-克吕格投影,右边为UTM投影。与高斯-克吕格投影相似,该投影角度没有变形,中央经线为直线,且为投影的对称轴,中央经线的长度比例因子取0.9996是为了保证离中央经线左右约180km处有两条不失真的标准经线。
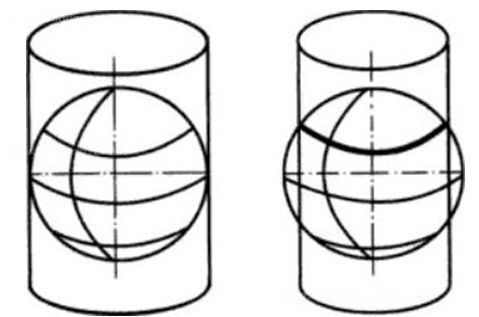
UTM投影分带方法与高斯-克吕格投影相似,将北纬84度至南纬80度之间按经度分为60个带,每带6度。将地球划分为60个投影带。我国的卫星影像资料常采用UTM投影。
高斯-克吕格投影有以下特性:
①中央子午线是直线,其长度不变形,离开中央子午线的其他子午线是弧形,凹向中央子午线。离开中央子午线越远,变形越大。
②投影后赤道是一条直线,赤道与中央子午线保持正交。
③离开赤道的纬线是弧线,凸向赤道。
通常其按经差6°或3°分为六度带或三度带。六度带自本初子午线起每隔经差6°自西向东分带,带号依次编为第1、2…60带。三度带是在六度带的基础上分成的,它的中央子午线与六度带的中央子午线和分带子午线重合,即自 1.5度子午线起每隔经差3度自西向东分带,带号依次编为第1、2…120带。我国的经度范围西起 73°东至135°,可分成六度带十一个,各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°,或三度带二十二个。

通用墨卡托投影(universal transverse Mercator projection,UTM):UTM是一种“等角横轴割圆柱投影”,椭圆柱割地球于南纬80°、北纬84°两条等高圈,投影后两条相割的经线上没有变形,而中央经线上长度比0.9996。UTM投影是为了全球战争需要创建的,美国于1948年完成这种通用投影系统的计算。
与高斯-克吕格投影相似,该投影角度没有变形,中央经线为直线,且为投影的对称轴,中央经线的比例因子取0.9996是为了保证离中央经线左右约330km处有两条不失真的标准经线。
UTM投影分带方法与高斯-克吕格投影相似,是自西经180°起每隔经差6度自西向东分带,将地球划分为60个投影带。
【两者的异同】
高斯-克吕格投影与UTM投影都是横轴墨卡托投影的变种,目前一些国外的软件或国外进口仪器的配套软件往往不支持高斯-克吕格投影,但支持 UTM投影,因此常有把UTM投影当作高斯-克吕格投影的现象。
从投影几何方式看,高斯-克吕格投影是“等角横切椭圆柱投影”,投影后中央经线保持长度不变,即比例系数为1;UTM投影是“等角横轴割圆柱投影”,圆柱割地球于南纬80度、北纬84度两条等高圈,投影后两条割线上没有变形,中央经线上长度比 0.9996。
从计算结果看,两者主要差别在比例因子上,高斯-克吕格投影中央经线上的比例系数为1,UTM投影为0.9996,高斯-克吕格投影与UTM投影可近似采用 X[UTM]=0.9996 * X[高斯],Y[UTM]=0.9996 * Y[高斯],进行坐标转换(注意:如坐标纵轴西移了500000米,转换时必须将Y值减去500000乘上比例因子后再加500000)。从分带方式看,两者的分带起点不同,高斯-克吕格投影自0度子午线起每隔经差6度自西向东分带,第1带的中央经度为3°;UTM投影自西经180°起每隔经差6度自西向东分带,第1带的中央经度为-177°,因此高斯-克吕格投影的第1带是UTM的第31带。此外,两投影的东伪偏移(False_Easting)都是500公里,高斯-克吕格投影北伪偏移(False_Northing)为零,UTM北半球投影北伪偏移(False_Northing)为零,南半球则为10000公里。
将地理坐标系进行投影后,即得到投影坐标系。最常用的适用于我国的地图有以下几种:
- 高斯克吕格(Gauss Kruger)投影
是以椭圆柱为投影面,使地球椭球体的某一经线与椭圆柱相切,然后按等角条件,将中央经线两侧各一定范围内的经纬线投影到椭圆柱面上,再将其展成平面而得。
2、通用横轴墨卡托(Universal Transverse Mercator, UTM)投影
其实质是等角横割圆柱投影,它是以圆柱为投影面,使圆柱割于地球椭球体的两条等高圈上,然后按等角条件,将中央经线两侧各一定范围内的经纬线投影到圆柱面上,再将其展成平面而得。

UTM投影和高斯克吕格投影的区别:
(1)中央经线长度比不同,UTM投影是0.9996,而高斯-克吕格投影是1。
(2)带的划分相同,而带号的起算不同。
(3)对于中、低纬度地区,UTM投影的变形优于高斯-克吕格投影。
(4)西方国家(美、英、德、法)多采用UTM投影作为国家基本地形图投影,东方国家(中、苏、蒙、朝)多采用高斯-克吕格投影作为国家基本地形图投影。
【我国规定】
我国规定将各带纵坐标轴西移500公里,即将所有y值加上500公里,坐标值前再加各带带号以18带为例,原坐标值为y=243353.5m,西移后为y=743353.5,加带号通用坐标为y=18743353.5 。我国各种大、中比例尺地形图采用了不同的高斯-克吕格投影带。其中大于1∶1万的地形图采用3°带;1∶2.5万至1∶50万的地形图采用6°带。
web墨卡托
墨卡托投影(或者是等角纵切椭球体投影)的特例,采用了球体进行投影。是大多数网络地图提供商所采用的投影方式
先介绍一下墨卡托投影:墨卡托投影,是正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即得本投影。墨卡托投影在切圆柱投影与割圆柱投影中,最早也是最常用的是切圆柱投影。
要是实在不是很想动脑子的话就玩一下这个动画点击打开链接,可以很直观的看懂原理
然后就是web墨卡托和墨卡托的区别,web墨卡托是将椭球换成圆球了,就这么简单。
web墨卡托的经纬度投影范围:经度[-180,180],维度[-85.05112877980659,85.05112877980659];
投影坐标范围:x[-20037508.3427892,20037508.3427892],y[-20037508.3427892,20037508.3427892];
具体规则
1、先根据2πR赤道周长算出投影坐标x[-20037508.3427892,20037508.3427892],
2、然后按照y轴范围与x轴范围一样长的规则定出投影坐标y[-20037508.3427892,20037508.3427892],
3、然后根据web墨卡托投影公式算出维度[-85.05112877980659,85.05112877980659],
4、经度[-180,180]这个就不用解释了。
这几个步骤中详细解释一下步骤3
x表示赤道方向,y表示子午线方向,表示经度,表示纬度,即有经纬度( ,)对应的墨卡托平面坐标即为(x*R,y*R)。然后我根据下面的公式算一下:通过投影y轴算经纬度中的纬度:Math.atan(Math.sinh(3.14))*180/3.14,直接js就可以计算,这里的3.14代替了π,π是πR/R(规定的y周范围/R)得到的。
三、使用web墨卡托原因
目前国内做数字城市方面的GIS项目、产品和公众应用,常涉及的投影方式主要有:面向局部区域的二维平面高斯投影(横轴墨卡托,横轴圆柱投影)、面向大范围(如全省、全国)的兰伯特投影(圆锥投影)、面向大范围的经纬度等间隔直投,而互联网上的大部分全国公众地图网站(百度、google、搜狗)则是另外一种就是——“web墨卡托”。
在市一级的小范围区域的GIS系统,比如规划局、国土局、建设局的系统,大都使用高斯投影,以便与地方地形图测绘、工程报建一直采用的坐标系相一致。高斯投影的特点也很明显,分带,适合小范围局部,不适合应用于大省、全国等大范围应用,若是强制按某带投影,则远离中央经线的区域的角度、距离、面积全部变形严重。
然后我们的选择就只有经纬度直投和web墨卡托了,为什么从中选择了web墨卡托呢?
经纬度直投:经纬度等间隔直投”的特点是相同的经纬度间隔在屏幕上的间距相等,程序员应该比较喜欢,没有复杂的坐标变换。但是只是在低纬度地区长度、角度、面积、形状变化比较小,越向高纬度,水平距离变长越大,很小的纬圈都变得和赤道一样长。同时要素自身会变形,长方形会变成上宽下窄的倒梯形。因为我家维度不算太高,所以感觉还可以觉得没啥事儿,但是东北人民受不了啊。 天地图曾经采用的是经纬度直投,但是现在改成web墨卡托了。
可以查看天地图地址http://map.tianditu.gov.cn/,默认为web墨卡托,按照下图设置设置为经纬度直投
效果很明显,房子全部都是歪的,成平行四边形了……
web墨卡托:纵向距离也是随着纬度增大而变长, 横向变大,同时纵向也变大,而且变化比例接近(因为0.0000X纬度引起可忽略),结果就是只把一个图形“原样放大”了,而形状却没有变化。
四、web墨卡托投影问题
1、web墨卡托虽然形状没变,但是高纬度地区的面积比真实同样放大了很多倍
同一张全中国范围图上,三亚和哈尔滨,选取同样真实面积的区域,在投出来的图上面积相差好多倍,但是他们各自区域中的图形都没变型。
其实这个这个不影响我们的需求,我们是要在同一种投影下既能实现大范围的小比例尺显示,又能在大比例尺下最大限度接近真实世界,当放大到城市、街道级别时,当前屏幕展示的仅仅是这个小范围,此时您看到的是形状、角度未变化的,符合真实世界的,当您到另一区域,也是如此。您根本“没机会”去同时感受“小三亚”和“大哈尔滨”。
2、地图切片同级别的比例尺不同
web墨卡托这种方式投影出的地图,然后切成分级瓦片,同级别的瓦片中,三亚和哈尔滨的比例尺不同,而同比例尺栅格瓦片,是存在于不同的级别中的。不过这一切仅仅是技术存储上的,与用户的感觉是没有关系的。
3、航线图是弯曲的
当我们在地球曲面上航行的时候都是挑着最近的航线飞行,一旦投影到web墨卡托上面便不再遵循两点之间直线最短的定理。所以这个地图给飞行员来说参考价值还是有待商榷
Google Maps、Virtual Earth等网络地理所使用的地图投影,常被称作Web Mercator(Web墨卡托投影)或Spherical Mercator(球面墨卡托投影),它与常规墨卡托投影的主要区别就是把地球模拟为球体而非椭球体。建议先对地图投影知识做一个基本的了解。
什么是墨卡托投影?
墨卡托(Mercator)投影,又名“等角正轴圆柱投影”,荷兰地图学家墨卡托(Mercator)在1569年拟定,假设地球被围在一个中空的圆柱里,其赤道与圆柱相接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅标准纬线为零度(即赤道)的“墨卡托投影”绘制出的世界地图。从球到平面,有个转换公式,这里就不再罗列。
Google们为什么选择墨卡托投影?
墨卡托投影的“等角”特性,保证了对象的形状的不变行,正方形的物体投影后不会变为长方形。“等角”也保证了方向和相互位置的正确性,因此在航海和航空中常常应用,使得人们查询地物的方向时不会出错。
墨卡托投影的“圆柱”特性,保证了南北(纬线)和东西(经线)都是平行直线,并且相互垂直。而且经线间隔是相同的,纬线间隔从标准纬线(此处是赤道,也可能是其他纬线)向两级逐渐增大。
但是,“等角”不可避免的带来的面积的巨大变形,特别是两极地区,明显的如格陵兰岛比实际面积扩大了N倍。(有兴趣的可以搜索"Mercator Puzzle"的游戏感受一下~)不过要是去两极地区探险或科考的同志们,一般有更详细的资料,不会来查看网络地图的,这个不要紧。

(正中央上部是“搬家”到北极的澳大利亚,我会乱说?)
为什么是圆形球体,而非椭球体?
这说来简单,仅仅是由于实现的方便,和计算上的简单,精度理论上差别0.33%之内,特别是比例尺越大,地物更详细的时候,差别基本可以忽略。
Web墨卡托投影坐标系:
以整个世界范围,赤道作为标准纬线,本初子午线作为中央经线,两者交点为坐标原点,向东向北为正,向西向南为负。
X轴:由于赤道半径为6378137米,则赤道周长为2*PI*r = 2*20037508.3427892,因此X轴的取值范围:[-20037508.3427892,20037508.3427892]。
Y轴:由墨卡托投影的公式可知,同时上图也有示意,当纬度φ接近两极,即90°时,y值趋向于无穷。这是那些“懒惰的工程师”就把Y轴的取值范围也限定在[-20037508.3427892,20037508.3427892]之间,搞个正方形。
懒人的好处,众所周知,事先切好静态图片,提高访问效率云云。俺只是告诉你为什么会是这样子。因此在投影坐标系(米)下的范围是:最小(-20037508.3427892, -20037508.3427892 )到最大 (20037508.3427892, 20037508.3427892)。
对应的地理坐标系:
按道理,先讲地理坐标系才是,比如球体还是椭球体是地理坐标系的事情,和墨卡托投影本关联不大。简单来说,投影坐标系(PROJCS)是平面坐标系,以米为单位;而地理坐标系(GEOGCS)是椭球面坐标系,以经纬度为单位。
经度:这边没问题,可取全球范围:[-180,180]。
纬度:上面已知,纬度不可能到达90°,懒人们为了正方形而取的-20037508.3427892,经过反计算,可得到纬度85.05112877980659。因此纬度取值范围是[-85.05112877980659,85.05112877980659]。其余的地区怎么办?没事,企鹅们不在乎。
因此,地理坐标系(经纬度)对应的范围是:最小(-180,-85.05112877980659),最大(180, 85.05112877980659)。至于其中的Datum、坐标转换等就不再多言。
注:除Google地图外,Bing地图、MapABC地图、百度地图、天地图等在线地图服务均采用了Web墨卡托投影,ESRI的Online地图也有使用此地图投影。除了在切片时候减少图片数量以外,也为了方便大家,均采用了Web 墨卡托投影方式,但在地图显示上面为了大家易懂,还是转换成了经纬度的方式显示。
投影坐标系统是定义平面的,即二维表面。与地理坐标系不同,投影坐标系有固定的长度,角度以及面积。投影坐标系统通常是基于一个地理坐标系统的,基于球体或者椭球体。
在投影坐标系统中,位置是用X,Y的坐标值来确定的,它的起点是格网的中心。每一个位置都有两个值,是相对于中心位置的。一个代表水平位置,一个代表投影位置。水平线以上或者垂线的右边都是正值。以下或者左边都是负值。 我国常见的投影坐标系统主要有北京54坐标系、西安80坐标系、WGS-84坐标系和国家2000坐标系。它们对应的地球椭球体参数见表2-1。
4.1 北京54坐标系
北京54坐标系(BJZ54)为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系。该坐标系的大地原点在原苏联的普尔科沃,采用多点定位法进行椭球定位,高程基准为 1954年青岛验潮站求出的黄海平均海水面。
其缺点在于:
(1)椭球参数有较大误差。
(2)参考椭球面与我国大地水准面存在着自西向东明显的系统性的倾斜,在东部地区大地水准面差距最大达+60m。这使得大比例尺地图反映地面的精度受到影响,同时也对观测量元素的归算提出了严格的要求。
(3)几何大地测量和物理大地测量应用的参考面不统一。
(4)定向不明确。
4.2 西安80坐标系
国家大地坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60公里,故称1980年西安坐标系,又简称西安大地原点。其参考椭球为GRS(1975)椭球体。
该坐标系为参心坐标系,椭球短轴Z轴平行于地球质心指向地极原点方向,大地起始子午面平行于格林尼治平均天文台子午面;X轴在大地起始子午面内与 Z轴垂直指向经度 0方向;Y轴与 Z、X轴成右手坐标系。采用多点定位,基准面采用青岛大港验潮站1952-1979年确定的黄海平均海水面(即1985国家高程基准)。
4.3 WGS-84坐标系
建立WGS-84世界大地坐标系的一个重要目的,是在世界上建立一个统一的地心坐标系。其参考椭球为WGS-84椭球体。
坐标原点为地球质心,其地心空间直角坐标系的Z轴指向BIH(国际时间服务机构)1984.0定义的地极(CTP)方向,即国际协议原点CIO,它由IAU和IUGG共同推荐。X轴指向BIH定义的零度子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系统。
4.4 国家2000坐标系
随着社会的进步,国民经济建设、国防建设和社会发展、科学研究等对国家大地坐标系提出了新的要求,迫切需要采用原点位于地球质量中心的坐标系统(地心坐标系)作为国家大地坐标系。采用地心坐标系,有利于采用现代空间技术对坐标系进行维护和快速更新,测定高精度大地控制点三维坐标,并提高测图工作效率。
为适应发展需要,根据《中华人民共和国测绘法》规定,我国建立全国统一的大地坐标系统,即国家2000坐标系。该坐标系是测制国家基本比例尺地图的基础,其参考椭球为CGCS2000地球椭球体。
2000国家大地坐标系的原点为包括海洋和大气的整个地球的质量中心。其Z轴由原点指向历元2000.0的地球参考极的方向,该历元的指向由国际时间局给定的历元为1984.0的初始指向推算,定向的时间演化保证相对于地壳不产生残余的全球旋转;X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点;Y轴与Z轴、X轴构成右手正交坐标系。
地理坐标系和投影坐标系是地图制图中常用的两种坐标系。地理坐标系是用经度和纬度来表示地球上任意一点的位置,而投影坐标系则是将地球上的三维空间投影到平面上去,以便在地图上展示。在地图制图过程中,常常需要将地理坐标系转换为投影坐标系,以便更好地展示地图信息。本文将对2000国家大地坐标系对应的投影坐标系进行介绍和分析。
1. 2000国家大地坐标系
2000国家大地坐标系是我国国家测绘局于2000年发布的新一代大地坐标系,取代了1980年国际椭球大地坐标系。该坐标系以WGS-84坐标系为基准,通过对我国国土进行大范围的GPS观测数据进行了调查和研究,是我国国土测绘工作的重要成果之一。
2. 投影坐标系
在地图制图中,为了更好地表达三维地理空间信息,常常需要将地球表面上的点投影到平面上,这就要用到投影坐标系。在国际上常用的投影方法有墨卡托投影、兰伯特投影、正投影等多种,每种投影方法都有其适用的范围和特点。
3. 2000国家大地坐标系的投影坐标系
2000国家大地坐标系对应的投影坐标系是高斯—克吕格投影。高斯—克吕格投影是一种圆柱投影,它将地球椭球面投影到圆柱面上,再展开成平面图,以实现地图的绘制和测绘。
4. 高斯—克吕格投影的特点
高斯—克吕格投影是一种等积投影,它保持了地图上面积的准确性,适用于世界各地的大范围测绘。它还具有等角性,能够保持地图上角度的准确性,使得地图具有更好的可视效果。另外,高斯—克吕格投影还能够减小纬度的变形,使得地图在不同纬度上的变形更加均匀。
5. 应用范围
2000国家大地坐标系对应的高斯—克吕格投影在我国国土测绘中得到了广泛的应用。它适用于各种比例尺的地图制图,包括区域地图、城市地图、乡镇地图等。高斯—克吕格投影也适用于地图投影的大规模生产,比如数字地图的生产和更新、卫星影像的变形配准等。
6. 结语
2000国家大地坐标系对应的高斯—克吕格投影是我国国土测绘领域的重要成果,它为我国地图制图和地理信息系统的发展提供了重要的支持。通过对该投影坐标系的研究和应用,我们可以更好地理解地图的制作原理,为地图制图工作提供更加准确和精细的技术支持。希望在未来的发展中,我们可以进一步完善这一坐标系,为地图制图和地理信息系统的发展贡献更多的力量。7. 2000国家大地坐标系在地图制图和地理信息系统中的重要性
2000国家大地坐标系是我国国土测绘领域的重要成果,对地图制图和地理信息系统具有重要的意义。它为地图的制作提供了准确的基准。地图是人们认识和了解地球表面形态和地理位置的重要工具,而地图的制作离不开准确的地理坐标系。2000国家大地坐标系的推广应用,保证了地图的准确性和真实性,使得制作的地图更加符合实际地理情况。
2000国家大地坐标系的应用推动了地理信息系统的发展。地理信息系统是一种利用计算机和地图投影技术,采集、存储、管理、分析和展示地理数据的系统,它的建设和发展需要准确的地理坐标系作为支撑。2000国家大地坐标系对应的投影坐标系,能够为地理信息系统提供准确的数据输入和展示,使得地理信息系统在土地利用规划、资源管理、环境保护等方面发挥着重要作用。
8. 高斯—克吕格投影在地图制图中的应用优势
高斯—克吕格投影作为2000国家大地坐标系对应的投影坐标系,具有许多优势对于地图制图而言。它保持了地图上面积的准确性。在实际的地图制作中,需要保证地图上不同地区的面积比例是准确的,特别是对于土地利用规划和资源分配来说,这是非常重要的。
高斯—克吕格投影具有等角性,即保持了地图上角度的准确性。这一特点使得地图上的各种角度信息能够更加真实地展现出来,为人们对地理空间的认知提供了更好的支持。它对纬度的变形有较好的抑制作用,使得地图在不同纬度上的变形更加均匀,保证了地图的整体视觉效果。
9. 高斯—克吕格投影在数字地图生产和卫星影像配准中的应用
随着科技的发展,数字地图的生产和卫星影像的应用也日益广泛,而高斯—克吕格投影也在这些领域发挥了重要的作用。在数字地图的生产中,高斯—克吕格投影能够提供准确的地理参照,使得数字地图的制作更加精准。在卫星影像的配准过程中,高斯—克吕格投影也能够保持地图的准确性和真实性,使得卫星影像和地图之间能够更好地对应和匹配。
10. 未来的发展方向
2000国家大地坐标系对应的高斯—克吕格投影在我国国土测绘和地图制图中发挥着重要的作用,但随着科技的发展和社会的需求,它也面临着一些挑战和发展的机遇。随着地图制图技术的不断发展,需要更加精细的地图制作和更准确的地理坐标系,这就需要不断完善高斯—克吕格投影,提高其精度和适用范围。另随着数字地图和卫星影像的广泛应用,需要进一步研究高斯—克吕格投影在这些领域的应用技术,提高其在数字地图制作和卫星影像配准中的效率和精度。
11. 结语
2000国家大地坐标系对应的高斯—克吕格投影作为我国地图制图和地理信息系统的重要支撑,已经在我国国土测绘和地理信息服务领域发挥着重要作用。通过对该投影坐标系的研究和应用,我们不但更深刻地理解了地图的制作原理,也为地图制图工作提供了更加准确和精细的技术支持。希望在未来的发展中,我们可以进一步完善这一坐标系,提高地图制图和地理信息系统的精准度和效率,为我国国土测绘和地理信息服务的发展贡献更多的力量。
WGS1984坐标(通常简称为WGS84)与大地2000坐标(CGCS2000)在多个方面存在显著的区别:
两者的提出时间:
WGS84是由美国国防部为了适应全球地图编制和空间技术发展的需要,在1984年建立的一种地心坐标系。它是全球定位系统(GPS)的参考构架,是全球性的地理坐标系统。
CGCS2000(中国地球坐标系统2000)是中国自主建立的新一代大地坐标系统,提出于2000年,主要基于中国境内大量的大地测量数据。
应用范围:
WGS84是全球性的坐标系统,主要用于GPS和其他全球导航卫星系统(GNSS),广泛用于全球定位系统和国际地图,适用于全球范围内的定位和导航。
CGCS2000则主要针对中国地区,更适合中国的地理特征,适用于中国境内的地图制作、土地管理、城市规划等领域。
精度:
虽然两者都使用经度、纬度和高度来表示坐标,但由于参考椭球体的不同,同一地点在两个系统下的坐标值会有所差异。CGCS2000在中国境内提供比WGS84更高的定位精度。
参考椭球体与参数:
WGS84和CGCS2000都使用了地心坐标系,但它们的原点都位于地球质心,但采用了不同的参考椭球体模型。WGS84采用的椭球参数包括长半轴为6378137m,扁率为1/298.2572235633。而CGCS2000的长半轴同样为6378137m,但扁率为1/298.257222101,其椭球体参数更适合中国的地理特征。
坐标转换:
由于WGS84和CGCS2000采用了不同的参考椭球体模型,因此同一地点在两个系统下的坐标值会有所不同。将基于WGS84的坐标转换为基于CGCS2000的坐标涉及到复杂的大地测量学和地理信息系统(GIS)的知识。在编程层面,这种转换通常需要使用专业的库或API,例如Proj/Proj4、GDAL/OGR或GIS软件的SDK等。
- CGC2000投影坐标系: 国家2000是中国国家大地坐标系的一种版本,于2000年开始使用。它是中国地理信息系统(GIS)和地理测量的标准坐标系。国家2000采用高斯克吕格投影(Gauss-Krüger Projection)(等角横轴切椭圆柱投影)作为投影方式,将地理坐标(经纬度)转换为平面坐标。在国家2000投影坐标系中,中国的大地基准面和投影带宽度被分割为若干个投影带,每个带都有一个中央经线,使得地图上的每个点都可以用平面坐标(通常以米为单位)表示。
- WGS84投影坐标系: WGS84是一种广泛使用的地球坐标系统,用于全球定位和导航。它基于地球的椭球体模型,并使用经纬度(纬度和经度)来表示位置。WGS84经纬度坐标通常以度为单位,并且经度以西经和东经为正负值,纬度以南纬和北纬为正负值。WGS84投影坐标系通常使用墨卡托投影(Mercator Projection)或通用横轴墨卡托投影(Universal Transverse Mercator,UTM)&