置换，群论初探

news/2024/11/6 19:37:55/文章来源:https://www.cnblogs.com/oceansofstars/p/18522459

写的不好别D啊，算是一些知识的归纳（~~虽然也是看的别人的学的吧~~）

群论

仙姑

置换

置换与排列

对于一个集合 $D$ ，其大小为 $|D|$，而排列是指这 $|D|$ 个元素按照某种规定按一定顺序进行重新组成。而置换是指对这 $|D|$ 个元素重新排列，不同元素之间交换位置，从而形成新的排列。同时，集合 $D$ 可以形成的置换数目为 $|D|!$,注意 0！=1，指空集合只有一个置换，即为空置换。

置换的表示

置换用符号 $\sigma$ 表示，例如对于排列1，2，3，4，5，6，其一个置换为 $\sigma=364152$,其中 $\sigma(1)=3,\sigma(2)=6...\sigma(6)=2$。常表示为$\sigma=\begin{pmatrix}x_1&x_2&\cdots&x_n\\x_{p_1}&x_{p_2}&\cdots&x_{p_n}\end{pmatrix}.$,这实际上就是有限集 $X$在自身上的双射,而一个集合上的置换在函数合成运算下构成一个群，称为对称群。对称群的一个n元子群是n元置换群，这里不过多叙述。

轮换分解

还有一种表示方法叫轮换分解，具体方法看oi-wiki，不写了，像上面提到的例子可以轮换表示为 $\sigma=(134)(26)(5)=(134)(26)$ ，每一对括号中，都是一个轮换。括号中的元素个数，称为对应轮换的长度。实践中，常常省略掉长度为一的轮换。恒等变换中所有的轮换长度都是一，常常记作 $(1)$ 而不是全部省略

置换的轮换分解由于其特殊的循环性质，导致其可以清晰的用几何表示，将置换中的一组数 $(x,\sigma(x))$ 看作一条边，则整个置换便是由若干个不相交的环构成的，每一个环就代表了一个轮换。任何置换都可以写成一系列对换的乘积，我们考虑一下一次对换对轮换的影响。

1：两个元素属于同一轮换：

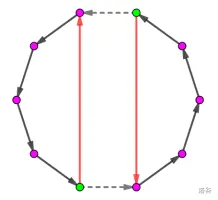
2：两个元素属于不同轮换：

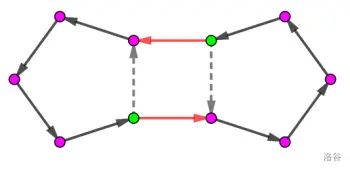
从上图可知，一次对换会使置换的轮换数变化 $1$,这也证明了一次对换必定改变置换的奇偶性。

置换的乘法

就是置换的复合，即如果有两个置换

\[f=\begin{pmatrix}x_1&x_2&\cdots&x_n\\ x_{p_1}&x_{p_2}&\cdots&x_{p_n}\end{pmatrix},\ g=\begin{pmatrix}x_{1}&x_2&\cdots&x_{n}\\ x_{q_1}&x_{q_2}&\cdots&x_{q_n}\end{pmatrix} \]

那么他们的乘积为

\[f\circ g=\begin{pmatrix}x_1&x_2&\cdots&x_n\\ x_{q_{p_1}}&x_{q_{p_2}}&\cdots&x_{q_{p_n}}\end{pmatrix}\]

置换的性质

奇偶性

置换分解成一系列对换的方式不是唯一的(毕竟只考虑结果，过程很多样)，但分解出来的对换的个数的奇偶性是相同的，可以用上面的那个结论证明。而一个置换的对换分解的数目的奇偶性就是置换的奇偶性。

一个快速判断置换奇偶性的式子，设 $n$ 个元素做轮换分解后有 $k(\sigma)$ 个轮换，则置换 $\sigma$ 的奇偶性与 $n-k(\sigma)$ 相同。

$n>=2$ 时，$n$ 元置换群中奇置换和偶置换数目相等

证明：我们设$S_n$表示 $n$ 元置换群， $X=\{s_1,s_2\cdots s_m\}$ 表示全部其中的全部奇置换，$Y$ 表示其中的全部偶置换，取群中任意对换 $\sigma$，对于$X$ 中任意置换 $s_i$ ,根据群的封闭性，都有 $\sigma \cdot s_i \in S_n$ ,又因 $\sigma \cdot s_i$ 是偶置换，则 $\sigma \cdot s_i \in Y$，又因群内置换各不相同,所以 $X,Y$ 的个数均为 $S_n$ 大小的一半，即 $\frac{n!}{2}。$

置换的阶

置换的阶（order）是指满足如下条件的最小正整数 $a$：重复该置换 $a$ 次后，所有元素都回到了原位。即$$\operatorname{ord} \sigma = \min \begin{Bmatrix} a \in \mathbf N_+: \sigma^a=(1) \end{Bmatrix}.$$
一个置换的阶也等于其轮换分解后的，每一个轮换长度的 $lcm$ 。