3 有限体积法:推导方程
基本原理和目标
(注意:这一节看不懂没关系,在后面的推导中会慢慢用到)
-
质量、动量和能量的守恒
- 流体的质量守恒
- 动量改变的速度 = 一个流体粒子上受到的力的总和(牛顿第二定律)
- 能量改变的速度 = 一个流体粒子吸收的热量,和作用在其上的功的总和(热力学第一定律)
-
推导出控制流动的偏微分方程
-
通过牛顿模型描述粘性应力,推导出纳维-斯托克斯方程
-
控制流体行为的方程和传输方程是相似的
-
把传输方程的积分形式应用于有限时间间隔和有限控制体积
-
把物理现象分为椭圆型、抛物线型、双曲线型
-
将流体看作一个连续体(continuum)
-
考虑一个小流体元素,其边长为\(\delta x\),\(\delta y\),\(\delta z\)
三维物理量守恒
质量守恒
一个流体元素中质量的增加速度 = 流入流体元素的净流动速度
质量增加速度:
注意:这里\(\rho\delta x\delta y\delta z\)可理解为\(\rho \delta V\),也就是代表了该流体微元的总质量。
然后求质量关于时间的一阶导,就是质量的净增加速度了。
穿过流体元素边界,流入流体元素的净质量流动速率为:
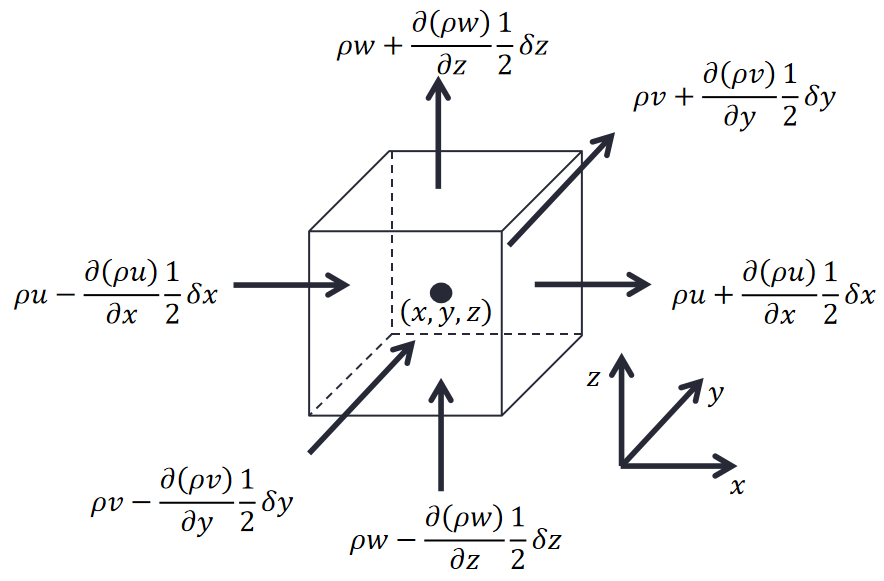
其中,约定流入流体微元的质量流动标正号,流出的标负号。
注意这里是如何运用泰勒级数展开的(以x方向,即图中横着的方向为例):
-
在点x处的质量流动速率密度(即单位面积的质量流率)为\(\rho u\);
-
使用一阶泰勒级数展开:
\[\begin{align}f(x+\delta x)=f(x)+\frac{df(x)}{dx} \delta x\end{align} \] -
在\(x-\frac{1}{2} \delta x\)(即流入处):
\[\begin{align} f(x-\frac{1}{2}\delta x)&=f(x)-\frac{\partial f(x)}{\partial x}\cdot \frac{1}{2}\delta{x}\\ &=\rho u-\frac{\partial (\rho u)}{\partial x}\cdot \frac{1}{2}\delta{x} \end{align} \]在\(x+\frac{1}{2} \delta x\)(即流出处)同理,此处不再展示。
-
x方向流入的真正质量流动速率为(即乘上个截面面积):
\[\begin{align}\left(\rho u-\frac{\partial(\rho u)}{\partial x}\frac12\delta x\right)\delta y\delta z\end{align} \]
把六个方向(x,y,z方向的流入和流出)加一下,可得:
化简可得最终穿过流体元素边界,流入流体元素的净质量流动速率:
那么,我们可以得到质量守恒方程:
把\(\delta x \delta y \delta z\)消掉,可得:
注意,这里的Nabla算子:
上述方程可表示在可压缩流体中的某一点,非稳态、三维流动下的质量守恒或连续性方程。
而对于不可压缩流动,密度是守恒的,此时:
推广:物理量守恒
现设有一物理量在每单位质量的值为\(\phi\)。
沿着一个流体粒子的轨迹,对函数\(\phi\)的总(total)或实质(substantive)导数可表示为:
注意,流体粒子会随着流动而移动,故:
由此可得,\(\phi\)的实质导数可写作:
该方程表示,该物理量随着时间的变化+流体粒子在空间中的运动与物理量在空间中变化的叠加效应=单位质量物质的\(\phi\)属性沿着一个流体微元运动轨迹的总变化率。
那么,对于一个流体粒子而言,其物理量\(\phi\)每单位体积的变化速度为:
下一步,我们向任意守恒的物理量(arbitrary conserved property)推广(generalize)出其守恒方程:
(注意:别直接用这个方程,这个是来自PPT的,请参见下面的方程27)
其具体推导过程为:
-
原实质导数参见方程17:\(\frac{D\phi}{Dt}=\frac{\partial\phi}{\partial t}+\boldsymbol{u}\cdot\nabla\phi\)
-
首先,推广到密度和物理量一起,即考虑\(\rho \phi\)随时间的变化率,此时使用乘积法则:
\[\begin{align} d(uv)=udv+vdu \end{align} \]利用该法则,有:
\[\begin{equation}\frac{\partial(\rho\phi)}{\partial t}=\phi\frac{\partial\rho}{\partial t}+\rho\frac{\partial\phi}{\partial t} \end{equation} \] -
下一步,考虑\(\rho \phi\)在空间上的变化,加入流体运动速度\(\boldsymbol{u}\)(这里加粗代表x,y,z三个方向的速度矢量),即对\(\rho \phi \boldsymbol{u}\)取散度,三个物理量都可能随着位置变化:
\[\begin{equation}\nabla\cdot(\rho\phi\vec{u})=\phi[\nabla\cdot(\rho\vec{u})]+(\rho\vec{u})\cdot\nabla\phi \end{equation} \] -
将过程2和过程3的结果,即时间导数和空间上的散度项结合起来:
\[\begin{align}\frac{\partial(\rho\phi)}{\partial t}+\nabla\cdot(\rho\phi\vec{u})=\left(\phi\frac{\partial\rho}{\partial t}+\rho\frac{\partial\phi}{\partial t}\right)+(\phi(\nabla\cdot(\rho\vec{u}))+\rho\vec{u}\cdot\nabla\phi) \end{align} \] -
根据连续性方程,质量守恒要求:
\[\begin{equation}\frac{\partial\rho}{\partial t}+\nabla\cdot(\rho\vec{u})=0 \end{equation} \]注意到方程23中:
\[\begin{equation}\phi \frac{\partial\rho}{\partial t}+\phi \cdot \nabla\cdot(\rho\vec{u})=0 \end{equation} \]故结合后的方程可写作:
\[\begin{equation}\frac{\partial(\rho\phi)}{\partial t}+\nabla\cdot(\rho\phi\vec{u})=\rho\frac{\partial\phi}{\partial t}+\rho\vec{u}\cdot\nabla\phi \end{equation} \] -
注意到方程26中右侧项恰等于\(\rho\)乘以\(\frac{D\phi}{Dt}\)。故可将推广后的守恒方程写作:
\[\begin{equation}\frac{\partial(\rho\phi)}{\partial t}+\nabla\cdot(\rho\phi\vec{u})=\rho\left(\frac{\partial\phi}{\partial t}+\vec{u}\cdot\nabla\phi\right)=\rho\frac{D\phi}{Dt} \end{equation} \]其物理意义为:
\[物理量\phi随时间的变化率+净流出速率=总变化率 \]
动量守恒