Dining G
一个点有两重限制,将点放中间,两边分别放两个限制,中间点点拆点连 1 表示限制
CTSC1999 家园 / 星际转移问题
时间限制可以分层图,分层图不需二分,直接一层层建即可
企鹅游行
这种有限制的拆点就完了。
猪
时序问题按照时间建即可。
一般出现调整的可以考虑把调整的看成流量
P1345 奶牛的电信Telecowmunication
删点可以拆点后两点之间连 1 边
花费最少->最小割(割掉一条边相当于选)
收益最大->总权值减最小割 (割掉一条边相当于不选)
【例题1】任务分配
[P2057 SHOI2007] 善意的投票 / [JLOI2010] 冠军调查
花费最少,即最小割
如何满足两点选择不同就加代价?
向两点之间连双向边即可。
P1361 小M的作物
花费最大,总代价减最小割。
两点(多点)相同有贡献。
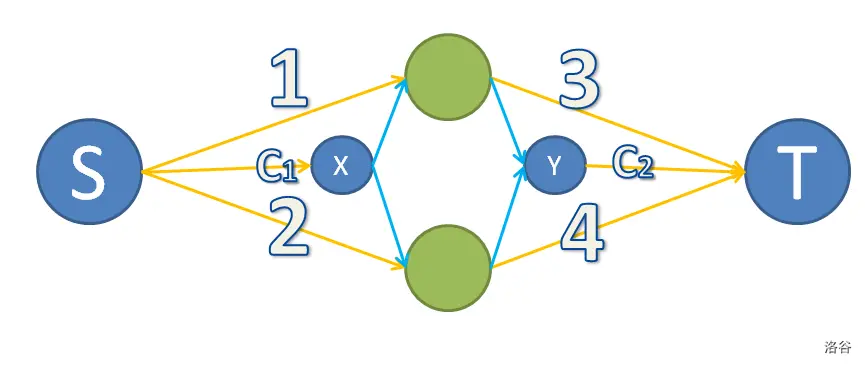
若割掉 \(1,2\) ,则 \(c_1\) 也需要割(否则割掉 \(3,4,c_2\) ,那就不需要割 \(1,2\) 了)
\(3,4\) 同理
若选择 \(1,4/2,3\) ,则 \(c_1,c_2\) 都割掉
P4126 AHOI2009 最小割
最小割集:残余网络上从S出发bfs,连接被S标记的点和未被S标记的点即为割边。
找最小割必须边:
- 从S开始BFS跑残量网络。
- 从T开始反向BFS跑残量网络。
- 枚举从S指向T的满流边,这些边即为必须边
找最小割可行边:
-
满流
-
删掉后找不到u -> v的路径
残余网络中 tarjan 跑 SCC, \((u, v)\) 的 \(u, v\) 都在同一 SCC 中说明存在残量网络 \(u \to v\)的路径
多源汇最大流:超级源点向每个源点连 \(inf\),汇点同理
无源汇上下界可行流:
先让所有边都为 \(l\) ,处理每个点入流量-出流量。
\(x > 0\) ,源点向 \(u\) 连 \(x\) ,相当于需要源点帮助流入
\(x < 0\) ,\(u\) 向汇点连 \(-x\) ,相当于需要汇点帮助流出
判断最大流是否等于源点连边。即是否满流
有源汇上下界可行流:
源点 \(t\) 向 \(s\) 流 \([0,inf]\) 平衡流量即可。
此时这条边的流量即为可行流时流量。
有源汇上下界最大流:
跑完可行流再跑一遍,相加。
有源汇上下界最小流:
跑完可行流再跑 \(t\) 到 \(s\) 最大流,相减。
最大权闭合子图:
一张有向无环图,点有点权(可能为负),对于边 \((u,v)\),如果选择 \(u\) ,就必须选择 \(v\)。求所选的点的最大权值和。
点权为正,连 \((s,u,w)\) ,相当于放弃正点
点权为负,连 \((u,t,-w)\) ,相当于选择负点
其他边连 \((u,v,inf)\)
答案为正权点和-最小割
P2805 NOI2009 植物大战僵尸
P4174 NOI2006 最大获利
费用流:
注意dfs时的vis。
若有负代价环可以先强制费用为负的边满流,跑上下界有源汇费用流即可
NOI2008 志愿者招募
NOI 2008 志愿者招募 employee (byvoid.com)
线性规划建图。