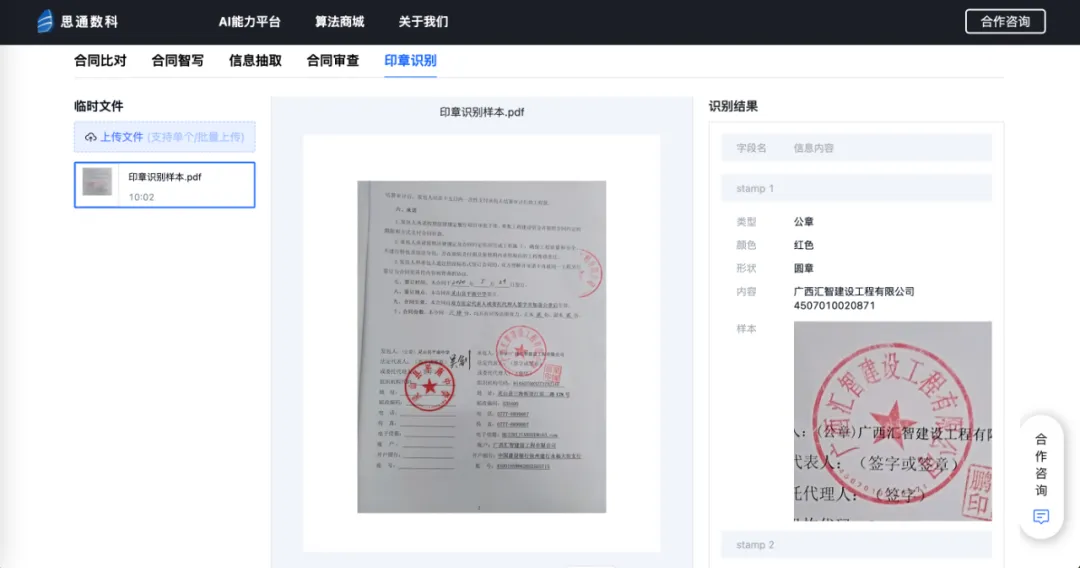
A
点仙人掌形成的沙漠,求删 \(k\) 条边使得联通块数最多是多少。
考虑先删桥,然后删环,每个环都需要断一条边没有贡献,此后没断一条边都多一个联通块。
所以考虑把环从大到小排序。
B
有 \(\{1, 2, ... , n\}\) 的所有非空子集,划分为两部分,对于在一部分的两个子集,他们的并一定也在改部分内。其中第一部分必须含有其中某 \(m\) 个子集,且第一部分的大小为 \(k\)。\(n\le 18\)。
构造答案。
注意到,势必存在一个 \(x\) 满足所有包含 \(x\) 的子集都被属于一个部分。
同时,将所有包含 \(x\) 的子集都划分给一部分后,对于剩下的所有子集,仍然存在这样的 \(x\)。
相当于进行 \(n\) 次划分,每次划分 \(2^{n-i}\) 个数给某个部分,
那么这样我们可以划分子任务,不妨设 \(f_s\) 表示能否把 \(s\) 集合的子集选 \(k\bmod 2^{|S|}\) 个出来给第一部分。
转移:如果划分给第一部分需要满足 \(k\) 存在当前这个二进制位;否则需要满足没有不合法的子集。
可以考虑用高维前缀和来处理。
C
有一排 \(n\) 个格子,每个格子有颜色,\(q\) 次询问从某点移动到另一个点所需的时间。\(n,q\le 1e6\)。
每秒钟可以进行以下两种操作之一。
将某个格子染成一种颜色;移动到相邻的格子,前提要求移动前和移动后的两个格子的颜色相同。
设 \(s<t\),从 \(s\) 移动到 \(t\)。首先 \(t-s\) 的时间用于移动。额外 \(t-s\) 的时间用于将当前格子染成上一个。
考虑颜色相同的两个位置,将其中所有颜色都染成改颜色,就可以减少 \(1\) 的贡献。
相当于选出 \([s,t]\) 区间里选最多的只在端点处相交的区间。考虑倍增处理出跳 \(2^i\) 次最近跳到哪即可。
D
一棵树强制在线,每次删一个点,问剩下的点形成的点对最短距离是多少以及个数。
考虑点分树,点分树上每个点维护该点为根的路径最长的个数以及次长的个数。