简单矩阵求导 $\frac{ \part (A \times X) }{ \part X }=A$。证明如下,自行体会。

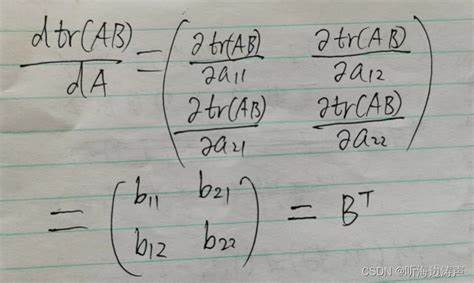
感谢 https://www.cnblogs.com/sunny99/ sumoier对本文的帮助
简单矩阵求导 $\frac{ \part (A \times X) }{ \part X }=A$。证明如下,自行体会。

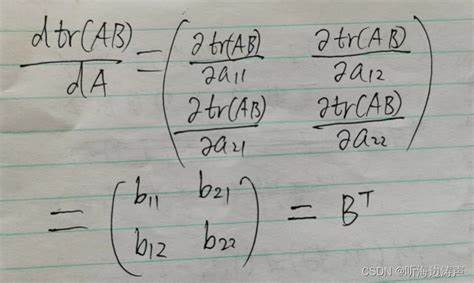
感谢 https://www.cnblogs.com/sunny99/ sumoier对本文的帮助
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/827828.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!