[T241107] 设 \(\mathscr F\) 是一个含空集的子集类, \(\mu\) 是 \(\mathscr F_0\) 上的一个满足 \(\mu(\varnothing)=0\) 的非负集函数. 对 \(A\subset \Omega\), 定义:
约定如果 \(\mathscr F_0\) 没有可列个集合可以覆盖 \(A\), 那么 \(\mu^*(A)=+\infty\), 则 \(\mu^*\) 是一个外测度.
Proof: 只需验证 \(\mu^*\) 符合外测度的定义.
(Step1.) 验证 \(\mu^*(\varnothing)=0\). 事实上, 注意到 \(\cup_n\varnothing\supset\varnothing\), 于是
从而 \(\mu^*(\varnothing)=0\).
(Step2.) 验证单调性. 设 \(A\subset B\subset\Omega\), 注意到
故单调性成立.
(Step3.) 验证次可列可加性. 设 \(\{A_n\}_{n=1}^{+\infty}\subset \mathscr F_0\).
-
若 \(\exists n_0,~s.t.~\mu^*(A_{n_0})=+\infty\), 由 \(\mu^*\) 的定义形式可知 \(\mu(A_{n_0})=+\infty\). 注意到 \(\bigcup\limits_n A_n\subset\bigcup\limits_n A_n\), 于是
\[\begin{aligned} \mu^*\left(\bigcup_nA_n\right)&=\inf\left\{\sum_n\mu(B_n):\{B_n\}\subset\mathscr F_0,~\bigcup_nB_n\supset \bigcup_nA_n\right\}\\ &\le\sum_n\mu(A_n)=+\infty. \end{aligned} \]因此
\[\mu^*\left(\bigcup_nA_n\right)\le+\infty=\mu^*(A_{n_0})\le\sum_n\mu^*(A_n). \] -
若对 \(\forall n,~\mu^*(A_n)<+\infty\). 则每个 \(A_n\) 都能被 \(\mathscr F_0\) 中可列个集合覆盖. \(\forall\varepsilon>0\), 对于每个 \(n=1,2,\cdots\), 取 \(\{A_{n,k}\}_{k=1}^{\infty}\subset\mathscr F_0\) 使 \(\bigcup\limits_kA_{n,k}\supset A_n\), 且
\[\mu^*(A_n)+\frac{\varepsilon}{2^n}>\sum_k\mu(A_{n,k}), \]又 \(\bigcup\limits_n\bigcup\limits_k A_{n,k}\supset\bigcup\limits_n A_n\), 故
\[\mu^*\left(\bigcup_nA_n\right)\le\sum_n\sum_k\mu(A_{n,k})<\sum_n\mu^*(A_n)+\varepsilon. \]由 \(\varepsilon\) 的任意性可知
\[\mu^*\left(\bigcup_nA_n\right)\le\sum_n\mu^*(A_n). \]综上, 次可列可加性也成立. #

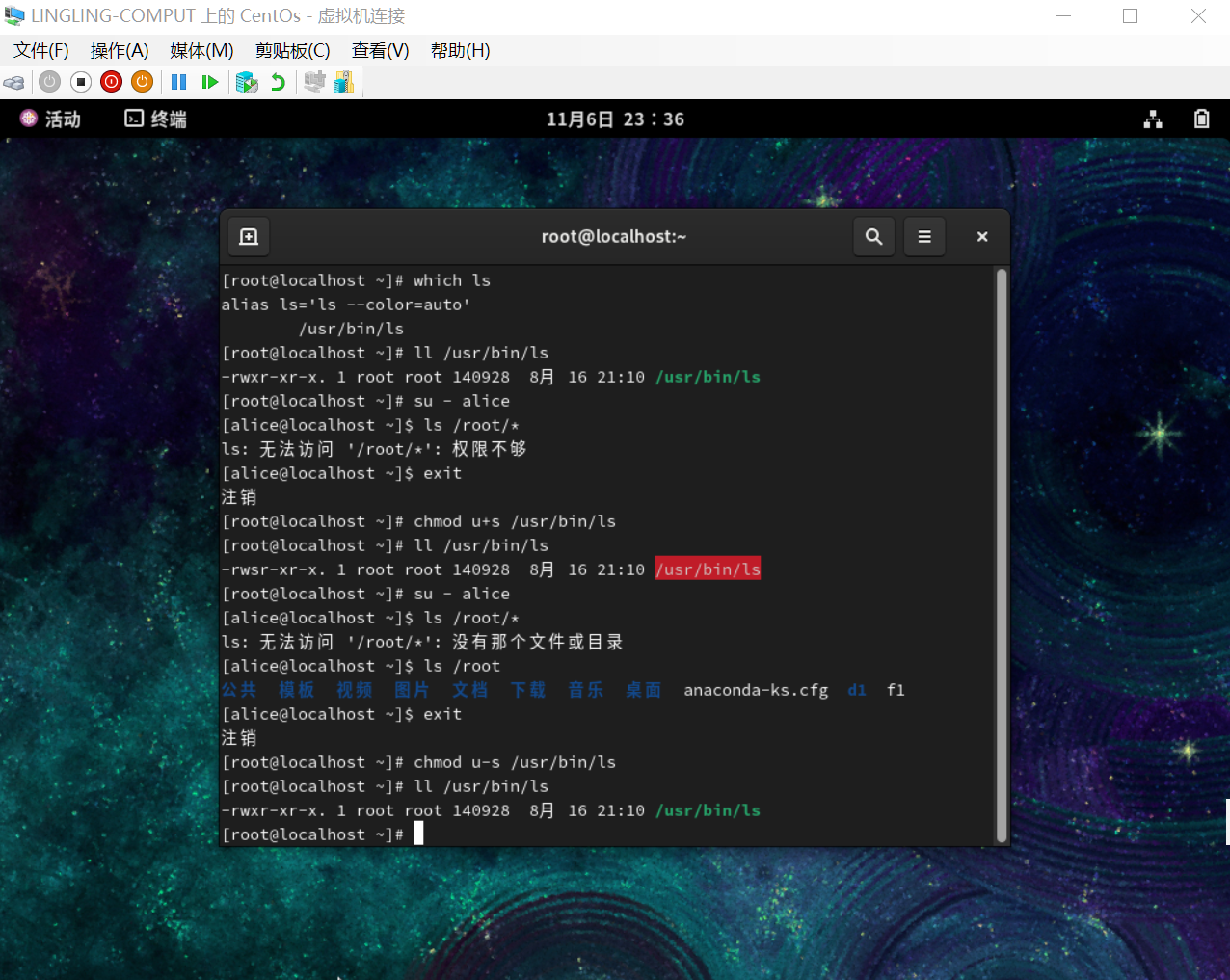
![LeetCode3264[K次乘运算后的最终数组I]](https://img2024.cnblogs.com/blog/3512406/202411/3512406-20241106162122694-346588470.png)