一、引入
学习一个新的数据结构或者算法前,我们都要了解其用途,毕竟用途才是其被发明出来的原因。那么树链剖分有什么用呢?它维护的是什么样的信息呢?这里我们只探讨重链剖分。
树链剖分用于将树分割成若干条链的形式,以维护树上路径的信息。
具体来说,将整棵树剖分为若干条链,使它组合成线性结构,然后用其他的数据结构维护信息。
——OI-WIKI
不知道大家在平时做题的时候会不会遇到这样一类问题:
-
将树从 \(x\) 到 \(y\) 结点的路径上所有节点的值都加上 \(z\) (树上路径加)。
其实可以树上差分
-
求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和(树上路径和)。
其实可以暴力,但是复杂度会炸
欸你有没有发现这种问题如果在序列或者线段上我们是不是很好做,直接线段树/树状数组。
但是在树上就不知道怎么解决了。
总结一下:
-
修改 树上两点之间的路径上 所有点的值。
-
查询 树上两点之间的路径上 节点权值的 和/极值/其它(在序列上可以用数据结构维护,便于合并的信息)。
——OI-WIKI
这类问题,我们就利用树剖转化为序列问题来处理。
二、结构&声明
研究一个数据结构或算法,我们也要追问自己为什么它是这样设计的,是根据什么性质,亦或是和什么有关联。上面我们说了我们面临着那样的问题才发明了重链剖分。那么我们思考一下怎么才能实现将树上问题转化成序列。
一种直接的想法是不是就是将它暴力分成很多条链,如下图。
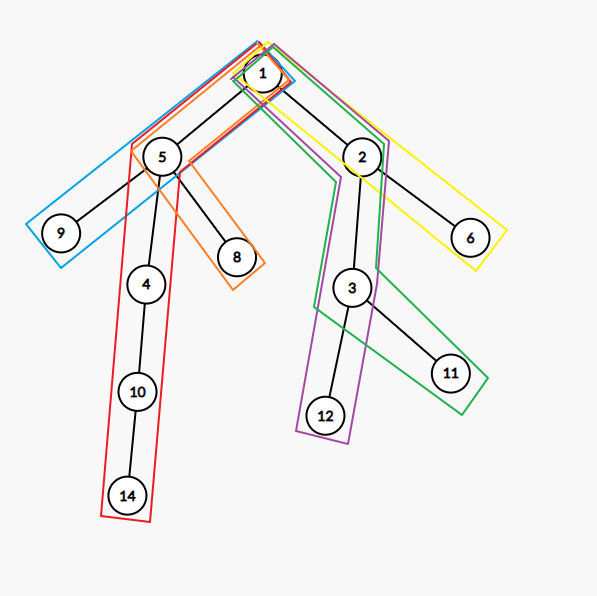
可是这种剖分方法会有重复节点,我们不好处理,所以我们要找到一种方法,将树不重不漏地剖成一些链,然后维护。于是重链剖分的方法就出现了。
为什么要将树分成重儿子、轻儿子,为什么要将其剖成重链呢(事实上,根据维护的问题不同,还有长链剖分、实链剖分等,但是这里只讨论重链剖分)?思考我们要剖成链,就要有一个优先,其他靠后,根据这个优先顺序来维护。和树上dsu相似的,一个结点的重儿子是最重要的,优先访问的。
如下图(来自OI-WIKI)
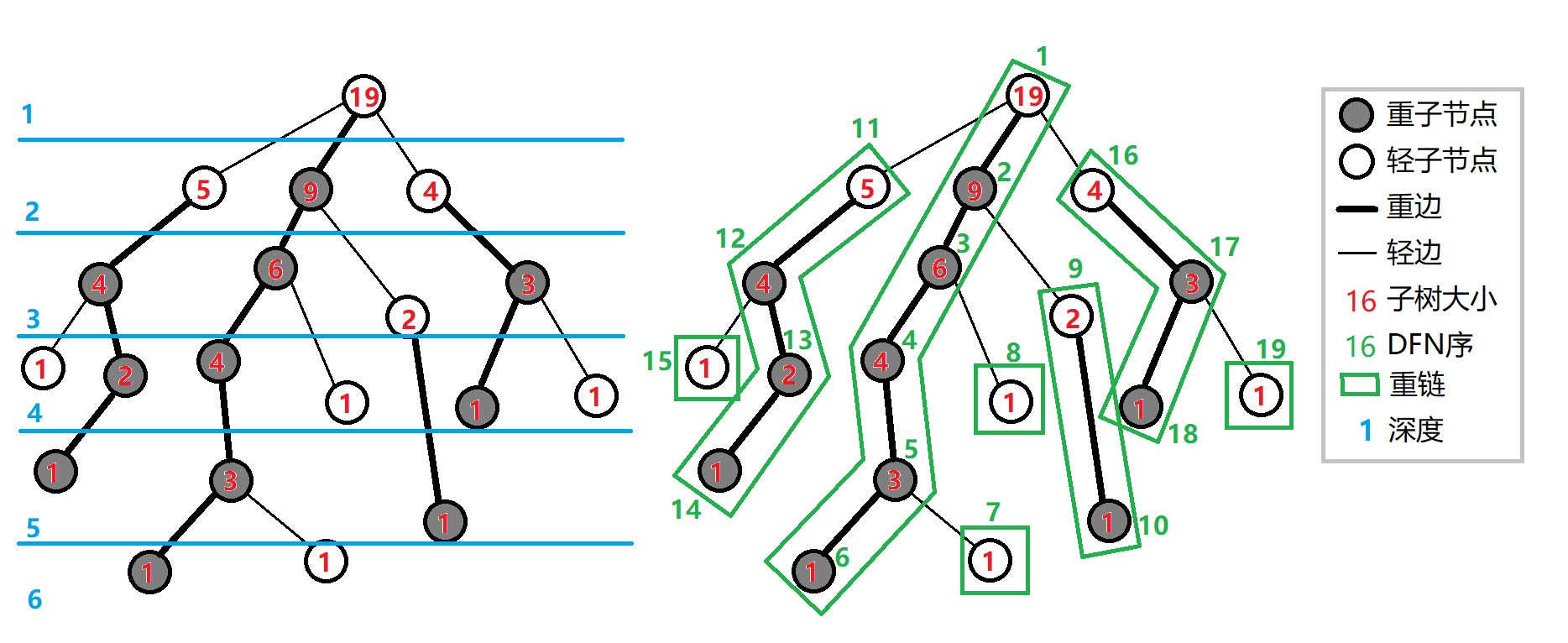
一些声明(在有根树中):
| 名词/变量 | 含义 | 名词/变量 | 含义 |
|---|---|---|---|
| 重儿子 | 所有儿子中子树大小最大的儿子 | 轻儿子 | 除了重儿子以外的其他儿子都是轻儿子 |
| 重边 | 从这个节点连到重子节点的边 | 轻边 | 从这个节点到其它子节点的边 |
| 重链 | 几条重边首尾相接得到的链,特别的,落单的节点也是重链 | \(top[N]\) | 存储这条重链的顶端 |
| \(val[N]\) | 剖分以后对应 \(dfn\) 序的点权 | \(sz[N]\) | 子树大小 |
| \(s[N]\) | 每个结点的重儿子 | \(f[N]\) | 每个结点的父节点 |
看不懂的先去看后面,这里只是给出参照,后面有解释。
其实看代码就行,都是很正常的变量名和定义。
三、重链剖分的原理和实现
先来谈谈重链剖分的性质:
- 树上每个节点都属于且仅属于一条重链。
- 所有的重链将整棵树完全剖分。
- 在剖分时重边优先遍历。
这三条算是重申。
- 由 3 得 最后树的 DFS 序上,重链内的 DFS 序是连续的。按 \(dfn\) 排序后的序列即为剖分后的链。
这一句是重点,揭示了原理。
- 当我们向下经过一条轻边时,所在子树的大小至少会除以二,即如果 \((u,v)\) 是一条轻边,那么 \(sz[v]<sz[u]/2\)。所以对于树上的任意一条路径,把它拆分成从 LCA 分别向两边往下走,分别最多走 \(O(\log n)\) 次,因此,树上的每条路径都可以被拆分成不超过 \(O(\log n)\) 条重链。即从根结点到任意结点的路所经过的轻重链的个数必定都小于 \(O(\log n)\) 。
这一点通常用于时间复杂度证明。
那么我们怎么实现这一点呢?
首先我们要得到上面那些数组的值,这部分可以用两个 \(dfs\) 预处理。
在 \(dfs1\) 处理 \(sz\),\(f\),\(s\),\(dep\) 这四个数组。没什么好说的。
inline void init1(int nw,int fa){f[nw]=fa;dep[nw]=dep[fa]+1,sz[nw]=1;for(int i=hd[nw];i;i=e[i].nxt){if(fa!=e[i].to){init1(e[i].to,nw);sz[nw]+=sz[e[i].to];if(sz[e[i].to]>sz[s[nw]]) s[nw]=e[i].to;}}
}
在 \(dfs2\) 将各个重结点连成重链,处理出 \(dfn\),(因为上一次 \(dfs1\) 以后才知道重儿子,才能确定访问顺序),以及当前节点所在链的起点(\(top\)),还有对应 \(dfn\) 上的权值。
inline void init2(int nw,int fa){dfn[nw]=++idx;val[idx]=v[nw];top[nw]=fa;if(!s[nw]) return;init2(s[nw],fa);for(int i=hd[nw];i;i=e[i].nxt){if(e[i].to!=f[nw]&&e[i].to!=s[nw]) init2(e[i].to,e[i].to);//轻链的开头是自己}
}
比较难的就是我们怎么把这些信息整合得到我们所需要的,在下面具体运用时讲吧。
将重链(对应 \(dfn\) 一段区间)用树状数组/线段树来进行维护(这里就选择线段树了,因为不需要动脑子)
可以看看 OI-WIKI 的伪代码。
四、应用
1. 求LCA
求LCA有倍增法,是在暴力跳父亲的方法上进行了优化,那么我们来考虑树剖如何优化跳父亲。
既然树被我们剖成了若干链,那LCA就有两种情况:1.同一链上两个节点求LCA,2.不同链上求LCA
第一种显然是深度较浅的,判断方法就是看top
第二种不同链则一定是LCA分叉,分成了重链和轻链,我们不是记了top吗,可以用top直接跳过一条链来加速。
但是一个问题是可能会跳过LCA,比如一个点在另一个点分叉的上方,如果无脑跳就跳过去了。我们要仔细考虑一下如何跳top。
考虑我们的目的就是让两个点跳到同一条链上,所以每次选择top深度较深的那个点跳,如果在同一条链上就结束啦。
可以证明单次查询时间复杂度 \(O(\log n)\)。
注意每次跳一整个链,所以跳到 \(f[top[v]]\)。
理解 lca 是理解后面路径查修的基础,要看动态演示可以去看董晓算法的图(可能不用)。
inline int lca(int u,int v){while(top[u]!=top[v]){if(dep[top[u]]>dep[top[v]]) swap(u,v);v=f[top[v]];}return dep[u]<dep[v]?u:v;
}
2. 子树修改查询。
这个和正常的一样,因为子树内 \(dfn\) 连续,所以记录子树内最大最小的 \(dfn\) ,其实就是正常线段树维护 \(dfn[u]\sim dfn[u+sz[u]-1]\) 这个区间即可。
Modify(1,dfn[u],dfn[u]+sz[u]-1,x);Query(1,dfn[u],dfn[u]+sz[u]-1)%mod);
3. 路径修改查询。
树上路径 \((u,v) \rightarrow (u,lca)+(lca,v)\),剖成重链以后我们可以将其分为两段:向上跳 \(lca\) 的一段和最后较深的点向较浅的点靠。由于前面说过,通过重链剖分的形式保证了一条链上的 \(dfn\) 序是连续的,所以这两段我们可以将其放到线段树上,在 \(val\) 数组中求区间和。过程中的范围是 \(dfn[{top_u}]\sim dfn[u]\) 设跳到最后较深的点是 \(ed\),则范围是 \(dfn[lca]\sim dfn[ed]\)。
inline long long Path_qry(int u,int v){long long ans=0;while(top[u]!=top[v]){if(dep[top[u]]>dep[top[v]])swap(u,v);ans=(ans+Query(1,dfn[top[v]],dfn[v]))%mod;v=f[top[v]]; }if(dep[u]>dep[v])swap(u,v);ans=(ans+Query(1,dfn[u],dfn[v]))%mod;return ans;
}inline void Path_mdf(int u,int v,int k){while(top[u]!=top[v]){if(dep[top[u]]>dep[top[v]]) swap(u,v);Modify(1,dfn[top[v]],dfn[v],k);v=f[top[v]]; }if(dep[u]>dep[v])swap(u,v);Modify(1,dfn[u],dfn[v],k);return;
}
所有程序
#include<bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
using namespace std;
const int N=1e5+5;
int n,m,rt,q,mod;
struct E{int to,nxt;
}e[N<<1];int tot,hd[N];
int idx,f[N],v[N],val[N],dep[N];
struct Tr{int l,r;ll val,tag;
}tr[N<<2];
int sz[N],s[N],dfn[N],top[N];
inline int read(){char ch;int x=0,f=1;while(!isdigit(ch=getchar())){if(ch=='-') f=-1;}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;
}
inline void Build(const int p,const int l,const int r){tr[p].l=l,tr[p].r=r,tr[p].val=val[r];if(l==r){tr[p].val=val[l]%mod;return;}int mid=(l+r)>>1;Build(ls,l,mid);Build(rs,mid+1,r);tr[p].val=(tr[ls].val+tr[rs].val)%mod;return;
}
inline void Add(int u,int v){++tot,e[tot].to=v;e[tot].nxt=hd[u],hd[u]=tot;
}
inline void init1(int nw,int fa){f[nw]=fa;dep[nw]=dep[fa]+1,sz[nw]=1;for(int i=hd[nw];i;i=e[i].nxt){if(fa!=e[i].to){init1(e[i].to,nw);sz[nw]+=sz[e[i].to];if(sz[e[i].to]>sz[s[nw]]) s[nw]=e[i].to;}}
}
inline void init2(int nw,int fa){dfn[nw]=++idx;val[idx]=v[nw];top[nw]=fa;if(!s[nw]) return;init2(s[nw],fa);for(int i=hd[nw];i;i=e[i].nxt){if(e[i].to!=f[nw]&&e[i].to!=s[nw]){init2(e[i].to,e[i].to);//轻链的开头是自己}}
}
inline int lca(int u,int v){while(top[u]!=top[v]){if(dep[top[u]]>dep[top[v]]) swap(u,v);v=f[top[v]];}return dep[u]<dep[v]?u:v;
}
inline void Change(const int p,const int val){tr[p].val=(tr[p].val+val*(tr[p].r-tr[p].l+1)%mod)%mod;tr[p].tag=(tr[p].tag+val)%mod;return;
}
inline void Pushdown(const int p){if(!tr[p].tag) return;Change(ls,tr[p].tag);Change(rs,tr[p].tag);tr[p].tag=0;return;
}
inline long long Query(const int p,const int l,const int r){if(tr[p].l>=l&&tr[p].r<=r) return tr[p].val;Pushdown(p);int mid=(tr[p].l+tr[p].r)>>1;ll ans=0;if(l<=mid) ans+=Query(ls,l,r);if(mid<r) ans=(ans+Query(rs,l,r))%mod;return ans;
}
inline long long Path_qry(int u,int v){long long ans=0;while(top[u]!=top[v]){if(dep[top[u]]>dep[top[v]])swap(u,v);ans=(ans+Query(1,dfn[top[v]],dfn[v]))%mod;v=f[top[v]]; }if(dep[u]>dep[v])swap(u,v);ans=(ans+Query(1,dfn[u],dfn[v]))%mod;return ans;
}
inline void Modify(const int p,const int l,const int r,const int k){if(tr[p].l>=l&&tr[p].r<=r){tr[p].val=(tr[p].val+k*(tr[p].r-tr[p].l+1)%mod)%mod;tr[p].tag=(tr[p].tag+k)%mod;return;}Pushdown(p);int mid=(tr[p].l+tr[p].r)>>1;if(l<=mid) Modify(ls,l,r,k);if(mid<r) Modify(rs,l,r,k);tr[p].val=(tr[ls].val+tr[rs].val)%mod;return;
}
inline void Path_mdf(int u,int v,int k){while(top[u]!=top[v]){if(dep[top[u]]>dep[top[v]]) swap(u,v);Modify(1,dfn[top[v]],dfn[v],k);v=f[top[v]]; }if(dep[u]>dep[v])swap(u,v);Modify(1,dfn[u],dfn[v],k);return;
}
int main(){n=read(),m=read(),rt=read(),mod=read(),q=read();for(int i=1;i<=n;++i) v[i]=read();int u,v,x;for(int i=1;i<n;++i){u=read(),v=read();Add(u,v),Add(v,u);}init1(rt,0),init2(rt,rt);Build(1,1,n);while(m--){u=read();if(u==1){u=read(),v=read(),x=read();Path_mdf(u,v,x);}else if(u==2){u=read(),v=read();printf("%lld\n",Path_qry(u,v)%mod);}else if(u==3){u=read(),x=read();Modify(1,dfn[u],dfn[u]+sz[u]-1,x);}else{u=read();printf("%lld\n",Query(1,dfn[u],dfn[u]+sz[u]-1)%mod);}}while(q--){u=read(),v=read();printf("%d\n",lca(u,v));}return 0;
}
五、练习
P3384 【模板】重链剖分/树链剖分
待补
参考 (虽然没有看) :
树链剖分 - OI Wiki
树链剖分学习笔记 - l_x_y - 博客园
树链剖分详解 - Ivanovcraft - 博客园
算法学习笔记() DFS序、树链剖分及其应用_dfs序的应用-CSDN博客
树链剖分良心讲解 - 洛谷专栏
树链剖分详解(洛谷模板 P3384) - ChinHhh - 博客园
P3384 【模板】重链剖分/树链剖分 - 洛谷
算法学习笔记:树链剖分-CSDN博客
董晓算法 D12 Luogu P3384【模板】轻重链剖分/树链剖分
好多啊
可以看看一些别的类似问题(不是重链剖分),如 K-father and K-son
写完这篇学习笔记的时候正好放学了,郊眠寺正唱到结尾,我又重新拾起来希望,像拾起秋天里一支破败的枯枝。