20240914 模拟赛
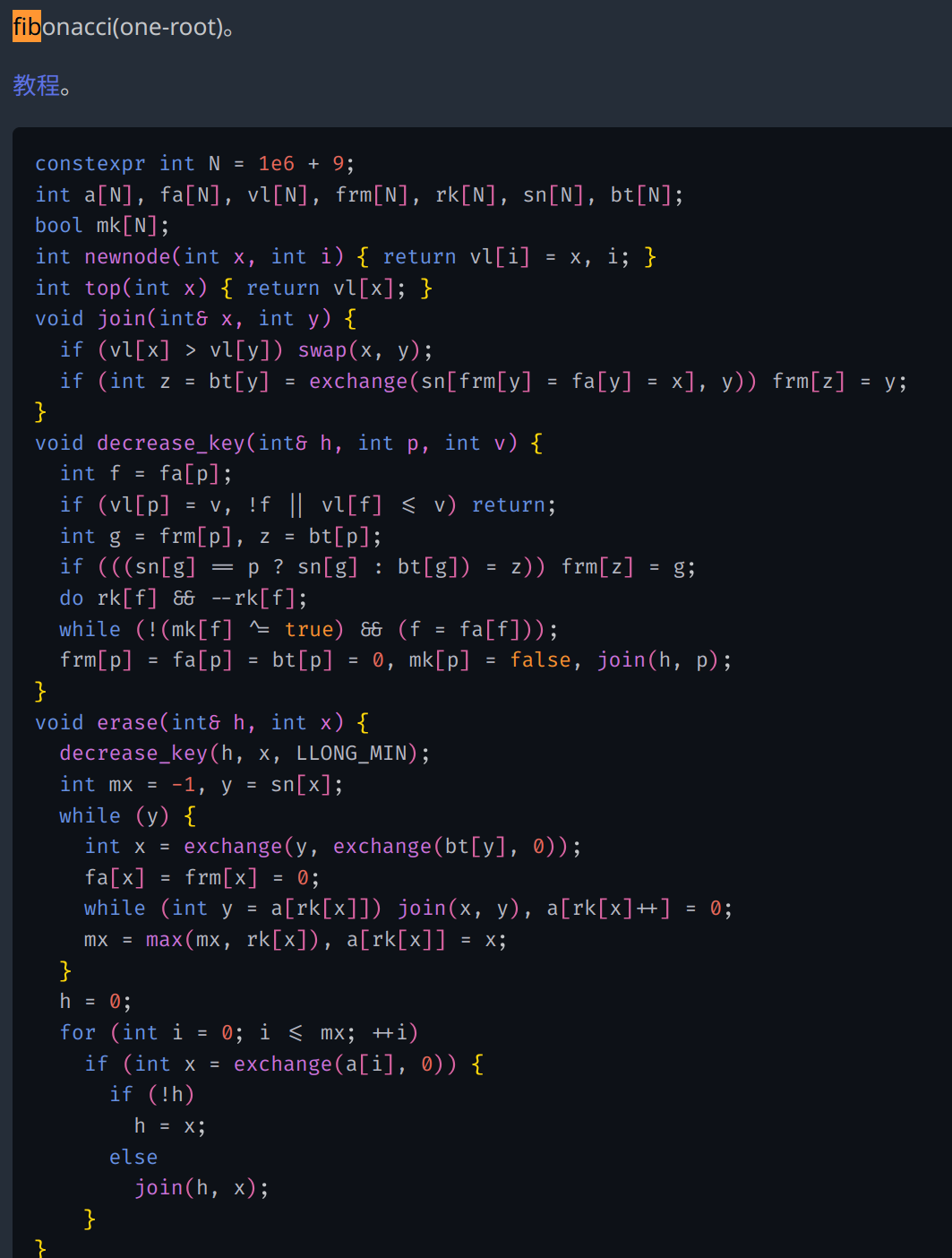
A 开挂(openhook)
可以发现结果序列是能确定的,而且我们并不关心具体对哪个数进行操作,有用的信息只有操作次数,从而可以得到一个数组 \(c\) 表示对某个数操作了某个次数。设对 \(tot\) 个数进行了操作,将 \(c\) 从小到大排序,将 \(b\) 中的前 \(tot\) 小从大到小排序,于是 \(ans=\sum_{i=1}^{tot}c_ib_i\)。
要最小化这个值,注意到 \(c_i\) 的和是一定的,那么肯定是让较大的数越大越好,也就是尽可能不平均。考虑从原数组中取出一个最大的不重集合并排序,那么剩下的数要么插入集合中的两个数之间,要么放到末尾。放到末尾的部分容易处理,只需求出插入的情况。按值从小到大枚举这个集合中可插入的区间,根据分析的性质发现插入的数原本要越大越好,并且从大到小插入。二分出可插入的数,链表维护剩下的数就好,时间复杂度 \(O(n \log n)\)。
B 叁仟柒佰万(clods)
容易注意到一个性质,分开后每段的 \(mex\) 一定为全局 \(mex\),因为每个出现过的数都会使某一段的 \(mex\) 不为这个数。于是可以想到双指针维护哪些区间的 \(mex\) 为全局 \(mex\),时间复杂度 \(O(n)\)。
瞪眼可以想到一个 dp,设 \(f_{i,j}\) 表示前 \(i\) 个数分 \(j\) 段的方案数,这是 \(O(n^3)\) 的。很快发现记录段数根本没用,于是省掉第二维变成 \(O(n^2)\)。于是得到这样的式子:f[i] += f[l - 1] * check(l, i);,根据双指针的预处理可以 \(O(1)\) check。
分析得到能产生贡献的总是一段前缀,前缀和优化即可做到 \(O(n)\)。
这题卡空间,只能开 3 个 37000000 的 int 数组,把 \(f\) 省去即可。