基本概念
哈希和树一样,是数据库系统中用于访问数据的方法。

空间复杂度:$O(n)$
时间复杂度:$O(1)~ O(n)$
权衡:更大的哈希空间(碰撞减少),还是更少的哈希空间(碰撞处理)?
哈希函数
-
CRC-64(1975)
-
MurmurHash (2008)
-
Google CityHash (2011)
-
Facebook XXHash (2012) 【最常用】
-
Google FarmHash (2014)
哈希结构
两种思路:
- Operating Address【空间换时间】
- Linear Probe Hashing
- Cuckoo Hashing
- Chained Hashing(Bucket)【时间换空间】
- 结合(渐进式扩展哈希空间)
- Extenible Hashing
- Linear Hashing【最常用】
下面探讨如何通过这些机制避免或处理哈希值碰撞。
Linear Probe Hashing
-
碰撞时移动到下一个槽
-
删除时建立墓碑:墓碑可以被新值代替;也可以通过垃圾回收清理
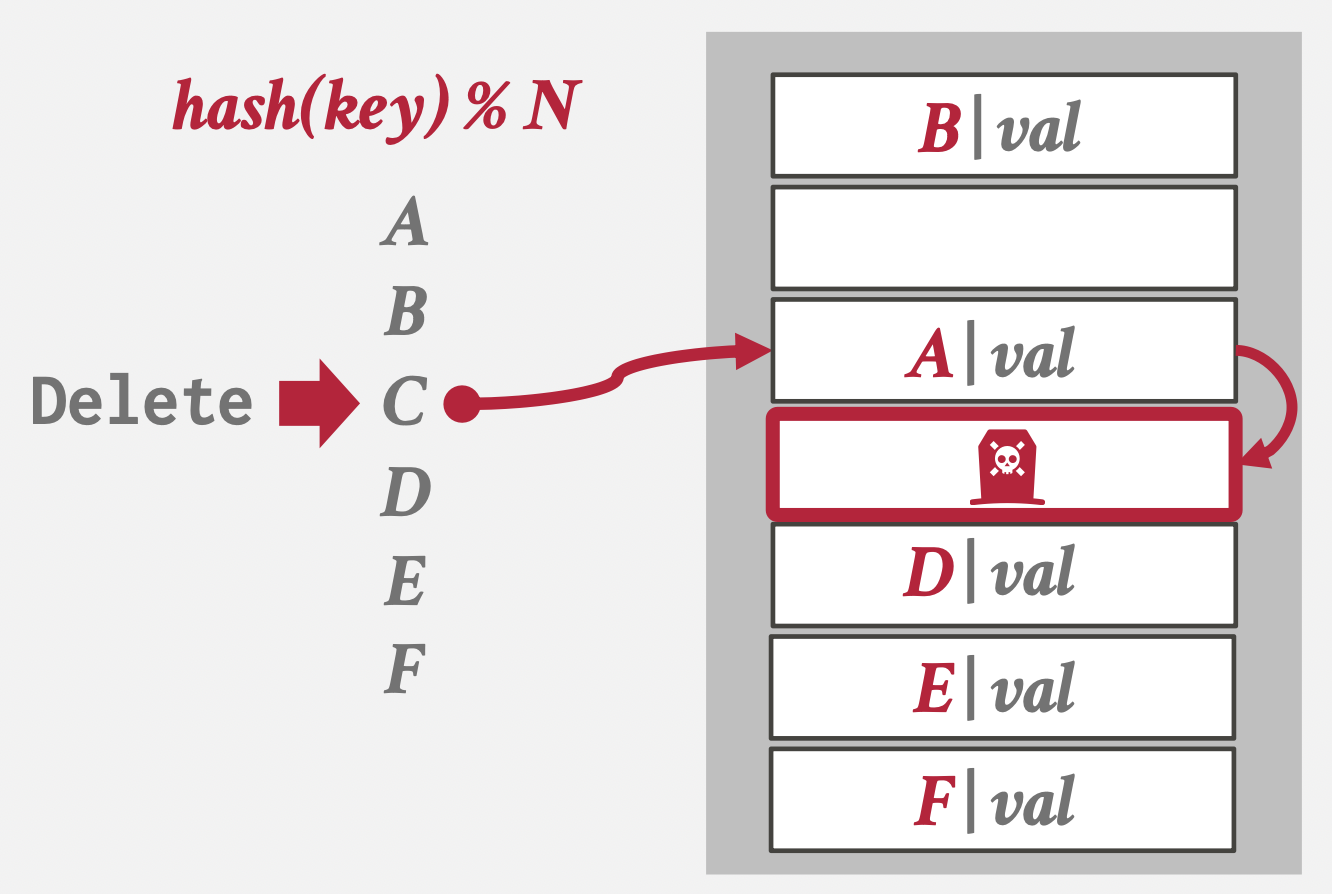
-
非唯一值怎么存:键值同存(如上图所示,每个槽里存放的是键和值)
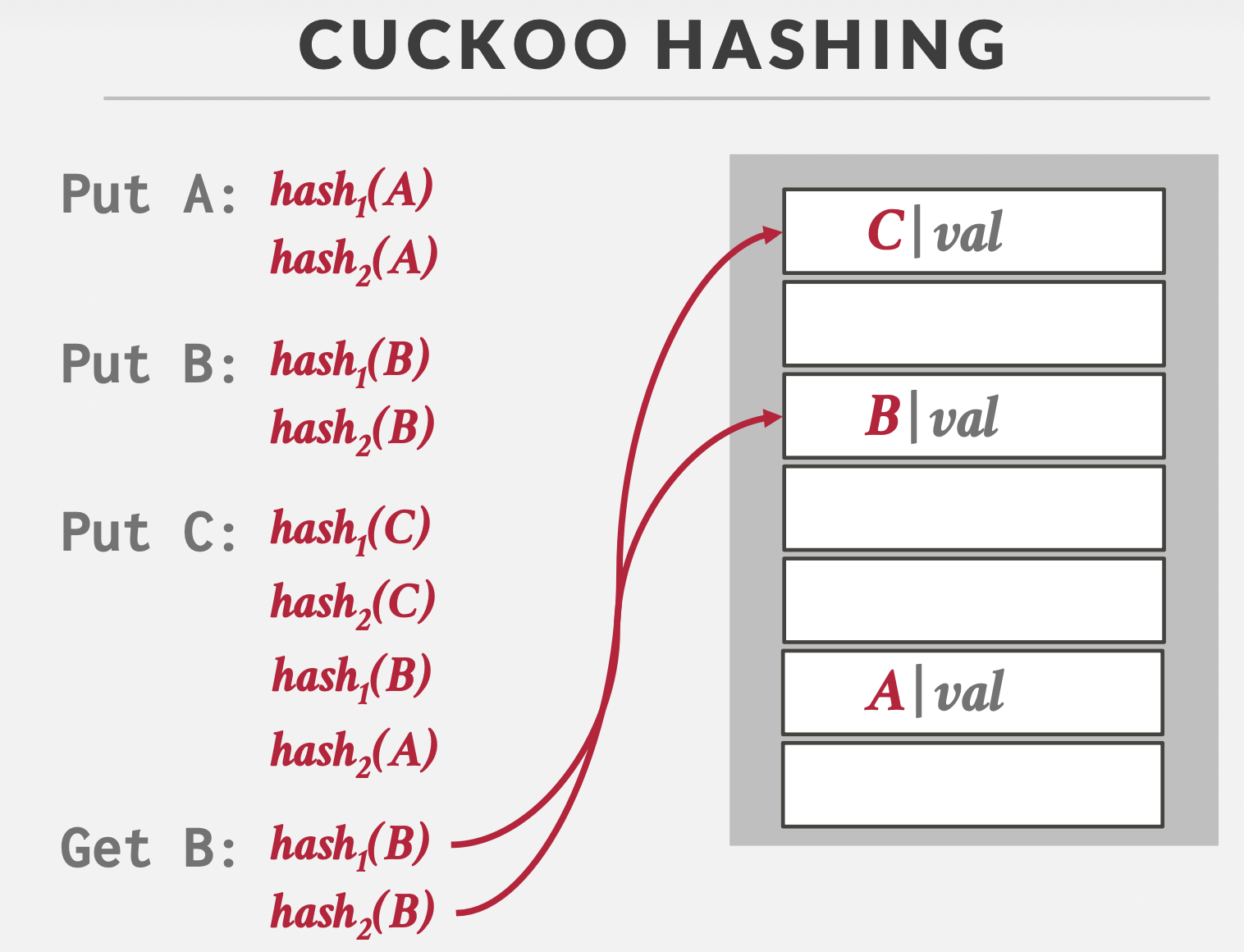
Cuckoo Hashing
-
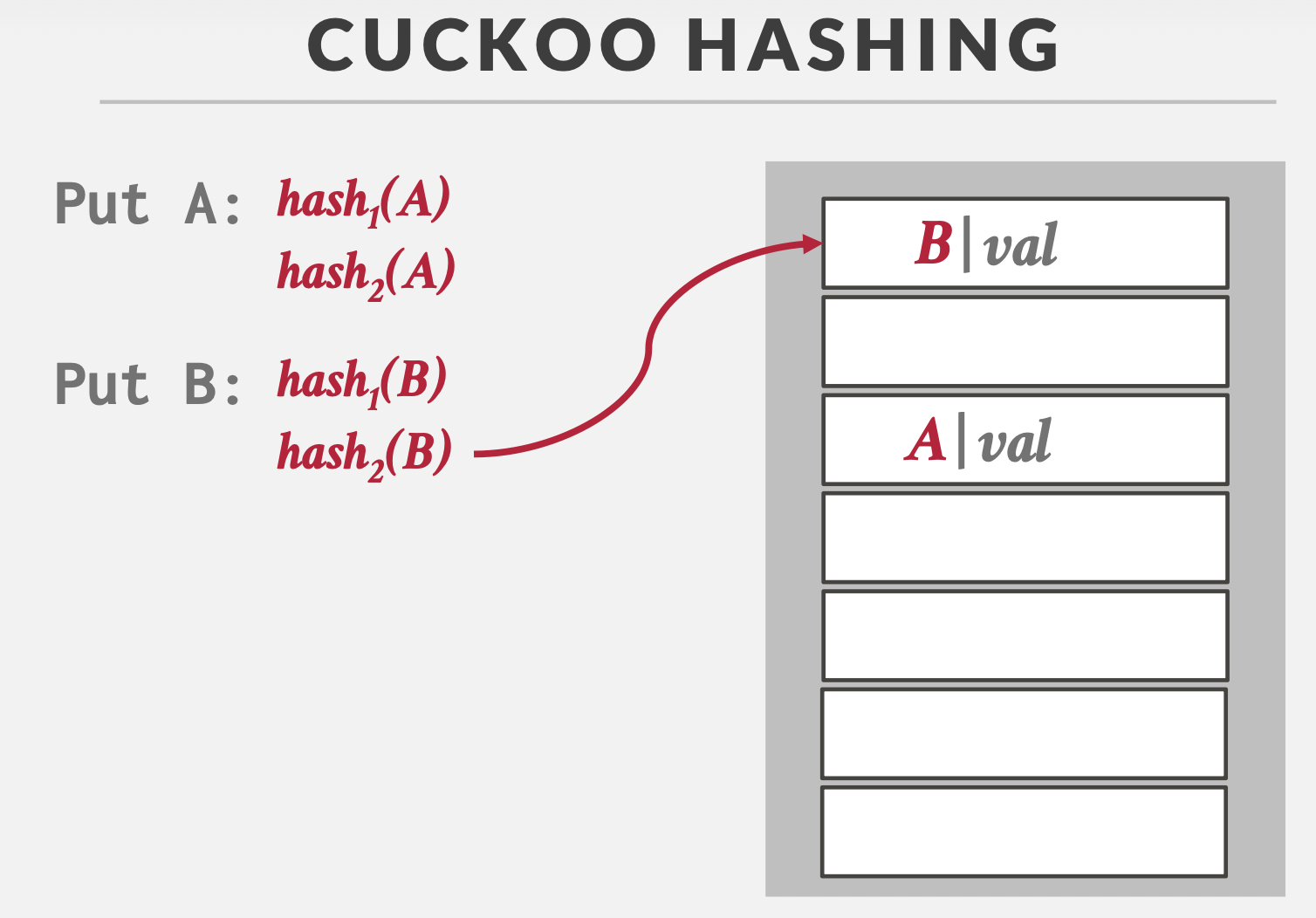
基本思想:多哈希函数+鸠占鹊巢
-
注意点:无限循环检测
过程演示:
有空位时:直接占用。
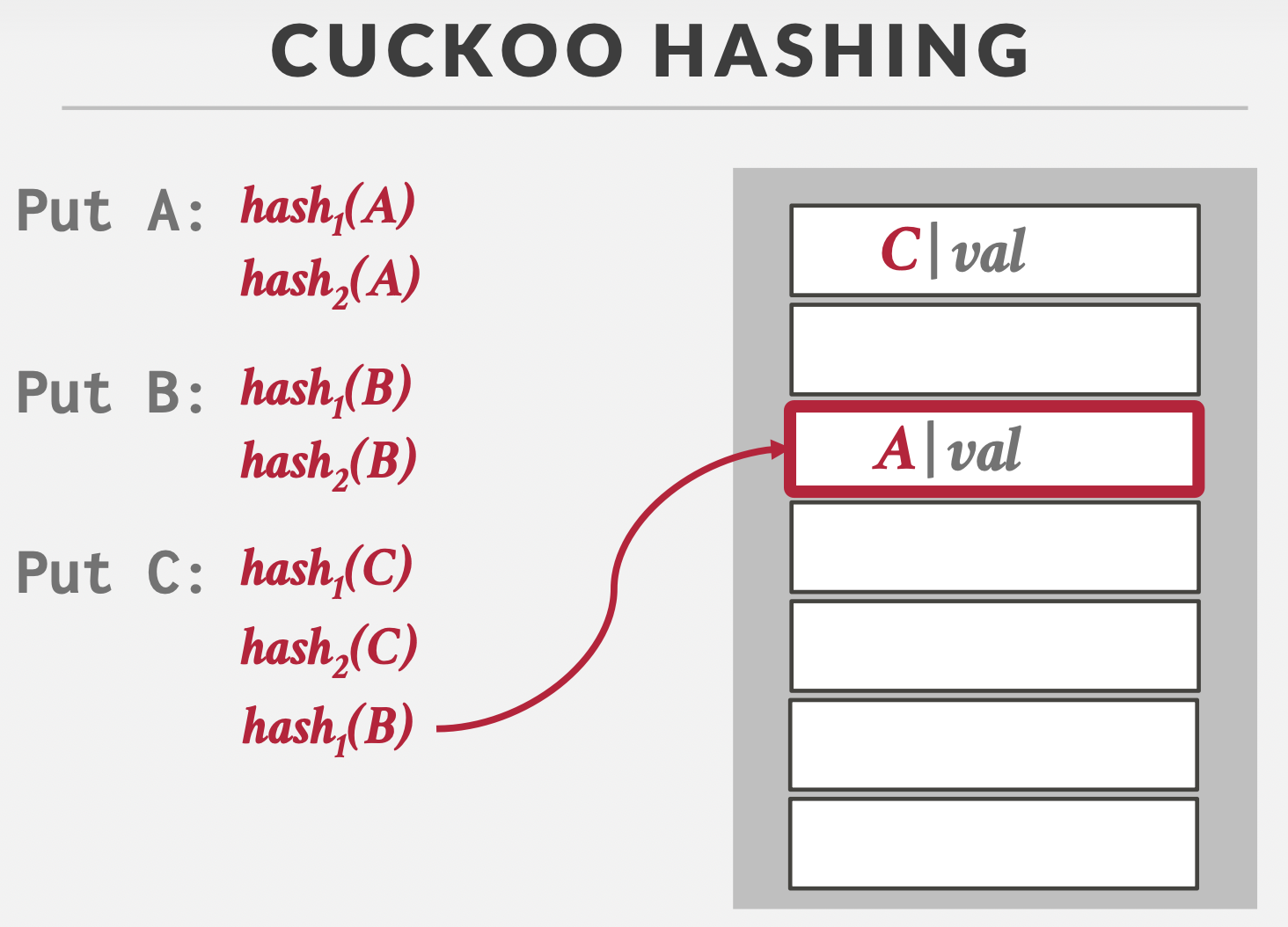
发生碰撞时,如果两个哈希位都已经被占用了,踢出原来的数据,让他重新哈希,以此反复,直到找到空位。
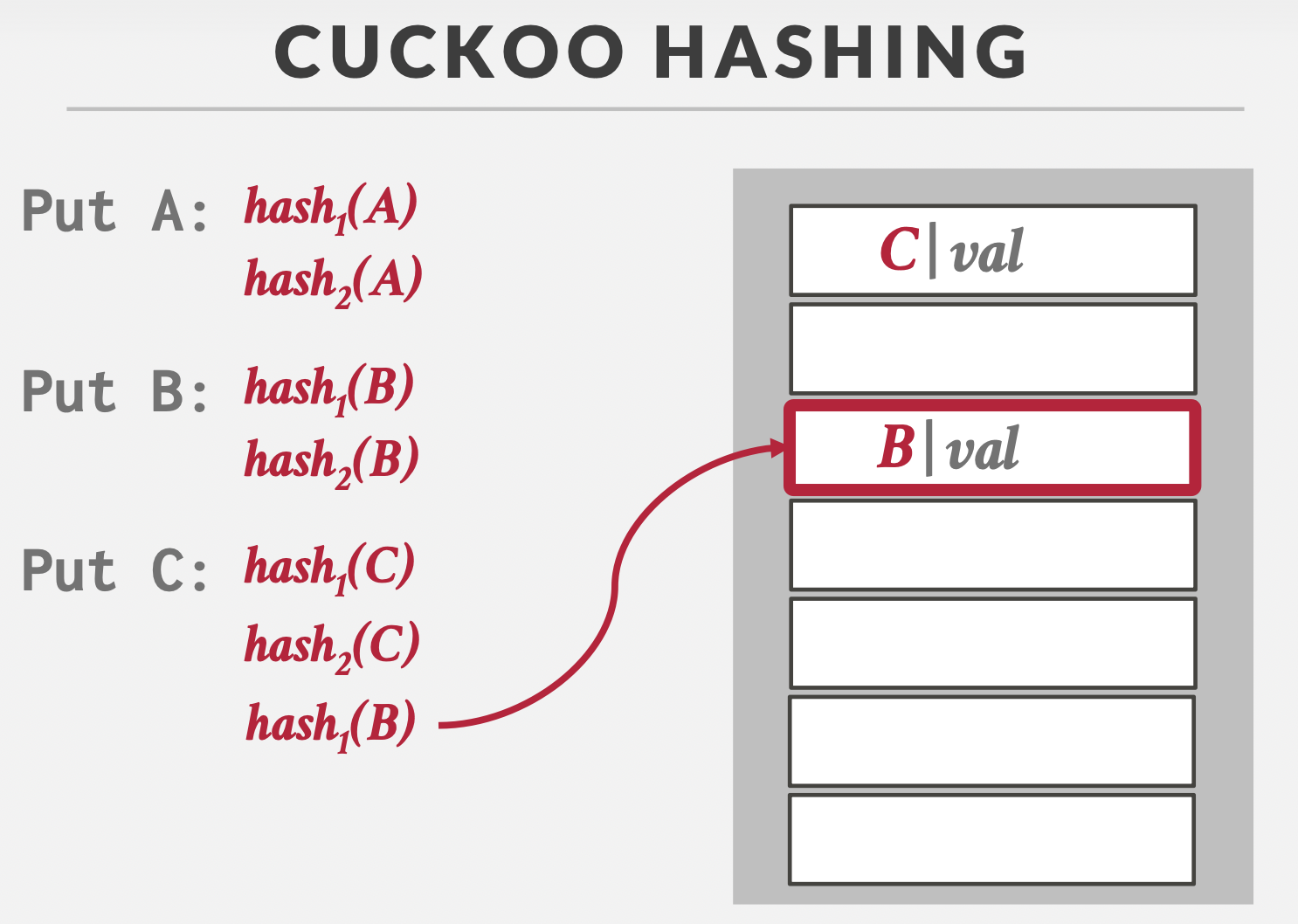

获取时只需要找两个哈希位即可。
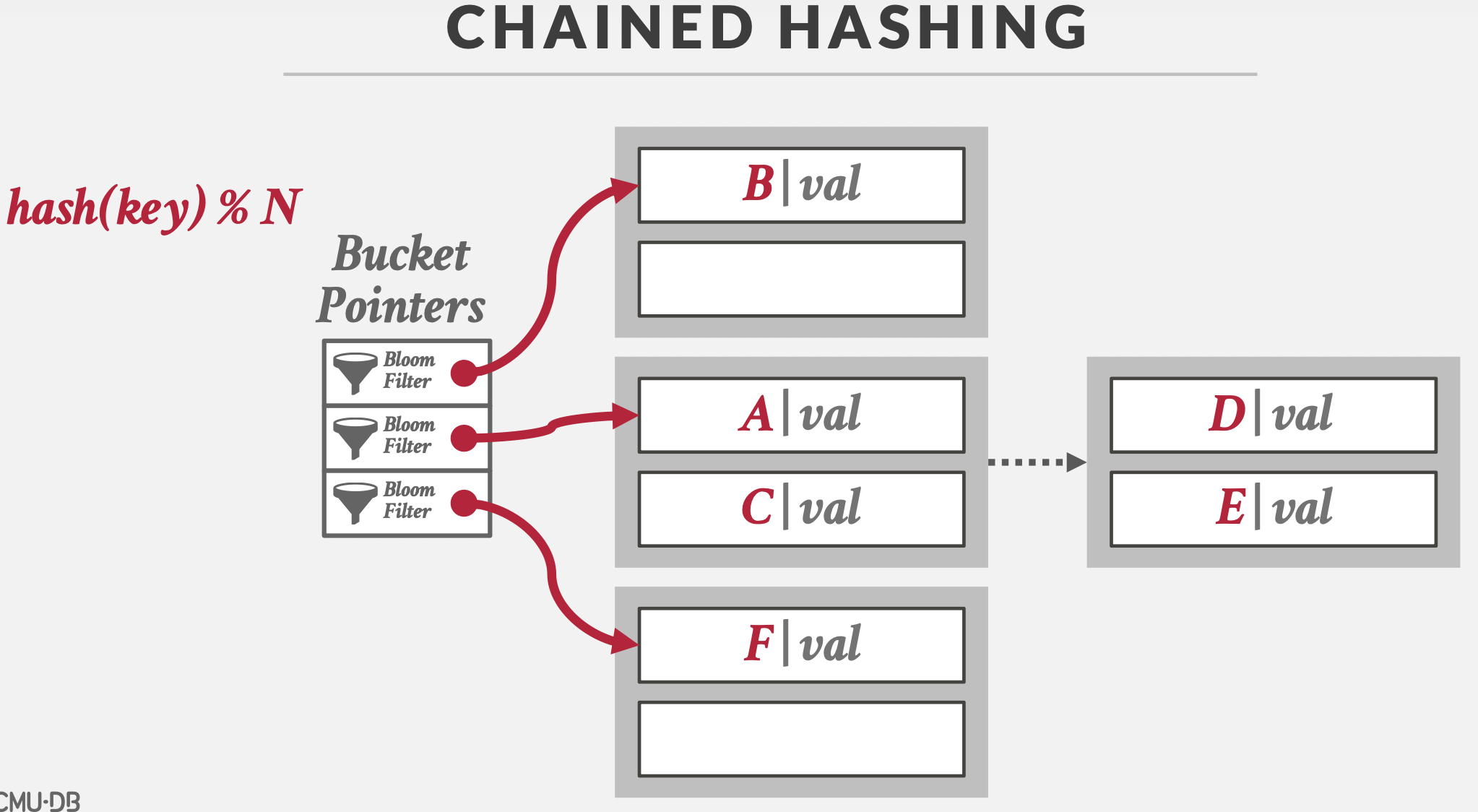
Chained Hashing
- 碰撞数据存在哈希桶中,桶满则溢出
- 布隆过滤器加速查询
Extenible Hashing
依照哈希值的位映射到哈希桶。
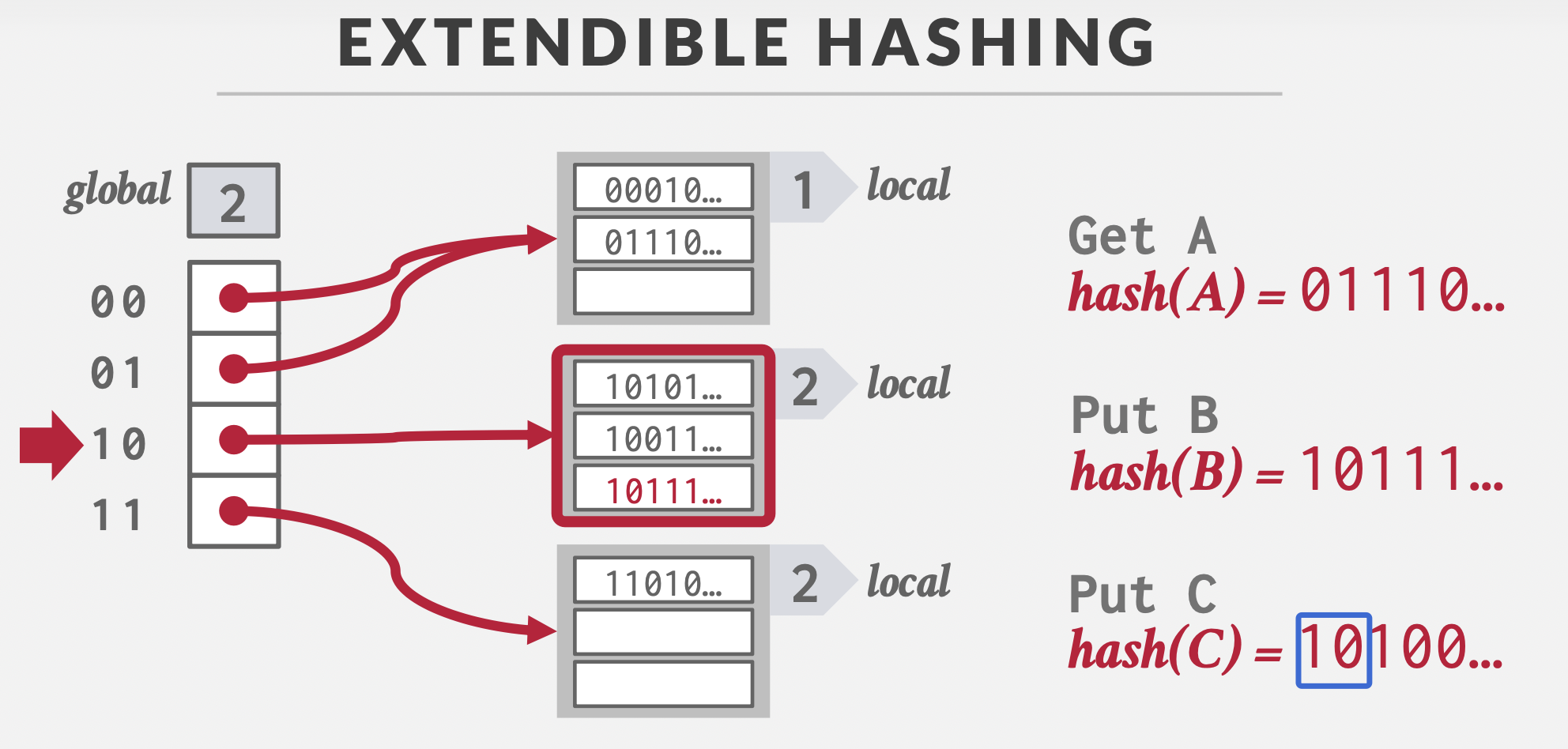
00和01指向同一个桶是因为复用。
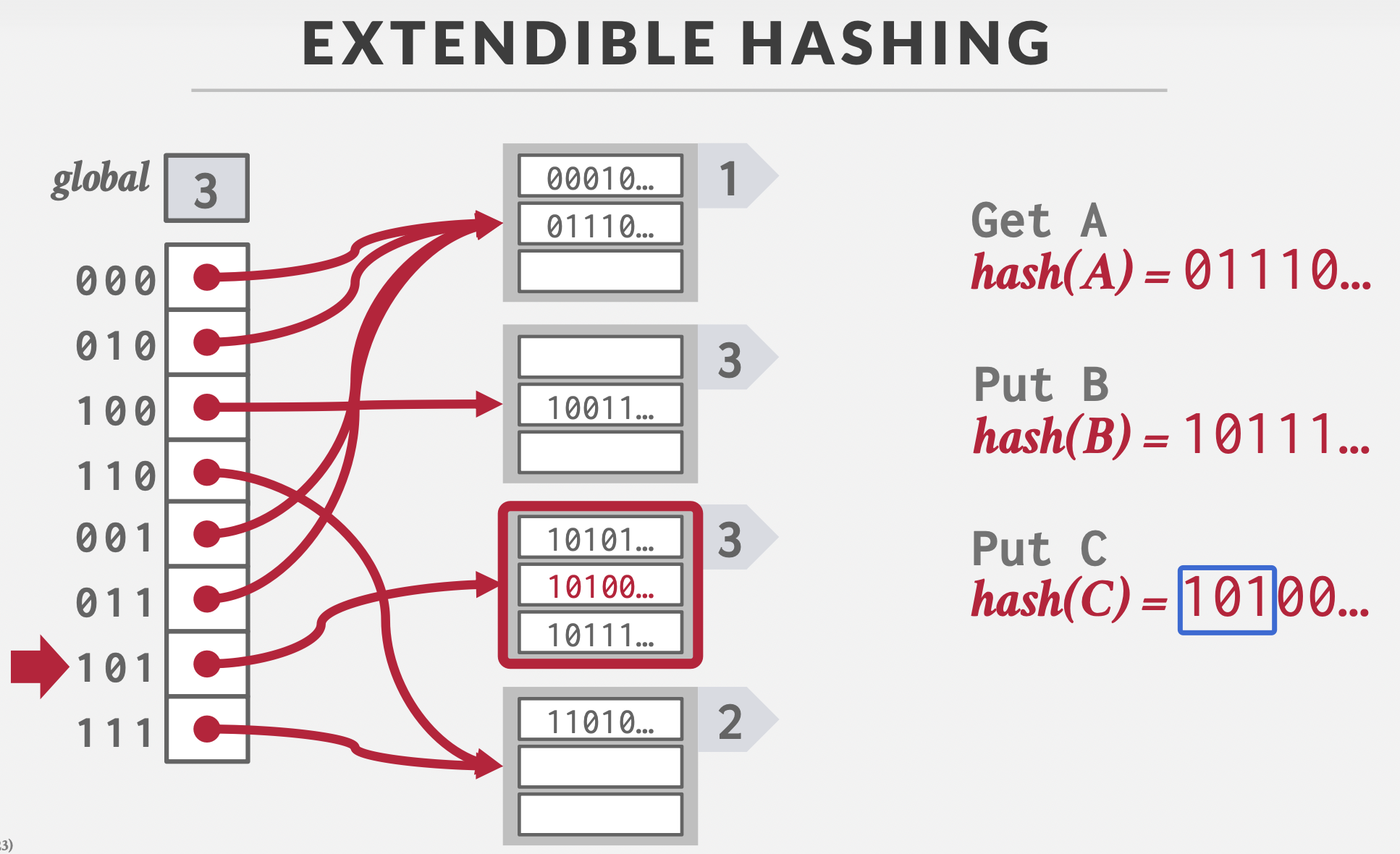
插入C时,对应的哈希桶10已经满了,选择位增加为3,拓展10的哈希空间为100和101,移动数据,尝试插入。
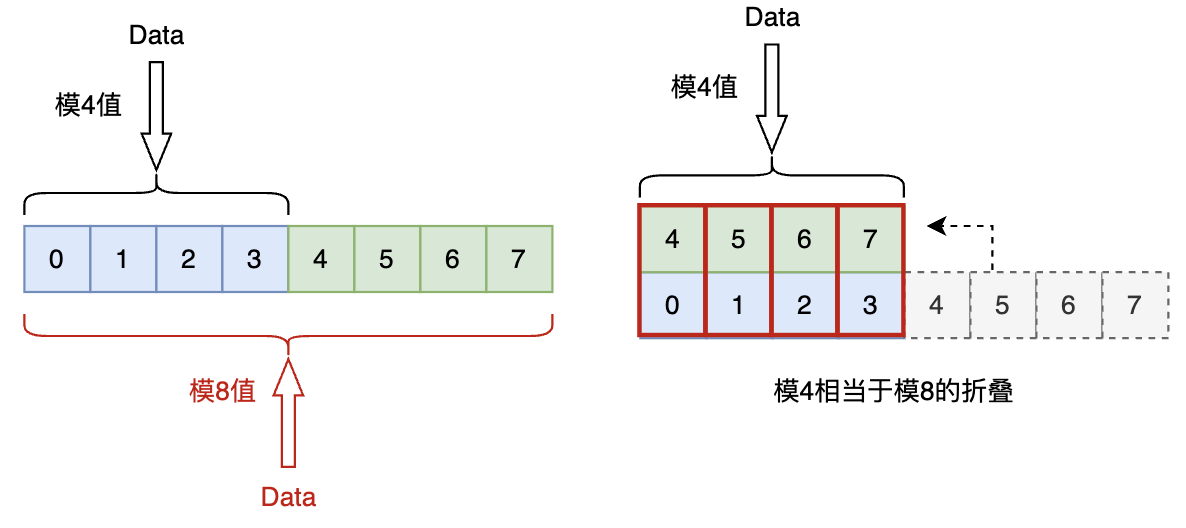
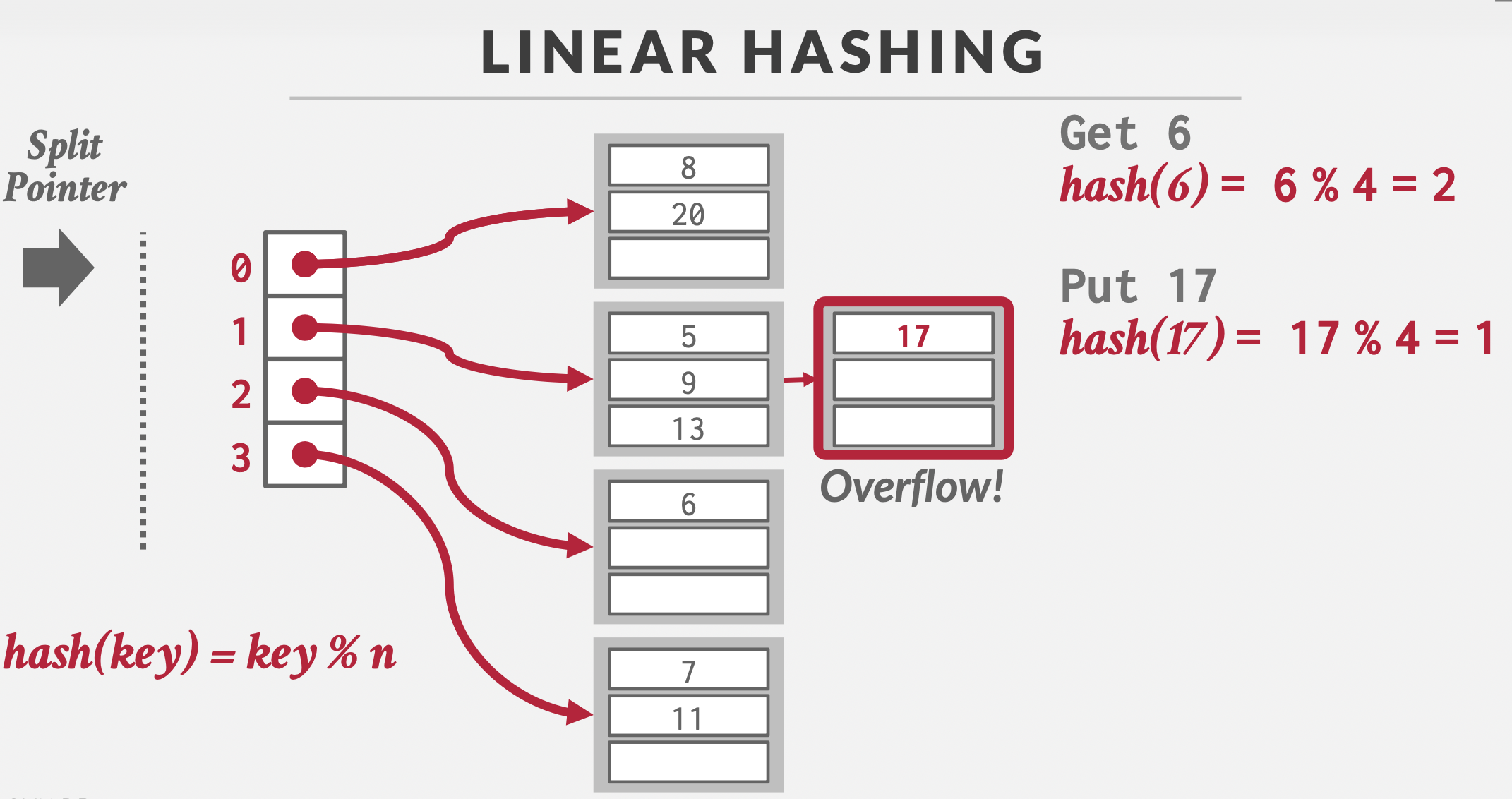
Linear Hashing
基本思想:
-
渐进式扩展:当哈希桶溢出时,不是分裂溢出的哈希桶,分裂指针指向的哈希桶,渐进地扩充所有哈希桶。
-
循环扩展:当本轮所有哈希桶都分裂完后,指针跳转回起始位置,重新开始循环,并丢弃上一轮的哈希函数。
-
查询保证:查找一个数据最多只会有两次哈希。
过程演示:
插入17时,1号哈希桶溢出,扩展0号哈希桶,分裂指针下移;数据8和20对8取模做数据重分布。
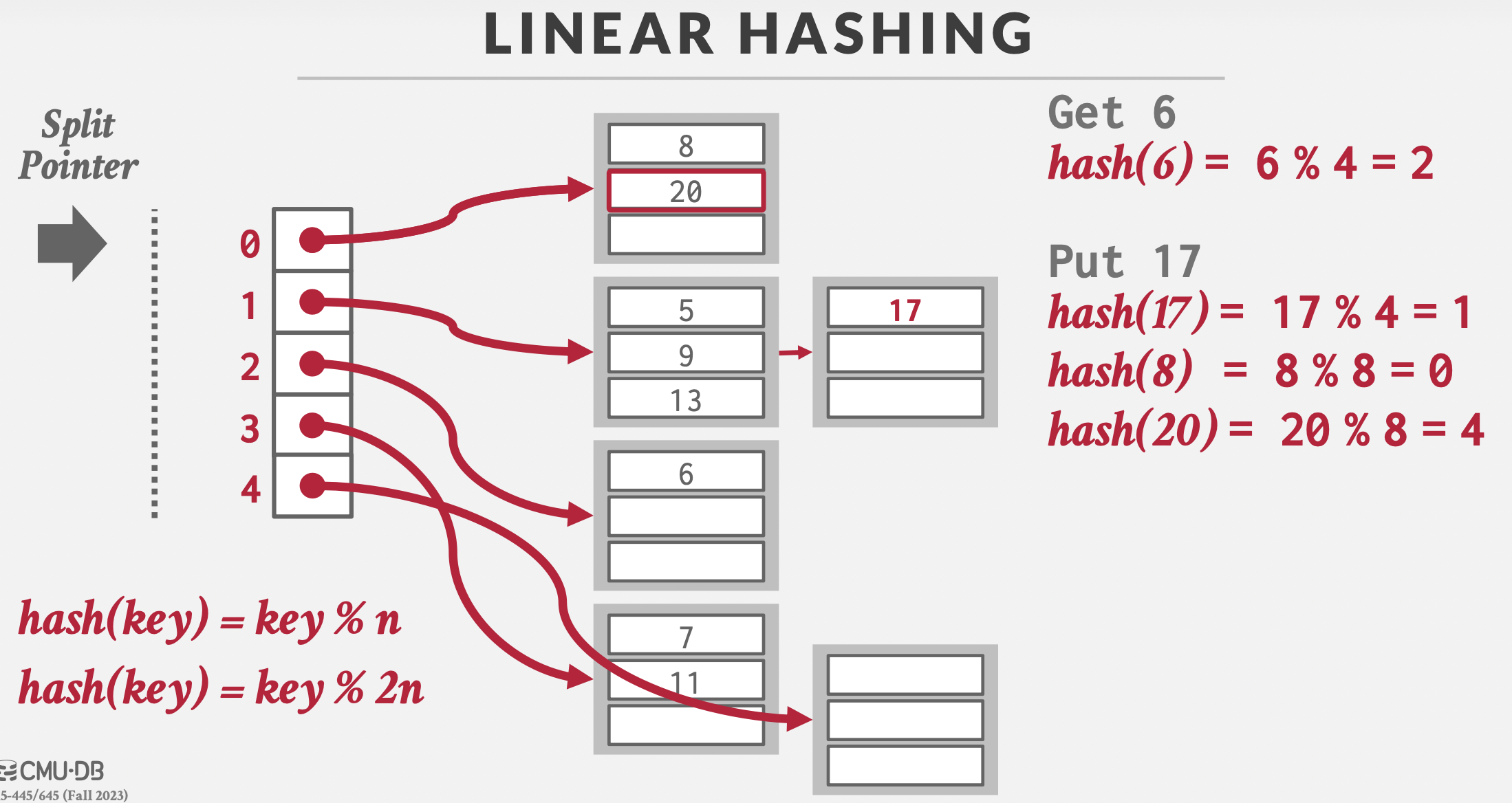
查询值20时,对4取模,落到0号桶,由于在分裂指针上方,说明需要再次对8(2n)取模,落到4号桶内,查询得到值20。
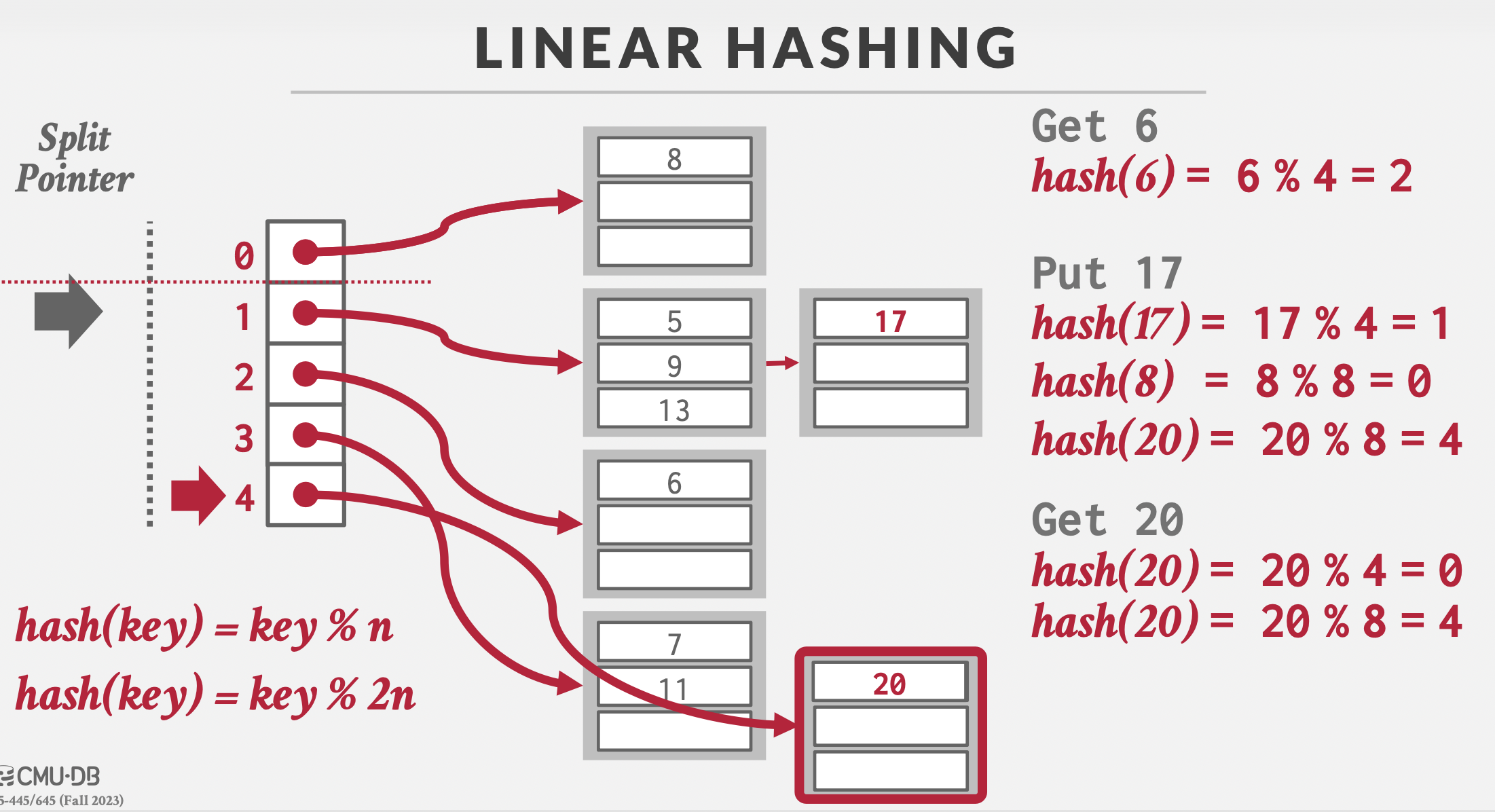
垃圾回收:如果最末位的哈希桶为空,可以删除,然后上移分裂指针。
分裂指针走到哪里跳回开头,不会无限循环吗:有变量记录当前轮的截止位置,避免无限循环。
为什么在0号桶对4取模后,再对8取模,得到的结果只会在0和4号桶,而不会到其他比如5,6,7号桶:见下图。