2024-2025-1 20241325 《计算机程序与设计》第七周学习总结
这个作业属于的课程<2024-2025-1-计算机基础与程序设计](https://edu.cnblogs.com/campus/besti/2024-2025-1-CFAP)>
这个作业要求在哪里:https://www.cnblogs.com/rocedu/p/9577842.html#WEEK07
这个作业的目标:
这个作业在哪里:https://www.cnblogs.com/wangxianglong999/p/18538299
- 数组与链表
- 基于数组和基于链表实现数据结构
- 无序表与有序表
- 树
- 图
- 子程序与参数
教材学习内容总结
数组和链表
数组和链表是两种常见的数据结构,它们在存储方式、访问方式、插入和删除操作等方面存在一些不同。
一、存储方式
-
数组
- 数组是一块连续的内存空间,用于存储相同类型的数据元素。
- 例如,一个整数数组在内存中是连续存放的一系列整数。
-
链表
- 链表是由一系列节点组成,每个节点包含数据和指向下一个节点的指针(在双向链表中还有指向前一个节点的指针)。
- 节点在内存中可以不连续存放。
二、访问方式
-
数组
- 可以通过索引直接访问任意位置的元素,时间复杂度为 O(1)。
- 例如,要访问数组中的第 5 个元素,可直接根据索引计算出该元素在内存中的地址并进行访问。
-
链表
- 要访问特定位置的元素,需要从链表的头节点开始,依次遍历每个节点,直到找到目标位置的节点,时间复杂度为 O(n),其中 n 是链表的长度。
三、插入和删除操作
-
数组
- 在数组中间插入或删除元素时,需要移动大量后续元素以保持数组的连续性,时间复杂度通常为 O(n)。
- 例如,在一个有 n 个元素的数组中间插入一个元素,需要将插入位置后的 n - 插入位置个元素向后移动一位。
-
链表
- 在链表中间插入或删除元素相对较容易,只需修改相关节点的指针即可,时间复杂度为 O(1)。
- 例如,在一个链表中间插入一个节点,只需将新节点的指针指向插入位置后的节点,插入位置前的节点的指针指向新节点。
四、空间占用
-
数组
- 数组的大小在创建时就确定,可能会存在空间浪费的情况。如果数组的大小设置得过大,而实际存储的元素较少,就会浪费内存空间;如果数组的大小设置得过小,可能无法满足存储需求。
- 但是,由于数组是连续存储,CPU 缓存利用率相对较高。
-
链表
- 链表的每个节点除了存储数据外,还需要额外的空间存储指针,因此会有一定的空间开销。
- 链表的大小可以动态调整,不会出现空间浪费的情况,但在频繁的插入和删除操作中,可能会导致内存碎片的产生。
五、应用场景
-
数组
- 适用于需要频繁随机访问元素的场景,如数值计算、矩阵运算等。
- 当已知数据规模且对内存空间的利用率要求较高时,也可以使用数组。
-
链表
- 适用于频繁插入和删除元素的场景,如操作系统的内存管理、链表实现的栈和队列等。
- 当数据规模不确定或者需要动态调整大小的情况,链表是一个较好的选择。
基于数组和基于链表实现数据结构
以下分别介绍基于数组和基于链表实现数据结构的方式。
一、基于数组实现数据结构
以实现栈为例:
-
定义栈结构:
- 首先确定数组的大小,创建一个固定大小的数组来存储栈中的元素。
- 同时,维护一个变量来记录栈顶的位置,初始值为 -1,表示栈为空。
-
入栈操作(push):
- 检查栈是否已满。如果栈顶位置等于数组大小减 1,则栈已满,不能进行入栈操作。
- 如果栈未满,将栈顶位置加 1,然后将元素放入数组中对应栈顶位置的位置。
-
出栈操作(pop):
- 检查栈是否为空。如果栈顶位置为 -1,则栈为空,不能进行出栈操作。
- 如果栈不为空,取出数组中栈顶位置的元素,然后将栈顶位置减 1。
-
获取栈顶元素(peek):
- 检查栈是否为空。如果栈为空,返回 null 或特定的错误值。
- 如果栈不为空,直接返回数组中栈顶位置的元素,而不改变栈顶位置。
二、基于链表实现数据结构
同样以实现栈为例:
-
定义栈结构:
- 定义链表节点类,包含数据和指向下一个节点的指针。
- 创建一个栈类,包含一个指向栈顶节点的指针,初始值为 null,表示栈为空。
-
入栈操作(push):
- 创建一个新节点,将新节点的数据设置为要入栈的元素。
- 将新节点的下一个指针指向当前栈顶节点。
- 更新栈顶指针为新节点。
-
出栈操作(pop):
- 检查栈是否为空。如果栈为空,不能进行出栈操作。
- 如果栈不为空,取出栈顶节点的数据,然后将栈顶指针指向当前栈顶节点的下一个节点,释放原栈顶节点的内存。
-
获取栈顶元素(peek):
- 检查栈是否为空。如果栈为空,返回 null 或特定的错误值。
- 如果栈不为空,返回栈顶节点的数据,而不改变栈的结构。
基于数组实现数据结构的优点是可以随机访问元素,访问速度快,但插入和删除元素可能需要移动大量元素,效率较低。基于链表实现数据结构的优点是插入和删除元素非常高效,只需修改指针即可,但随机访问元素需要遍历链表,效率较低。在实际应用中,可以根据具体需求选择合适的数据结构实现方式。
无序表和有序表
无序表和有序表是两种不同的数据结构类型,它们在数据存储和操作方面有以下区别:
一、数据存储方式
-
无序表
- 数据元素在表中没有特定的顺序。
- 可以使用数组或链表等数据结构来实现。例如,用链表实现的无序表,各个节点可以在内存中的任意位置,节点之间的连接关系并不反映数据元素的大小顺序。
-
有序表
- 数据元素按照特定的顺序排列,通常是升序或降序。
- 常见的实现方式有数组和链表。以数组实现的有序表,元素在内存中连续存储,并且按照顺序排列;用链表实现的有序表,节点按照数据元素的顺序依次连接。
二、查找操作
-
无序表
- 进行查找时,需要逐个遍历表中的元素,直到找到目标元素或遍历完整个表。
- 时间复杂度通常为 O(n),其中 n 是表中元素的个数。例如,在一个无序的链表中查找特定值的节点,需要从链表的头节点开始,依次检查每个节点的数据是否等于目标值。
-
有序表
- 可以利用数据的有序性进行更高效的查找。
- 对于使用数组实现的有序表,可以使用二分查找等算法,时间复杂度为 O(log n)。在链表实现的有序表中,可以根据数据的顺序进行有方向的遍历查找,效率通常也比无序表的遍历查找高。
三、插入操作
-
无序表
- 插入元素时,只需要将新元素添加到合适的位置(如链表的末尾或数组的空闲位置)即可,无需考虑元素的顺序。
- 时间复杂度取决于实现方式,对于链表实现,插入操作通常为 O(1),因为只需修改指针;对于数组实现,如果不考虑可能的数组扩容操作,插入到末尾的时间复杂度为 O(1),插入到中间位置需要移动后续元素,时间复杂度为 O(n)。
-
有序表
- 插入新元素时,需要先找到合适的位置以保持数据的有序性。
- 对于数组实现,可能需要移动大量元素来为新元素腾出合适的位置,时间复杂度通常为 O(n)。对于链表实现,需要遍历链表找到合适的插入位置,时间复杂度为 O(n)。
四、应用场景
-
无序表
- 适用于对数据顺序不敏感的场景,或者数据的插入和删除操作频繁且不要求保持特定顺序的情况。例如,存储一组随机生成的数字,或者实现一个简单的集合数据结构。
-
有序表
- 适用于需要快速查找特定范围数据的场景,或者需要按照特定顺序处理数据的情况。例如,实现一个按时间顺序排列的日志系统,或者进行数值范围查询的数据库索引。
树
树是一种非线性的数据结构,具有以下特点和重要概念:
一、基本结构
树由节点和边组成。
- 节点:包含数据和指向其他节点的指针(在某些树的实现中,节点还可以包含其他信息,如父节点指针、节点颜色等)。
- 边:连接节点,代表节点之间的关系。
二、重要概念
- 根节点:树中唯一没有父节点的节点,它是树的起点。
- 子节点和父节点:一个节点的直接后继节点称为该节点的子节点,而该节点则是其子节点的父节点。
- 叶节点:没有子节点的节点。
- 节点的度:一个节点拥有的子树的个数。
- 树的度:树中所有节点的度的最大值。
- 树的深度(高度):从根节点到叶节点的最长路径长度。
三、常见类型的树
- 二叉树:每个节点最多有两个子节点(左子节点和右子节点)。
- 满二叉树:所有叶节点都在同一层,并且每个非叶节点都有两个子节点。
- 完全二叉树:除了最后一层,其他层的节点都是满的,并且最后一层的节点从左到右依次排列。
- 平衡二叉树:左右子树的高度差不超过 1 的二叉树,常见的平衡二叉树有 AVL 树、红黑树等。平衡二叉树可以保证在插入和删除节点时,树的高度不会增长过快,从而保持较高的查找效率。
- 二叉搜索树:对于二叉搜索树中的任意一个节点,其左子树中的所有节点的值都小于该节点的值,右子树中的所有节点的值都大于该节点的值。这使得二叉搜索树在查找、插入和删除操作上具有较高的效率,时间复杂度为 O(log n),其中 n 是树中节点的个数。
四、应用场景
- 文件系统:文件系统中的目录结构可以用树来表示,根节点代表文件系统的根目录,每个子节点代表一个子目录或文件。
- 数据库索引:数据库中的 B 树和 B+树等数据结构都是基于树的变体,用于快速查找和存储数据。
- 决策树:在机器学习和数据挖掘中,决策树用于分类和预测问题。决策树通过对数据的特征进行逐步划分,形成一个类似于树的结构,每个内部节点代表一个特征的判断,叶节点代表最终的分类结果。
- 语法树:在编译原理中,语法树用于表示程序的语法结构。语法树的每个节点代表一个语法单元,如表达式、语句、函数等,通过对程序代码进行分析和构建语法树,可以进行语法检查、代码优化等操作。
图
图是一种复杂的数据结构,由顶点和边组成,用于表示事物之间的关系。以下是关于图的详细介绍:
一、基本组成
- 顶点(Vertex):也称为节点,代表图中的对象或实体。每个顶点可以有自己的属性,如名称、标签、权重等。
- 边(Edge):连接两个顶点的线段,表示顶点之间的关系。边也可以有属性,如权重、方向等。
二、图的分类
- 无向图:边没有方向,即如果顶点 A 和顶点 B 之间有一条边,那么可以从 A 到达 B,也可以从 B 到达 A。
- 有向图:边有方向,即如果有一条从顶点 A 指向顶点 B 的边,那么只能从 A 到达 B,不能从 B 到达 A。
- 带权图:边具有权重,表示顶点之间关系的强度或代价。例如,在交通网络中,边的权重可以表示两个城市之间的距离或交通费用。
三、图的表示方法
- 邻接矩阵(Adjacency Matrix):用一个二维矩阵来表示图。矩阵的行和列分别代表图中的顶点,如果顶点 i 和顶点 j 之间有边相连,则矩阵中第 i 行第 j 列的元素为 1(或边的权重),否则为 0。邻接矩阵适用于顶点数量较少且边比较密集的图,但对于稀疏图会浪费大量的存储空间。
- 邻接表(Adjacency List):为每个顶点建立一个链表,链表中存储与该顶点相邻的顶点。邻接表适用于顶点数量较多且边比较稀疏的图,可以节省存储空间。
四、图的遍历
- 深度优先搜索(Depth-First Search,DFS):从图中的一个顶点开始,沿着一条路径尽可能深地探索,直到无法继续前进,然后回溯到上一个顶点,继续探索其他未访问的路径。深度优先搜索可以用递归或栈来实现。
- 广度优先搜索(Breadth-First Search,BFS):从图中的一个顶点开始,先访问该顶点的所有相邻顶点,然后再依次访问这些相邻顶点的相邻顶点,直到访问完所有顶点。广度优先搜索可以用队列来实现。
五、应用场景
- 社交网络分析:图可以表示社交网络中的用户和他们之间的关系,如朋友关系、关注关系等。通过分析图的结构,可以发现社交网络中的社区、关键人物、信息传播路径等。
- 交通网络规划:图可以表示城市之间的道路网络或公共交通线路。通过图的算法,可以计算最短路径、最优路线、交通流量等,为交通规划和导航提供支持。
- 电路设计:在电子电路设计中,图可以表示电路中的元件和它们之间的连接关系。通过分析图的结构,可以进行电路的故障诊断、优化设计等。
- 生物信息学:在生物信息学中,图可以表示蛋白质之间的相互作用、基因调控网络等。通过分析图的结构,可以揭示生物系统的功能和机制。
子程序与参数
子程序是一个相对独立的程序模块,通常用于执行特定的任务或操作。参数则是在调用子程序时传递给它的值,用于影响子程序的行为和结果。
一、子程序的特点和作用
- 模块化:将复杂的程序分解为多个子程序,每个子程序负责一个特定的功能,使得程序结构更加清晰,易于维护和修改。
- 可重用性:一旦编写了一个子程序,可以在多个不同的地方调用它,避免了重复编写相同的代码,提高了开发效率。
- 抽象性:子程序隐藏了内部的实现细节,只对外提供一个接口,使得调用者不需要了解子程序的具体实现,只需要知道如何调用它以及它的功能是什么。
二、参数的类型和作用
- 形式参数(形参):在子程序定义中出现的参数,用于接收调用者传递的值。形参只是一个占位符,在子程序内部代表一个变量,其具体的值在调用时确定。
- 实际参数(实参):在调用子程序时传递给形参的值。实参可以是常量、变量、表达式等。
- 参数的作用:参数可以影响子程序的行为和结果。通过传递不同的参数,子程序可以执行不同的操作或计算不同的结果。例如,一个计算圆面积的子程序可以接收一个半径作为参数,通过不同的半径值可以计算出不同大小的圆的面积。
三、参数传递的方式
- 值传递:将实参的值复制一份传递给形参。在子程序内部对形参的修改不会影响到实参的值。
- 引用传递:将实参的地址传递给形参。在子程序内部对形参的修改会影响到实参的值。
- 指针传递:与引用传递类似,将实参的地址传递给形参,但使用指针来表示。在子程序内部可以通过指针间接访问实参的值,并进行修改。
四、应用场景
- 数学计算:例如,计算两个数的和、差、积、商等,可以编写一个子程序,接收两个数作为参数,返回计算结果。
- 文件操作:例如,打开文件、读取文件内容、写入文件等,可以编写一个子程序,接收文件名作为参数,执行相应的操作。
- 图形绘制:例如,绘制不同形状的图形,可以编写一个子程序,接收图形的参数(如半径、边长、颜色等),绘制出相应的图形。
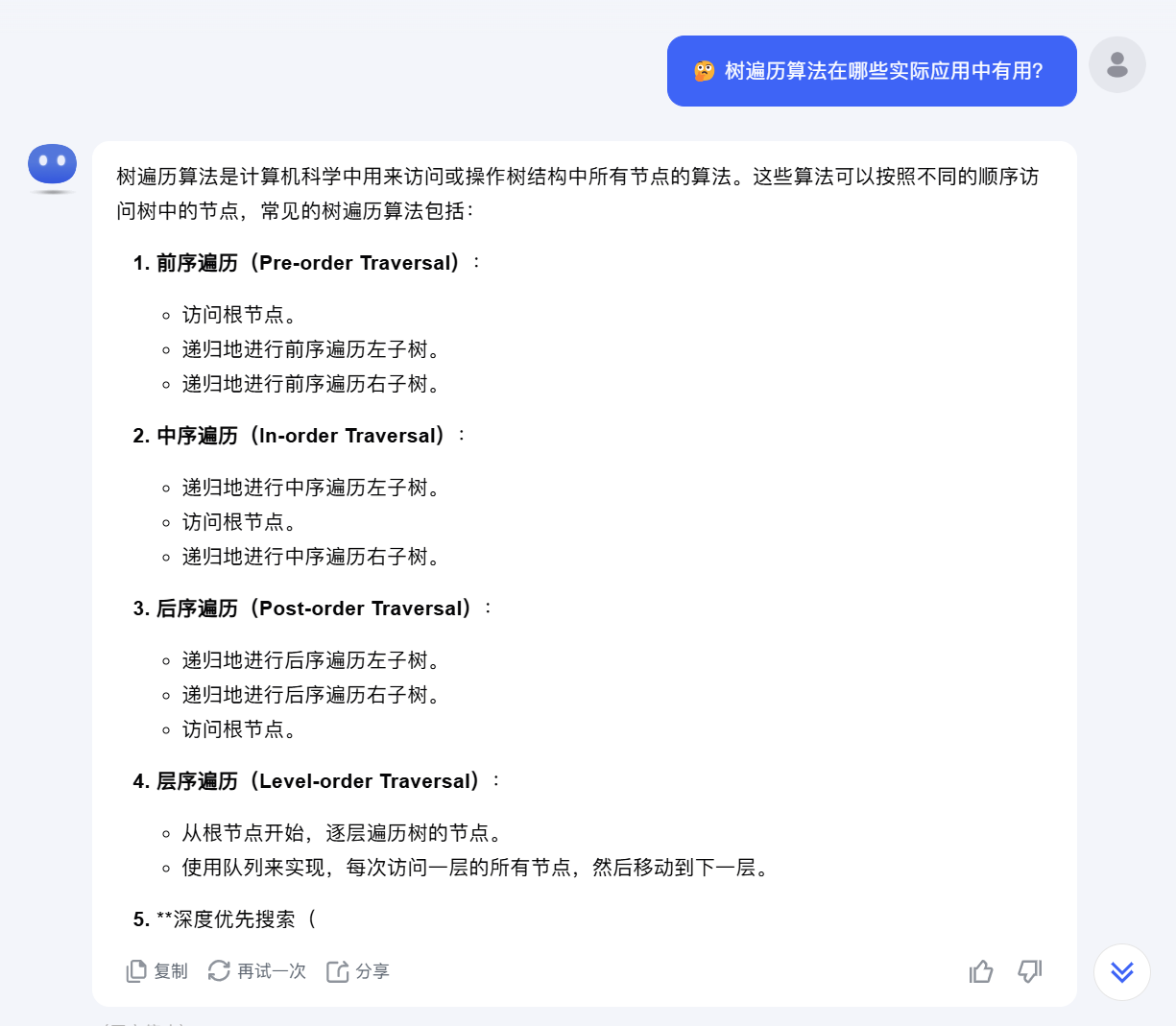
基于AI的学习

学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 500/1000 | 3/7 | 22/60 | |
| 第四周 | 300/1300 | 2/9 | 30/90 | |
| 第五周 | 200/200 | 2/2 | 20/20 | |
| 第六周 | 300/500 | 2/4 | 18/38 | |
| 第七周 | 500/1000 | 3/7 | 22/60 |