E. Building an Aquarium
题目
有一块由 \(n\) 根柱子组成的珊瑚,其中 \(i\) 根柱子高 \(a_i\) 个单位。之后,在珊瑚周围建造一个水族箱,具体如下:
- 选择一个整数 \(h \geq 1\) --水箱的高度。在水箱两侧建造高度为 \(h\) 的墙壁。
- 然后,在水箱中注满水,使每一列的高度都是 \(h\) ,除非珊瑚的高度超过 \(h\) ,否则这一列不需要注水。
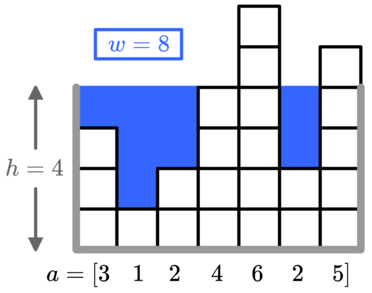
例如, \(a=[3,1,2,4,6,2,5]\) 和高度为 \(h=4\) ,最终总共需要使用 \(w=8\) 个单位的水,如图所示。
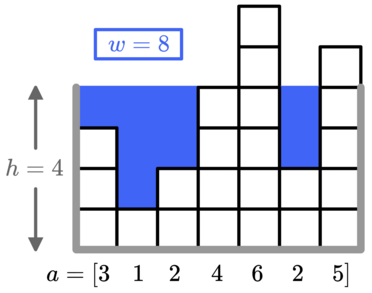
最多可以用 \(x\) 个单位的水来装满水箱,尽可能建造最大的水箱。可以选择的 \(h\) 的最大值是多少?
INPUT
第一行包含一个整数 \(t\) ( \(1 \leq t \leq 10^4\) ) - 测试用例数。
每个测试用例的第一行包含两个正整数 \(n\) 和 \(x\) ( \(1 \leq n \leq 2 \cdot 10^5\) ; \(1 \leq x \leq 10^9\) )--珊瑚的列数和最大水量。
每个测试用例的第二行包含 \(n\) 个空格分隔的整数 \(a_i\) ( \(1 \leq a_i \leq 10^9\) ) - 珊瑚的高度。
所有测试用例中 \(n\) 的总和不超过 \(2 \cdot 10^5\) 。
OUTPUT
对于每个测试用例,输出一个正整数 \(h\) ( \(h \geq 1\) ) -水箱的最大高度,因此最多需要 \(x\) 个单位的水才能装满水箱
在这些限制条件下, \(h\) 这个值总是存在的
Example Input
5
7 9
3 1 2 4 6 2 5
3 10
1 1 1
4 1
1 4 3 4
6 1984
2 6 5 9 1 8
1 1000000000
1
Example Output
4
4
2
335
1000000001
Note
第一个测试案例如语句所示。在 \(h=4\) 的情况下,我们需要 \(8\) 个单位的水,但如果 \(h\) 增加到 \(5\) ,我们需要 \(13\) 个单位的水,这比 \(x=9\) 多。因此, \(h=4\) 是最佳方案。
在第二个测试案例中,我们可以选择 \(h=4\) ,并在每列中添加 \(3\) 个单位,总共使用 \(9\) 个单位的水。可以证明这是最佳方案。
在第三个测试案例中,我们可以选择 \(h=2\) ,并用掉所有的水,因此这是最优方案。
[!NOTE]
二分法伪代码:
[!TIP]
对数组a和整数x进行无限次操作,每次操作可以对数组a中任意一个数进行加法,加数的总和不超过x,求整个数组最小值的最大值
找到具有一定上限的最大高度→二元搜索
这个和砍树的思路是一样的,代码基本上可以照搬,但是要注意初始值
#include <bits/stdc++.h>using namespace std;int main()
{int t;scanf("%d", &t);for (int i = 1; i <= t; i++) {int n;long long x;scanf("%d %lld", &n, &x);long long a[n];for (int i = 0; i < n; i++) {scanf("%lld", &a[i]);}long long l = 0;long long r = 2000000000 + 10;while (l < r) {long long mid = l + r + 1 >> 1;//long long mid = l + (r - l + 1) / 2;long long sum = 0;for (int i = 0; i < n; i++)if (mid >= a[i]) {sum += mid - a[i];}if (sum <= x) {l = mid;} else {r = mid - 1;}}printf("%lld\n", l);}return 0;
}
[!TIP]
也可以用用sort排序再从后往前查找的方法,注意点同上(WA)
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;int main() {int t;cin >> t;for (int i = 1; i <= t; i++) {int n, x;cin >> n >> x;vector<long long> a(n + 1),s(n + 1);a[n] = 2e9+10;for (int j = 0; j < n; j++) {cin >> a[j];}// 对数组a进行排序sort(a.begin(), a.end());s[0] = a[0];for (int k = 1; k <= n; k++) {s[k] = s[k - 1] + a[k];}int fumo = 0; for (int l = 1; l <= n; l++){long long sum = (l + 1) * a[l] - s[l];if (sum > x) break;else fumo = l;}long long h = a[fumo];long long baka = x - ((fumo + 1) * a[fumo] - s[fumo]);h += baka / (fumo + 1);cout << h << '\n';}return 0;
}