0.0 前言
看了一个晚上,加上同桌的讲解,大致了解了二维数点问题的基本思路。
0.1 前置知识
-
可持久化线段树
-
树状数组
1.0 概述
二维数点问题的一般形式是形如“给定平面上 \(n\) 个点,每次询问给定一个矩形,求该位于矩形内的点的个数”一类问题,模板题为 P2163 [SHOI2007] 园丁的烦恼 在这里给出两种解法。
2.0 解法
2.0.1 引入
我们先从简化的一维问题开始:如果给定的都是一个数轴上的点,询问的都是某个区间内点的个数该怎么办?一个比较 trivial 的想法是将坐标离散化后扔进权值线段树内,询问的时候直接查询即可。
2.0.2 解法一:可持久化线段树
这里分享一种此题题解讲述较少的,不使用树状数组等其它数据结构的可持久化线段树的解法。
当问题扩展到二维之后,发现对于每一组纵坐标相同的点都建立一棵权值线段树似乎有些不太可行,可不可以用一棵线段树就维护所有点的信息呢?自然的,可持久化线段树就成为了首选,我们依旧先分别离散化横坐标和纵坐标,考虑先按其中一维(这里选择 \(x\) 这维)排序后一组一组地同时插入 \(x\) 相同的点至线段树中,并将另一维作为权值(这里选择 \(y\) 这维)。如果觉得还是很抽象的话可以看一个实例:
假设给定的是这些点(坐标已全部离散化,点的编号即为插入线段树的顺序):
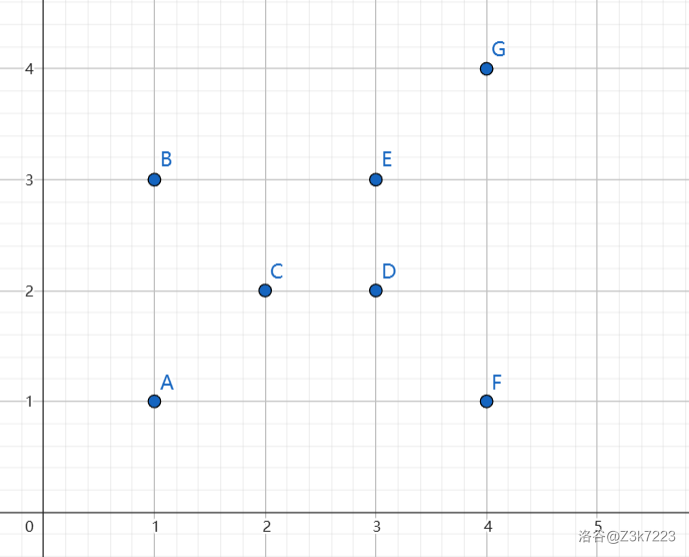
第一组,我们把 \(A,B\) 两点插入:
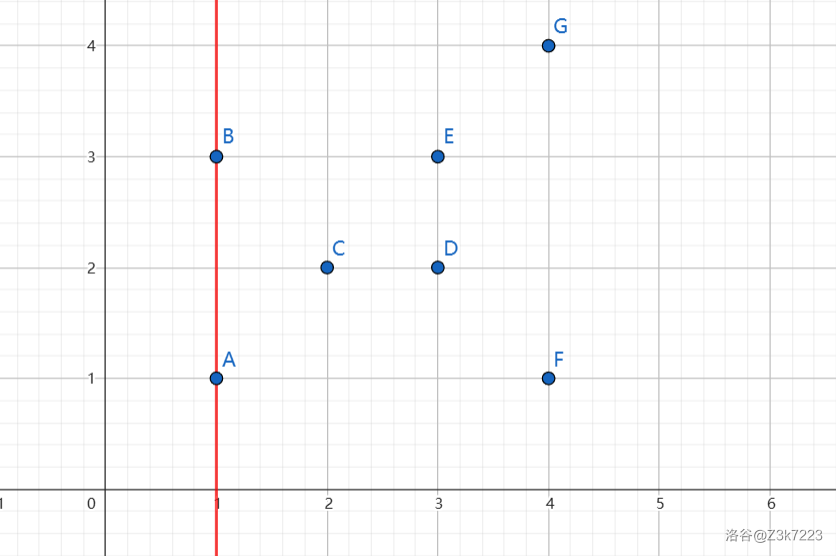
接着,继续向右走,插入 \(C\) 点:

依此类推,每次向右走,直到最后一个点被插入。
查询的时候,我们根据输入的坐标,找出离散化后对应的坐标。由于我们记下了整块插入时的根结点,因此我们只需要把这两个根节点的横坐标编号和对应的纵坐标扔进线段树查询即可。
解法一 Code
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, q;
int nx, ny;struct node {int x, y;
} a[N];
int tmpx[N], tmpy[N];
vector<int>t[N];
int rt[N];
int ls[N << 5], rs[N << 5], tree[N << 5];
int cnt;void build(int &p, int l, int r) {p = ++cnt;if (l == r) {return;}int mid = (l + r) >> 1;build(ls[p], l, mid);build(rs[p], mid + 1, r);
}int modify(int p, int l, int r, int k) {int x = ++cnt;ls[x] = ls[p], rs[x] = rs[p];tree[x] = tree[p] + 1;if (l == r) {return x;}int mid = (l + r) >> 1;if (k <= mid) {ls[x] = modify(ls[x], l, mid, k);} else {rs[x] = modify(rs[x], mid + 1, r, k);}return x;
}int query(int p1, int p2, int l, int r, int L, int R) {if (L <= l && r <= R) {return tree[p2] - tree[p1];}int mid = (l + r) >> 1;int res = 0;if (L <= mid) {res += query(ls[p1], ls[p2], l, mid, L, R);}if (R > mid) {res += query(rs[p1], rs[p2], mid + 1, r, L, R);}return res;
}int find_upx(int x) {int l = 1, r = nx, res = 0;while (l <= r) {int mid = (l + r) >> 1;if (x <= tmpx[mid]) {res = mid;r = mid - 1;} else {l = mid + 1;}}return res;
}int find_upy(int x) {int l = 1, r = ny, res = 0;while (l <= r) {int mid = (l + r) >> 1;if (x <= tmpy[mid]) {res = mid;r = mid - 1;} else {l = mid + 1;}}return res;
}int find_lowx(int x) {int l = 1, r = nx, res = 0;while (l <= r) {int mid = (l + r) >> 1;if (tmpx[mid] <= x) {res = mid;l = mid + 1;} else {r = mid - 1;}}return res;
}int find_lowy(int x) {int l = 1, r = ny, res = 0;while (l <= r) {int mid = (l + r) >> 1;if (tmpy[mid] <= x) {res = mid;l = mid + 1;} else {r = mid - 1;}}return res;
}int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> n >> q;if (!n) {while (q--) {cout << "0\n";}return 0;}for (int i = 1; i <= n; i++) {cin >> a[i].x >> a[i].y;tmpx[i] = a[i].x, tmpy[i] = a[i].y;}sort(tmpx + 1, tmpx + 1 + n), sort(tmpy + 1, tmpy + 1 + n);nx = unique(tmpx + 1, tmpx + 1 + n) - tmpx - 1;ny = unique(tmpy + 1, tmpy + 1 + n) - tmpy - 1;build(rt[0], 1, ny);for (int i = 1; i <= n; i++) {a[i].x = lower_bound(tmpx + 1, tmpx + 1 + nx, a[i].x) - tmpx;a[i].y = lower_bound(tmpy + 1, tmpy + 1 + ny, a[i].y) - tmpy;t[a[i].x].push_back(a[i].y);}for (int i = 1; i <= nx; i++) {rt[i] = rt[i - 1];for (auto j : t[i]) {rt[i] = modify(rt[i], 1, ny, j);}}while (q--) {int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;x1 = find_upx(x1), y1 = find_upy(y1);x2 = find_lowx(x2), y2 = find_lowy(y2);cout << query(rt[x1 - 1], rt[x2], 1, ny, y1, y2) << '\n';}return 0;
}