CF983-Div.2-E
自己独立完成的一道蓝题!中间思路有很多想复杂了的地方,但最终还是做出来了!记录一下自己的心路历程。
手玩样例找思路
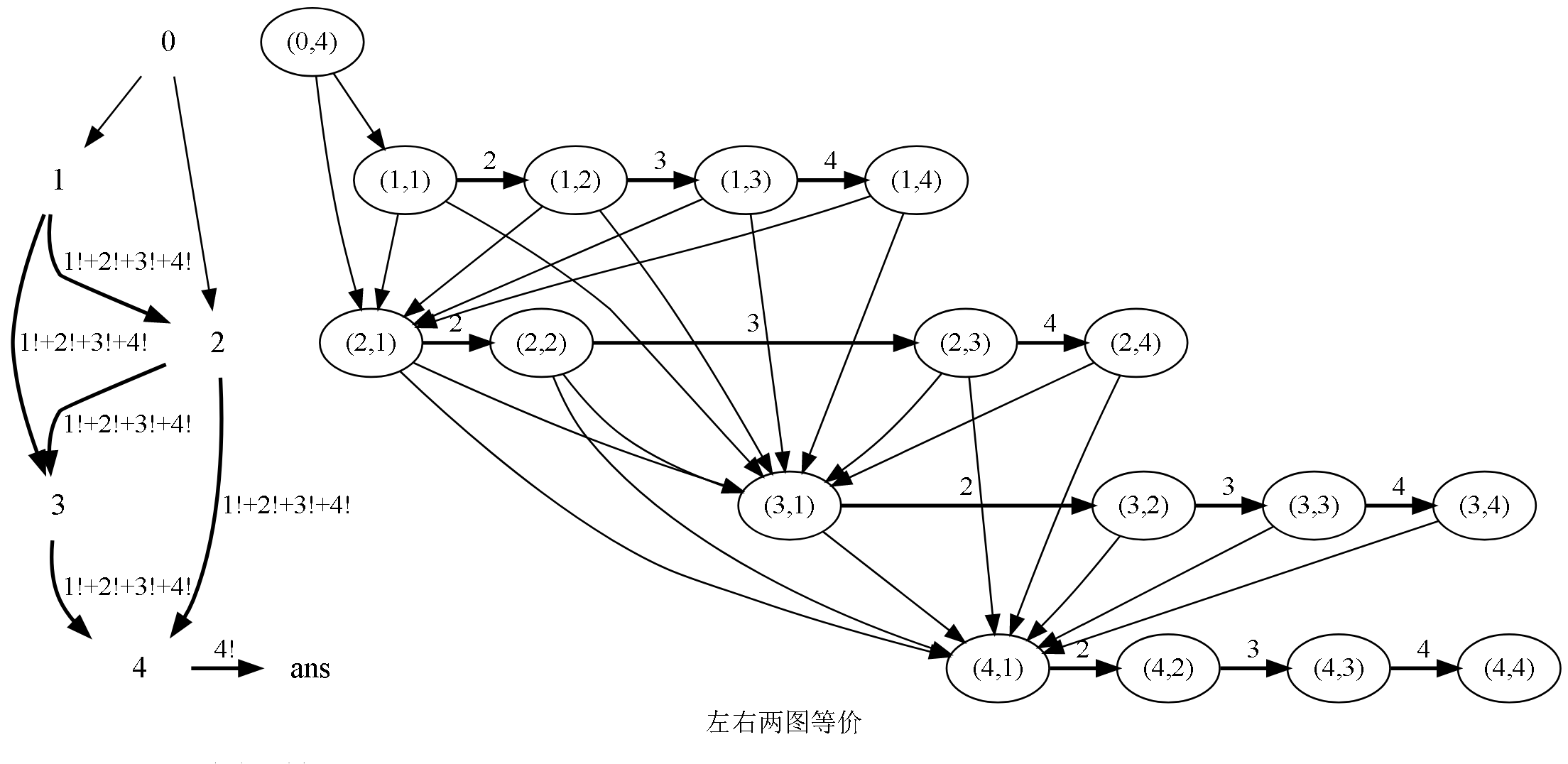
狂搓4个样例!搓到第4个,把每个位置操作完之后的序列都写下来观察,写的过程中猛然发现数和数之间的操作有一种一环扣一环的感觉,如果按顺序操作,上一个操作完了,到了当前这个,它的操作方式其实是很固定的。
想到解方程。又感觉本题很可以二分,因此想到二分 + 高斯消元的思路。时间复杂度 \(O(n^3logV)\)。
怎么快速解方程
不管能不能二分答案,先想固定每个数最终的值 \(x\) 过后,怎么判断这个方程有没有一组解,满足 \(v_{1 \sim n}\) 都是非负整数。
方程组写出来:
我们记 \(a_i = x - c_i\),\(c_i\) 表示原始序列(和原题不同)
完全满足3个3个轮换对称的形式,刚好 \(n\) 个方程,所以是有唯一解的。
考虑怎么避开高斯消元,比较快速地解出这个方程。
找找轮换对称有没有什么性质。首先全部加起来刚好是 4 倍的 \(\sum_{i = 1}^{n} vi\)。因此可以在 \(O(n)\) 时间内得到了 \(vsum\)。
接着想。想了一段时间发现对每个方程单独下手仍然不方便。就开始乱搞了,先是挑了几个方程出来看尽量能不能凑成接近一个 \(v_{1 \sim n}\) 的形式,发现没什么性质。
然后把所有的奇数项方程加了起来,发现得到:
进而在 \(O(n)\) 时间内得到了 \(v_1 + v_n\)。
依次带进原方程组中,记 \(b_i = a_i - (v_i + v_{i - 1})\),得到:
再次全部加在一起可以得 \(vsum\),但已经没用了。
再次把所有的奇数项方程加了起来,得到:
进而在 \(O(n)\) 时间内得到了 \(v_1\),最后就可以依次得到 \(v_1 \sim n\)
梳理思路
结合方程组理解每次操作,发现如果序列已经全部变成一样的数 \(x\) 了,此时每个位置在操作1次,相当于序列全部变成了 \(x + 4\),仍然是一组合法的解。结合题中所说的 “输出任意一个解”,更加肯定这个思路是对的。
于是发现不用二分了,对任意 \(x\),\(x - 2 \sim x + 2\) 中必然有一个值是可以生成一组合法解的。
\(x\) 取极大值就肯定有合法解了,我取的 1e18。
因此在 \(O(\sum n)\) 的时间内就可以解决这个问题。
#include<bits/stdc++.h>
#define F(i,l,r) for(int i(l);i<=(r);++i)
#define G(i,r,l) for(int i(r);i>=(l);--i)
using namespace std;
using ll = long long;
using super = __int128;
const int LEN = 5e6;
char buf[100], *p1 = buf, *p2 = buf, obuf[LEN], *o = obuf;
inline int gc(){return (p1 == p2) && (p2 = (p1 = buf) + fread(buf, 1, 100, stdin), p1 == p2) ? EOF : *p1++;
}
inline int rd(){int x = 0; char ch; bool f = 1;while(!isdigit(ch = gc())) f ^= (ch == '-');do x = (x << 3) + (x << 1) + (ch ^ 48); while(isdigit(ch = gc()));return f ? x : -x;
}
inline void output(super x){if(x < 0){x = ~x + 1;*o++='-';}if(x > 9) output(x / 10);*o++=(x % 10 + 48);
}
inline void write(super x, char c){output(x);*o++=c;
}
const int N = 2e5 + 5;
int n, T;
int c[N];
super v[N], a[N], b[N];
const int debug = 10004;
bool suan(ll x){super vsum = 0;b[0] = 0;F(i, 1, n) {a[i] = x - c[i];vsum += a[i];if(i & 1) b[0] += a[i];}if(vsum % 4 != 0) return 0;vsum /= 4;b[0] -= vsum * 2;v[1] = 0;F(i, 1, n){b[i] = a[i] - b[i - 1]; if(i & 1) v[1] += b[i];if(x == debug){cerr << (ll)b[i] << ' ';}}v[1] -= vsum;if(v[1] < 0) return 0;F(i, 2, n) {v[i] = b[i - 1] - v[i - 1];if(v[i] < 0) return 0;}return 1;
}
void Main(){n = rd();int flag = 1;F(i, 1, n) {c[i] = rd();if(i > 1 && c[i] != c[i - 1]) flag = 0;}if(flag){F(i, 1, n) write(0, ' ');return ;}const ll MAXN = 1e18;for(ll r = MAXN - 5; r <= MAXN; ++ r){if(suan(r)){F(i, 1, n) write(v[i], ' ');return ;}}
}
signed main(){
// freopen("E.in","r",stdin);
// freopen("E.out","w",stdout);T = rd();while(T --){Main();*o++='\n';}fwrite(obuf, o - obuf, 1, stdout);return fflush(0), 0;
}