涉及知识点:动态开点线段树,贪心
前言
很妙很感性直观的贪心,做完神清气爽。
题意
有一个长为 \(2^k\) 的序列,编号从 \(0\) 开始,你要在上面染色,每次只能染色 \([k2^i,(k+1)2^i-1]\) 的区间(\(0\leq i<k\)),问最少要染色多少次才能变成给定的目标序列。目标序列以形如 \((x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\) 的格式给出,表示从 \(0\) 开始有长为 \(x_1\) 的颜色为 \(y_1\) 的段,然后长为 \(x_2\) 颜色为 \(y_2\) 的段,以此类推。
\(k\leq 30,n\leq 10^5\)。
思路
不难发现合法的染色区间其实就是原序列建出的线段树上的某个节点,于是问题转化为了在线段树上选一些点染色,每个叶子节点的颜色为距离它最近的被染色节点的颜色。为什么是距离最近的?因为我们肯定是先染长的段再染短的段最优(否则,先染短的就可能被后染的长的覆盖),对应线段树上就是先染浅的节点再染深的节点。
于是我们对目标序列建出一颗线段树,但是本题的空间肯定不允许我们建完整的线段树,可以考虑动态开点,假设当前节点对应的区间都是同一种颜色,就可以停止继续往下建了。这样建树在 update 一次时最多涉及 \(\log_2(2^k)=k\) 个节点,因此时空复杂度均为 \(O(nk)\)。
注意:这样建出的线段树仍然满足普通线段树“要么没有儿子,要么有两个儿子”的性质,不存在只有左儿子或右儿子的情况。
接下来就在线段树上贪心,我们给每个节点开一个集合,意为“该节点所代表区间在最优策略下,如果被染色,那么可能染成的颜色”。首先叶子节点的集合肯定就只有它自己的颜色,\(ans=1\)。而对于非叶子节点,我们取它左右儿子的交集,如果这个交集不为空,我们就可以在这些颜色当中选一个作为当前区间的颜色,因此当前节点的集合为这个交集,且 \(ans\) 为 \(ans_{lch}+ans_{rch}-1\);如果交集为空,那么当前节点为左右儿子并集,且 \(ans\) 为 \(ans_{lch}+ans_{rch}\)。
这是什么意思呢?当左右孩子中有交集时,说明左右孩子都存在某个区间染的颜色相同,因此直接在当前节点染而不是在左右孩子分别染,可以节省一次操作,由于在此处染色会“阻断”更上方的染色,因此交集外的颜色不用再被考虑。如果没有交集,那么该节点染成什么也不会更优,打包取并集交给更上方的节点处理。
还有一个问题,所谓这样的“阻断”会使得贪心错误吗?实际上是不会的,假设某处本应该取交集但取了并集,导致祖先某处应该取并集却取了交集,相当于为了一个小段,去染色了一个本该是其他颜色的大段,这一定是不优的。
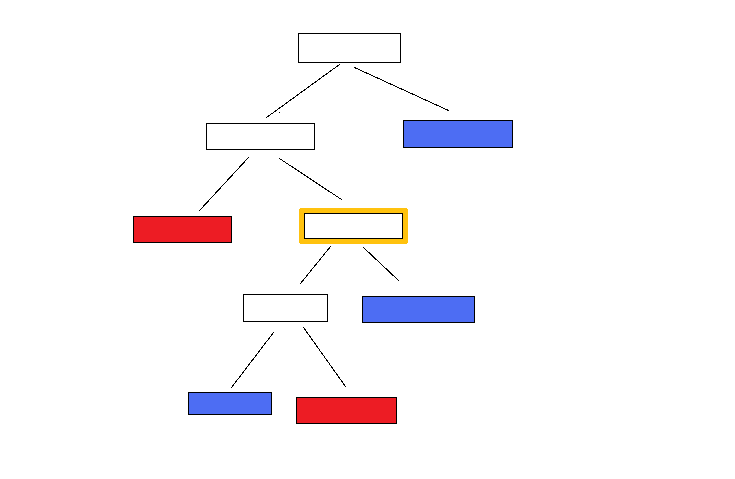
例:
可自行尝试将上图黄圈所示部分本来取交集为(蓝)改为取并集(红+蓝),答案变劣。
代码
这里讲一下 STL 的科技 set_intersection 和 set_union,当然还有个 set_difference,但此处没用到。
set_intersection(a.begin(),a.end(),b.end(),b.end(),inserter(c,c.begin())) 表示求 a 与 b 的交集存放到 c 中,其他两个同理。而且其时间复杂度为线性的,太伟大了 STL。
#define getmid int mid=(l+r)/2
int K,n,m,full;
struct Node{Node *lch,*rch;int t,ans;set<int>s;Node(){lch=rch=nullptr;t=-1;ans=0;}
};
Node* rt=nullptr;
void update(Node* &pos,int l,int r,int ll,int rr,int col){if(pos==nullptr) pos=new Node;if(ll<=l && r<=rr){pos->t=col;return;}getmid;if(ll<=mid) update(pos->lch,l,mid,ll,rr,col);if(mid<rr) update(pos->rch,mid+1,r,ll,rr,col);
}
void solve(Node* pos){if(pos->lch==nullptr){assert(pos->rch==nullptr);pos->s.insert(pos->t);pos->ans=1;return;}else{solve(pos->lch);solve(pos->rch);pos->ans=pos->lch->ans+pos->rch->ans;set_intersection(pos->lch->s.begin(),pos->lch->s.end(),pos->rch->s.begin(),pos->rch->s.end(),inserter(pos->s,pos->s.begin()));if(!pos->s.empty()){pos->ans--;return;}pos->s.clear();set_union(pos->lch->s.begin(),pos->lch->s.end(),pos->rch->s.begin(),pos->rch->s.end(),inserter(pos->s,pos->s.begin()));}
}
int main(){rd(K);rd(n);rd(m);full=(1<<K)-1;for(int i=1,x,y,l=0;i<=n;i++){rd(x);rd(y);update(rt,0,full,l,l+x-1,y);l+=x;}assert(rt);solve(rt);wt(rt->ans);return 0;
}