洛谷题单指南-二叉堆与树状数组-P3374 【模板】树状数组 1

原题链接：https://www.luogu.com.cn/problem/P3374

题意解读：树状数组模版：单点修改，区间求值。

解题思路：

树状数组-Binary Index Tree可以动态维护一组数，可以O(logn)的修改一个数，也可以O(logn)的计算一段区间的和。

思考一下朴素做法：如何修改一个数，计算区间和？

如果是常规数组，修改操作是O(1)，计算区间和需要先计算前缀和，复杂度为O(n)

如果是前缀和数组，修改操作是O(n)，计算区间和是O(1)

如果数据变更m次，总的复杂度将达到m*n

而树状数组可以使得两种操作的复杂度都是O(logn)。

1、树状数组定义

原数组：a[i]表示第i个数，

树状数组：tr[i]表示从i往前lowbit(i)个数的和，

lowbit(i)的含义是取整数i的最后一个二进制1所代表的整数，如i = 12，对应二进制1100，lowbit(i) = 4，

在c++中lowbit(i)的计算可以用i & -i。

2、利用树状数组求区间和

设s[x]为a[1]~a[x]的前缀和，根据tr[]的定义可知：

int sum(int x)

{

  for(int i = x; i > 0; i -= lowbit(i)) s[x] += tr[i];

}

i减lowbit(i)最多持续logn次，所以计算前缀和的复杂度为O(logn)

有了前缀和，l~r的区间和就很容易求得：s[r] - s[l-1]

3、利用树状数组修改元数组的值

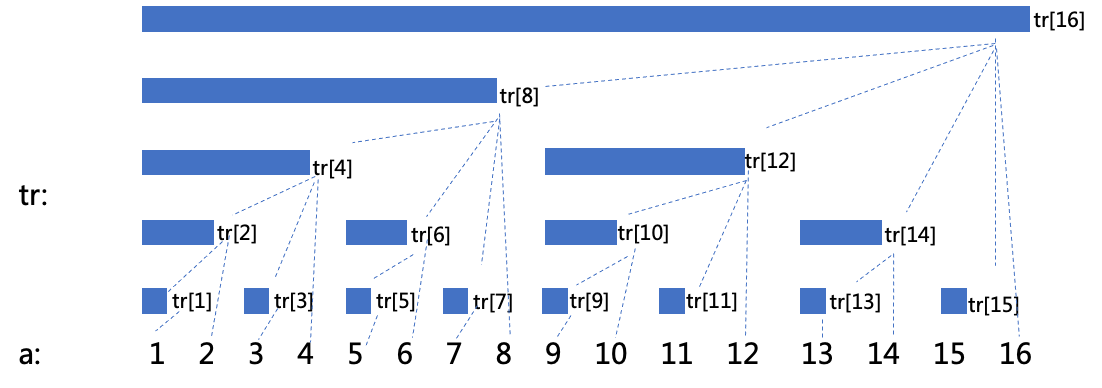
上图形式化表示a，tr的关系：

如tr[8]表示以a[8]往前lowbit(8)=8长度的a的元素之和，tr[12]表示以a[12]往前lowbit(12)=4长度的a的元素之和。

而

tr[16] = a[16] + tr[15] + tr[14] + tr[12] + tr[8]

tr[12] = a[12] + tr[11] 

tr[10] = a[10] + tr[9]

如此构成了一种树形关系，因此称为树状数组。

当要修改一个a元素的值a[x]，关键问题在于要同时跟新与a[x]有关的若干个tr值

比如修改了a[11]，显然在树中往根节点回溯即可找到所有受a[11]影响的tr值：tr[11]、tr[12]、tr[16]

11的二进制1011,12的二进制1100,16的二进制10000

它们的关系为：1011 + lowbit(1011) = 1100 ，1100 + lowbit(1100) = 10000

因此当修改一个a[x] += val，其所能影响的所有tr如下：

void add(int x, int val)

{

  for(int i = x; i <= n; i += lowbit(i)) tr[i] += val;

}

4、树状数组初始化

有两种初始化方法：

O(n * logn): 利用给元素增加值的函数，对于每一个a[i]，都add(i, a[i])

O(n): 先求a的前缀和s，对于tr[i] = s[i] - s[i - lowbit(i) + 1]

100分代码：

 

#include <bits/stdc++.h>
using namespace std;const int N = 500005;
int n, m;
int tr[N];int lowbit(int x)
{return x & -x;
}void add(int x, int val)
{for(int i = x; i <= n; i += lowbit(i)) tr[i] += val;
}int sum(int x)
{int res = 0;for(int i = x; i != 0; i -= lowbit(i)) res += tr[i];return res;
}int main()
{cin >> n >> m;int a;for(int i = 1; i <= n; i++) {cin >> a;add(i, a);}int op, x, y;while(m--){cin >> op >> x >> y;if(op == 1) add(x, y);else if(op == 2) cout << sum(y) - sum(x - 1) << endl;}return 0;
}