前面在文章《 访谈李继刚:从哲学层面与大模型对话 》中提到,继刚总结去年写提示词的核心理念是“清晰表达”,而今年则是“压缩表达”,既而才有火爆全网的Lisp风格提示词呈现给大家。
那么,为什么是压缩,或者说压缩表达的灵感来源是什么?从接下来的这篇文章中,我们可以对Lisp风格的提示词来源略窥一二。
这篇⽂章的作者是德国计算机科学家尤尔根·施密德胡⻉尔,他在⼈⼯智能领域有着深远的影响。施密德胡⻉尔教授不仅在强化学习、神经⽹络和⼈⼯智能历史⽅⾯是先驱,还成功创办了多家公司,包括专注于先进⼈⼯智能算法的Nnaisense。
因为施密德胡⻉尔教授的经历丰富,加上⽂章讨论的主题⽐较深,所以这篇⽂章可能读起来可能会有⼀些难度,建议⼤家先做好⼼理准备。
在⽂章中,施密德胡⻉尔提出了⼀个观点:当⼈或智能系统学会了新技能,能更有效地预测或压缩信息时,这些信息就会变得更吸引⼈。就像你学会了新技能,能更快解决难题,那难题⾃然就更有吸引⼒了。
他进⼀步解释说,新事物之所以让⼈兴奋,不是因为它们不寻常,⽽是因为它们让我们发现了新的、以前不知道的简单⽅法。这种愿望推动我们去探索未知,学习新知识,让我们的⼤脑或智能系统变得更聪明。
这种内在的动⼒激励着不同的⼈在各⾃的领域追求卓越:⽐如婴⼉探索世界,数学家解决难题,⾳乐家创作⾳乐,舞者跳舞,喜剧演员讲笑话,甚⾄是⿎励你⾃⼰去尝试新事物。
原文出处:《 Driven by Compression Progress: A Simple Principle Explains Essential Aspects of Subjective Beauty, Novelty, Surprise, Interestingness, Attention, Curiosity, Creativity, Art, Science, Music, Jokes 》
摘要
我认为,当⼀个有⾃我提升欲望但计算能⼒受限的观察者学会⽤更好的⽅法来预测或简化数据时,这些数据就会暂时显得有趣。这样的过程让数据在观察者看来变得更为简洁和美观。
好奇⼼,就是去追求创造或发现那些⾮随机、有规律的数据,这些数据之所以新奇和令⼈惊讶,并不是因为它们违背了常规,⽽是因为它们的规律性尚未被我们所了解,这使得我们能够进⼀步压缩和理解它们。
这种追求最⼤化了所谓的“有趣性”,也就是我们对美或可压缩性的主观感受,它相当于学习曲线的斜率。这种内在的驱动⼒激发了从探索中的婴⼉到数学家、作曲家、艺术家、舞者、喜剧演员、你⾃⼰,以及⾃1990年以来的⼈⼯智能系统去不断探索和学习。
1. 存储、压缩与奖励压缩进度
如果整个宇宙的历史都是可计算的[123, 124],⽽且⽬前没有证据反驳这种可能性[84],那么其最简洁的解释就是能计算出它的最短程序[65, 70]。遗憾的是,我们还没有⼀种通⽤的⽅法来找到计算任何给定数据的最短程序[34, 106, 107, 37]。因此,物理学家们传统上采取渐进的⽅法,每次只分析世界的⼀⼩部分,试图找到能够⽐先前已知的最佳定律更好地描述其有限观测结果的简单规律。本质上,这是在寻找⼀个能⽐已知最佳程序更有效地压缩观测数据的程序。
举例来说,⽜顿的万有引⼒定律可以表述为⼀⼩段代码,这使得许多涉及苹果和其他物体下落的观测序列得以⼤幅压缩。尽管其预测能⼒有限——例如,它⽆法解释苹果原⼦的量⼦波动——但在假定该定律成⽴的条件下,它仍然可以通过为那些⾼概率可预测的事件分配短代码,从⽽⼤⼤减少编码数据流所需的⽐特数[28]。
爱因斯坦的⼴义相对论理论带来了额外的压缩进展,因为它简洁地解释了许多之前⽆法⽤⽜顿理论预测的偏差现象。
⼤多数物理学家都认为,我们在物理学领域还有进步的空间。不过,想让⾃⼰的观察结果更客观、更精炼的,不只是物理学家。
简单说,那些能从过去找到规律、预测未来的⼈,他们都会想办法让⾃⼰对事情的理解和判断更简洁、更⾼效。
很久以前,⽪亚杰就通过他的“同化”和“适应”概念,解释了孩⼦们的探索性学习⾏为。
同化,就是把新知识融⼊到旧知识中,这有点像信息压缩。适应,就是调整旧知识来适应新知识,这有点像压缩技术的改进。
但⽪亚杰的想法太随意,没有提供⾜够的细节,所以计算机⽆法模拟他的想法。 那么,我们怎么在⼈造系统⾥模拟这种压缩技术的进步呢?
想象⼀下,⼀个智能体正在和它⼀开始不了解的世界互动。我们可以⽤我们的“强化学习(Reinforcement Learning)”框架,让这个智能体发现那些能带来额外压缩进步和提⾼预测能⼒的数据。
【译者注:强化学习是⼀种机器学习⽅法,它通过奖励和惩罚来训练算法,使其能够学习在特定环境中采取哪些⾏动以最⼤化某种累积奖励。简单来说,就是让计算机程序通过不断尝试和犯错,学会在给定情况下做出最佳选择。】
这个框架通过⿎励智能体主动探索,帮助它更好地理解世界,哪怕外界的奖励很少或者根本没有。智能体通过内在的奖励(即好奇⼼奖励)被激励去探索,从⽽发现输⼊数据流中与动作相关的、之前未知的规律。
1.1 概述
在 1.2 节我们将简要介绍我们的算法框架,它基于三个核⼼要素:
- ⼀个能够不断从数据历史中学习并改进的预测器或压缩器。
- ⼀个可计算的度量,⽤来衡量压缩器的进展,这将作为内在奖励的依据。
- ⼀个奖励优化器或强化学习器,它将奖励转化为⾏动,以期在未来获得更多的奖励。
具体的技术细节和理论概念将在附录中详细阐述,包括离散时间的实现⽅式。
在 1.3 节我们将探讨框架与外部奖励的关系,这⾥的“外部”指的是那些源⾃⼤脑之外,控制其“外部”⾝体⾏为的奖励。
第 2 节将⾮正式地展⽰,智能和认知的许多基本要素,如新奇性、惊喜性、趣味性的检测,⽆监督的注意⼒转移,主观美感,好奇⼼,创造⼒,艺术,科学,⾳乐和笑话,都可以看作是我们框架的⾃然结果。
特别是,我们将摒弃传统的玻尔兹曼/⾹农惊喜概念,并证明科学和艺术都可以被视为⼀种渴望,即通过创造或发现新的⽅式来压缩更多的数据。
第 3 节将概述这个框架的近似实现,这些实现已经在过去的⼯作中得到了应⽤。
第 4 节将把理论应⽤于为⼈类观察者量⾝定制的图像,展⽰从较低到较⾼主观可压缩性的奖励学习过程。
第 5 节将概述如何改进我们先前的实现,以及如何在⼼理学和神经科学中进⼀步检验我们的理论预测。
1.2 算法架构
这组简单的算法原则,其实质是将之前关于这个主题的出版物中的⼀些核⼼观点进⾏了提炼和总结[57、58、61、59、60、108、68、72、76、81、88、87、89]。正如我们之前提到的,具体的技术细节都放在了附录⾥了。在第 2 节中,我们讨论了这些原则,它们⾄少在定性上能够解释智能主体(⽐如⼈类)的很多⽅⾯。这启发了我们,让我们想要在认知机器⼈和其他⼈⼯系统中去实现和测试这些原则。
-
存储⼀切。 在与世界互动的过程中,要保存所有⾏为和感官观察的完整原始记录,包括奖励信号。数据是宝贵的,因为它是我们了解世界的唯⼀基础。想象⼀下,存储完整的数据并⾮不可能:⼀个⼈的⽣命很少能超过 10 亿秒。⼈脑⼤约有 860 亿个神经元,每个神经元平均有 7000 个突触。假设⼤脑⼀半的容量⽤于存储原始数据,并且每个突触最多可以存储 6 位信息,我们仍然有⾜够的空间以⼤约 100 兆⽐特/秒的速度记录⼀⽣的感官输⼊,这与⼀部⾼清电影的需求相当。⽽现代技术系统的存储能⼒很快就会超过这个⽔平。记住,如果能够存储数据,就不要轻易丢弃它!
-
增强数据的可压缩性。 理论上,数据中存在的任何规律性都可以被⽤来进⾏压缩。压缩后的数据,可以看作是对原始数据的⼀种简化解释。因此,为了更有效地解释世界,我们可以将⼀部分计算资源投⼊到⾃适应压缩算法的开发中,以尝试对数据进⾏部分压缩。例如,⾃适应神经⽹络可能能够学习如何从其他历史数据中预测或推断出某些数据,从⽽逐步减少对整体数据编码所需的⽐特数。请参⻅附录 A.3 和 A.5 。
-
让内在好奇⼼奖励反映数据压缩的进展。 智能体需要监控⾃适应数据压缩器的优化情况:每当它学会⽤更少的⽐特数来编码历史数据时,就根据学习或压缩的进展(也就是节省的⽐特数)来产⽣相应的内在奖励或好奇⼼奖励。参⻅附录 A.5 和 A.6 。
-
最⼤化内在好奇⼼奖励 [57, 58, 61, 59, 60, 108, 68, 72, 76, 81, 88, 87]。让⾏动选择器或控制器运⽤通⽤的强化学习(RL)算法,这个算法需要能够观察⾃适应压缩器的当前状态,以最⼤化期望奖励,特别是内在好奇⼼奖励。为了优化内在好奇⼼奖励,⼀个好的 强化学习算法会引导智能体的注意⼒和学习焦点,集中在那些能够发现或创造新的、未知但可学习的规律性的世界⽅⾯。简单来说,它将努⼒让压缩器的学习曲线变得更陡峭。这种主动的⽆监督学习有助于我们更好地理解世界是如何运作的。详⻅附录 A.7, A.8, A.9, A.10。
这个框架本质上是给好奇或有创造⼒的系统定了个⽬标,⽽不是说⼀定要⽤特定的压缩器、预测器或者强化学习算法来达到这个⽬标。我们后⾯会聊聊,有哪些可能的选择,能让这个框架变成具体的实例,包括之前已经实现过的那些。
1.3 与外部奖励的关系
当然,很多智能体的⽬标不仅仅是为了满⾜⾃⼰的好奇⼼,更重要的是解决实际问题。任何可以明确表述的问题,都能转化为⼀个强化学习问题:⼀个智能体在⼀个可能未知的环境中,努⼒在有限的⽣命周期内,最⼤化其预期的未来奖励。
进⼊新世纪,我们看到了⼀种⾮常通⽤的强化学习算法,它们被称为通⽤问题解决器或通⽤⼈⼯智能(详⻅附录 A.8 和 A.9)。这些算法在理论上是完美的,但在实际应⽤中可能并不总是最佳选择,⽐如 [29, 79, 82, 83, 86, 85, 92]中提到的那些。
这些通⽤⽅法在学习进展、压缩进展以及好奇⼼的促进⽅⾯,能够⾃动发现并利⽤这些概念。那么,为什么我们还要费⼒去构建⼀个明确的、主动的好奇⼼实验框架呢?
答案之⼀是:当前的通⽤⽅法往往对⼀些与问题本质⽆关的恒定减速因素视⽽不⻅,将它们隐藏在理论计算机科学的渐近符号之下。
这导致了⼀个关键问题悬⽽未决:如果智能体在每个单位时间内只能执⾏⼀定量的计算指令(⽐如说,每秒能够进⾏10万亿次基础操作),那么我们该如何充分利⽤这些指令,尽可能地接近近期通⽤⼈⼯智能的理论极限,特别是在外部奖励稀缺的情况下,这在许多现实环境中是常态。
本⽂的核⼼观点是,在奖励稀缺的环境中,对于资源受限的强化学习⽽⾔,好奇⼼驱动是⼀个如此普遍且极为有⽤的概念,它应当被预设,⽽⾮从头学起,以节省计算时间——尽管这个节省可能是常数,但量可能依然巨⼤。
这种⽅法的内在假设是,在现实世界⾥,对过去更好的理解将有助于我们更准确地预测未来,并加速寻找解决外部任务的⽅案,同时忽略了⼀个可能性:好奇⼼有时可能适得其反,正如那句⽼话“好奇害死猫”。
2. 压缩进程驱动
让我们来聊聊智能和认知的这些基本要素,它们其实都是那些原则⾃然⽽然带来的结果。
2.1 紧凑的内部表征或符号:⾼效历史压缩的副产品
为了压缩迄今为⽌的观察历史,压缩器(例如预测神经⽹络)将⾃动为经常重复的事物创建内部表征或符号(例如,某些神经特征检测器的模式)。
哪怕预测能⼒有限,通过给那些⾼概率可预测的事件贴上简短的标签,我们依然能做到⾼效的信息压缩。
举个例⼦,太阳每天东升西落,这是再常⻅不过的现象。因此,⽤“⽇光”这样的内部符号来概括数据历史中的这种重复性,通过⼀⼩段可复⽤的内部代码来描述,⽐起单纯存储原始数据来说,要⾼效得多。
实际上,我们经常可以看到,预测性神经⽹络在训练数据上尽可能减⼩预测误差的同时,会作为副产品⽣成这样的内部(且具有层级性的)代码。
2.2 意识是压缩过程的独特副产品
在智能体的⼀举⼀动和感官接收中,有⼀样东西始终如影随形,那就是智能体本⾝。要想⾼效地记录下所有的数据历史,智能体需要创造⼀种内部的符号或代码,⽐如神经活动模式,来代表⾃⼰。⼀旦这种⾃我表征被激活,⽆论是通过新的感官输⼊还是其他⽅式,我们就可以称智能体为具有⾃我意识或意识。
这种直⽩的解释既没有丢掉我们对意识概念的直觉理解,⼜⽐其他近期的观点来得简洁明了。在本⽂的后续部分,我们不会给意识这个概念赋予任何神秘⾊彩——我们认为,它不过是智能体在持续解决问题和构建世界模型的过程中,通过数据压缩产⽣的⾃然副产品,⽽在本⽂的后续讨论中,意识也不会占据重要的位置。
2.3 懒惰⼤脑对美的主观感知,随时间⽽变化
想象⼀下,O(t)代表的是⼀位主观观察者O在特定时刻t的状态。“懒惰⼤脑”理论告诉我们,对于⼀个新的观察对象D,其主观上的美感B(D,O(t))(别提它有多吸引⼈了,那是另外⼀个话题——请翻到2.4节)实际上和编码D所需的信息量成正⽐。这⾥的信息量,是基于观察者凭借有限的先验知识,通过其⾃适应压缩器的当前状态来体现的。
举个例⼦,如果你要⾼效地编码之前⻅过的⼈脸,⼀个像神经⽹络这样的压缩器可能会觉得,⽣成⼀个“标准脸”的内在表⽰特别有⽤。当你要编码⼀张新⾯孔时,只需要记录它与“标准脸”的差别。所以,那些和“标准脸”差别不⼤的新⾯孔,主观上看起来会更美。同样地,对于那些具有⼏何规律,如对称性或简单⽐例的⾯孔,情况也是如此——理论上,压缩器可以利⽤任何规律来减少存储数据所需的信息量。
简单来说,如果⼏个⼦模式在某个观察者看来是可⽐较的,那么主观上最美的那个,就是⽤观察者当前特定的编码和记忆⽅法,描述起来最简单(最短)的那个。⽐如,数学家们就喜欢那些⽤他们使⽤的形式语⾔简洁描述的简单证明。其他⼈则偏爱那些⼏何简单、美观、复杂度低的各类物体图画。
这就顺理成章地解释了,为什么许多⼈更偏爱和⾃⼰相似的⾯孔。他们每天照镜⼦看到的,会影响他们⼼中的“标准脸”,这背后其实是基于编码效率的考量。
2.4 主观趣味性:主观美的⼀阶导数,学习曲线的陡峭度
美丽的东西不⼀定吸引⼈。只有当它新奇,也就是说,当它那些简单的规律还没有被我们这些正在学习如何更有效地压缩信息的观察者完全理解时,它才显得有趣。我们可以将数据D对于观察者O在特定时间t的主观趣味性I(D,O(t))定义为:
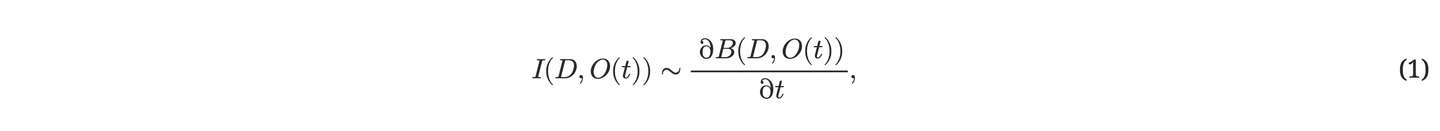
这便是主观美的⼀阶导数。随着学习者不断优化其信息压缩算法,原本看似杂乱⽆章的数据,逐渐在主观上变得有序和美丽,所需的编码⽐特也随之减少。只要这个过程还在进⾏,数据就依旧充满吸引⼒和价值。附录及第三章节中关于先前实现的讨论,将详细阐述这⼀概念的离散时间版本。同时,推荐阅读⽂献[59, 60, 108, 68, 72, 76, 81, 88, 87]以获取更深⼊的理解。
2.5 原始之美与趣味性 vs. 外部奖励
请注意,我们所讨论的关于美和趣味性的概念其实是有局限的,它们是纯粹的,因为这些概念并没有固有地与外部奖励带来的快乐联系在⼀起(详⻅第1.3节)。⽐如,有⼈会说,在寒冷的天⽓⾥泡个热⽔澡,会让⼈感到“美好”,这是因为满⾜了外部温度传感器预设的⽬标值,从⽽得到了⼀种奖励(这⾥的“外部”指的是⼤脑之外,即控制我们⾝体⾏为的⼤脑之外的部分)。⼜或者,某些⼈可能因为情感上的原因,⽐如与初吻时的美好回忆联系在⼀起,⽽称某⾸歌为“美妙”。但这并不是我们在这⾥讨论的重点——我们关注的是那些基于学习进步的内在型奖励。
2.6 真正的新颖性和惊喜:与传统信息理论的对⽐
想象两个极端的例⼦,它们是那么⽆趣、平淡⽆奇、枯燥乏味:⼀个依赖视觉的智能体如果总是⾝处⿊暗,它所接收到的视觉信息就会变得极易压缩,不久之后,这些信息就会变得完全可预测,毫⽆变化。然⽽,如果它⾯对的是⼀个充满⽩噪声的屏幕,尽管按照传统观点,这种屏幕充满了信息量和所谓的“新奇”与“惊喜”(这是根据玻尔兹曼和⾹农的定义[102]),但智能体所体验到的数据却是极其不可预测,且从本质上讲是不可压缩的。在这两种情况下,数据都是单调的[72, 88],因为它们都⽆法再进⾏进⼀步的压缩。因此,我们对传统意义上的“惊喜”进⾏了否定。⽆论是随机的还是完全可预测的数据,都不是真正新颖或令⼈惊讶的——只有那些还包含着未知算法规律的数据,才能称得上是新颖和令⼈惊喜的[57, 58, 61, 59, 60, 108, 68, 72, 76, 81, 88, 87, 89]。
2.7 专注⼒、好奇⼼与主动探索
当外部奖励不再出现,或者我们找不到提升预期外部奖励的新途径时,我们的“⼤脑”本质上是在追求新奇和趣味性的最⼤化。这就像主观美感或信息压缩性的⼀阶导数,也是我们学习曲线的陡峭度。 在受到信息压缩技术和改进算法的限制下,⼤脑会竭尽所能选择那些能够带来最⼤预期未来信息压缩进展的⾏动序列。
它会学会集中注意⼒和主动选择实验,专注于那些⽬前还难以压缩,但通过进⼀步学习有望变得可预测和可压缩的事项。对于已经能够主观理解并压缩的事物,它会逐渐失去兴趣。同样,对于那些⽬前看起来难以压缩,且根据现有经验似乎会⼀直保持这种状态的事物,或者那些要使其变得可压缩所要付出的成本远⾼于其他事物的事项,⼤脑同样会感到厌倦。
2.8 发现
异常巨⼤的压缩突破理应被称为发现。就像⽂章开头提到的,简单的万有引⼒定律,⽤⼀⼩段代码就能表达出来,但它却能极⼤地压缩我们之前对苹果下落和其他物体的所有观测结果。
2.9 突破传统的⽆监督学习
传统⽆监督学习的核⼼在于挖掘数据中的规律。 它通过数据聚类,或者利⽤具有统计独⽴性的因⼦编码[4, 64]来重新组织数据,甚⾄通过预测数据的⼀部分来推导出另⼀部分。这⼀切,本质上都是数据压缩的体现。⽐如,在数据点聚集的地⽅,我们可以通过其聚类中⼼和少量偏差信息来⾼效地编码这个数据点。当数据存在重复时,⼀个去冗余的因⼦编码[64]会⽐原始数据更加精简。⽽在数据具有可预测性的情况下,通过对那些⾼概率可从先前观察中预测的部分赋予短编码,同样可以实现压缩[28, 95]。总的来说,传统⽆监督学习的主要⽬标是通过发现⼀个能够快速计算并解释历史数据的程序,从⽽提⾼数据的压缩率,并且这个程序要⽐已知的最短程序更加简短。
但是,传统⽆监督学习还有所不⾜——它只能分析和编码数据,却⽆法对数据做出选择。我们需要在主动⾏为选择的维度上进⾏拓展,因为我们的⽆监督学习器不仅要分析数据,还要能够选择那些能够影响观察结果的⾏为。这就像是科学家挑选实验、婴⼉挑选玩具、艺术家选择⾊彩、舞者选择动作,或是任何专注系统[96]在选择下⼀个感官输⼊时的决策过程。⽽这,正是我们基于强化学习的好奇⼼和创造⼒框架所致⼒于实现的。
2.10 艺术与⾳乐:压缩进步的副产品
艺术和⾳乐,它们的价值远不⽌于社会层⾯。虽然有些⼈认为艺术是多余的,但优秀的艺术作品其实有着更深远的意义。那些令⼈钦佩的、与观察者紧密相连的艺术作品,能够拓宽我们对这个世界或可能世界的⻅解。
它们揭⽰了在可压缩数据中潜藏的、之前不为⼈知的规律,它们以⼀种令⼈惊喜的⽅式连接了原本孤⽴⽆援的模式,使得这些模式的组合在主观上变得更加易于压缩(艺术,作为启迪之眼),最终变得⼴为⼈知,失去新鲜感。
我提出⼀个假设:所有类型的艺术创作和专注的感知,其实不过是我们对新奇和好奇⼼的追求所带来的副产品,这种追求为压缩器的改进提供了源源不断的奖赏。
让我们深⼊探讨这个观点,延续 [81, 88] 中的讨论。⽆论是⼈⼯还是⼈类观察者,他们都需要按顺序感知艺术作品,并且通常是主动的。
⽐如,通过⼀系列视线转移或相机移动来观察⼀座雕塑,或者通过内部注意⼒的转移,过滤并突出钢琴家演奏的声⾳,同时忽略背景噪⾳。毫⽆疑问,许多⼈在欣赏艺术作品(如某些画作或歌曲)时,都能获得快乐和满⾜感。
但是,不同的观察者,他们拥有不同的感官装置和压缩算法,可能会偏好不同的输⼊序列。因此,任何关于“什么是好艺术”的客观理论,都必须将主观观察者作为变量来考虑。我们需要回答这样⼀个问题:观察者应该执⾏哪些动作序列,以及由此产⽣的注意⼒转移,才能最⼤化他们的快乐?
根据我们的原则,观察者应该选择那些能够最⼤化快速学习可压缩性的新序列。这意味着,他们应该选择那些与他们当前知识相匹配,并且能够适应他们(通常有限的)整合、学习或压缩新数据⽅式的序列。
2.11 ⾳乐
⽐如,⼀个⼈在选待播歌单的时候,应该挑哪⾸呢?肯定不是那⾸他已经连听了⼗次的,因为这⾸歌已经变得太容易预测了。但同样,也不是那种节奏和⾳调完全陌⽣的怪异新曲。这种曲⼦太不按常理出牌,充满了太多随意性和主观性。他应该试试那些既陌⽣⼜熟悉的歌曲,⾥⾯可能藏着⼀些出⼈意料的和声、旋律或节奏,但⼜⾜够让⼈迅速感受到声⾳流中的新规律或新压缩点。当然,这⾸歌迟早也会听腻,但⾄少现在还没到那个地步。
观察者依赖性可以通过⼀个现象来体现:与某些流⾏⾳乐相⽐,勋伯格的⼗⼆⾳体系⾳乐受欢迎程度要低得多。这可能是因为对于许多听众来说,⼗⼆⾳体系⾳乐的和声更为复杂,其算法结构不那么明显。⽐如,在⼗⼆⾳体系⾳乐中,连续⾳符的频率⽐通常不能简单地⽤⼩整数⽐来表⽰。但是,那些事先了解⼗⼆⾳体系⾳乐的基本概念、⽬标和限制的⼈,往往⽐那些没有这种背景的⼈更能够欣赏勋伯格的作品。
所有这些都和我们的原则相吻合:任何⼀个主观观察者的压缩器学习算法,都在尝试尽可能好地压缩他的声⾳和其他输⼊的历史。⾏动选择器则是在寻找那些能够影响历史,进⽽提升压缩器性能的⾏动。
那些有趣的⾳乐和其他序列,是因为它们包含了之前未知但可学习的新规律,从⽽推动了压缩器的进步。⽽那些⽆聊的模式,则是那些看起来随意或随机,或者结构太过复杂难以理解的模式。
2.12 绘画、雕塑、舞蹈、电影等艺术形式
这种说法不仅适⽤于电影和舞蹈这样的动态艺术,因为它们的动作可以压缩,也适⽤于绘画和雕塑。这是因为观众在欣赏这些艺术作品时,注意⼒的转移会产⽣⼀种动态的模式序列。
2.13 没有绝对的“理想⽐例”存在于预期与意外之间
在之前的研究中,⼀些学者试图从信息论的⻆度来解释美学体验。他们强调了美学对象传达的信息中,预期信息和⾮预期信息之间存在⼀个“理想”的⽐例(也就是它的“秩序”与“复杂性”之间的平衡)。但请注意,我们的⽅法并不需要假设这种客观存在的“理想”⽐例。 相反,我们提出了⼀种新的趣味性动态度量⽅法。这种⽅法关注的是编码⼀个对象所需的⽐特数的变化,并且会考虑到观察者的先验知识和他们使⽤的压缩算法的局限性。
2.14 艺术家的积极创作与观众的被动感知:界限模糊
正如观众在连续关注那些揭⽰出前所未知规律的艺术作品时获得内在的满⾜感⼀样,艺术家在创作这些作品时也能获得同样的奖励。
举个例⼦,我曾在经历了数百次令⼈失望的失败之后,终于发现那些简单的⼏何规律,它们让我得以绘制出图 1 和图 2 中的画作,这种发现让我感到⽆⽐的成就感。
然⽽,艺术家和观众之间的界限其实很模糊。他们都是在通过⼀系列⾏动来展现新的压缩形式。两者的内在驱动⼒都与我们的原则相契合。(译注:图 1 和图 2 在本⽂的后半部分)
当然,艺术家们在创作出真正新颖的艺术作品时,内⼼会得到⼀种基于创新的满⾜感。 同时,他们也希望得到外界的认可,⽆论是表扬还是⾦钱,或者两者都有。不过,我们的原则在理论上把这两种奖励形式区分开来。
2.15 艺术家和科学家之间的相似之处
在我们的视⻆下,科学家和艺术家其实颇为相似。他们都是通过精⼼挑选实验,去探索那些简单⽽⼜新颖的规律,以此来压缩他们的观察历程。
⽆论是画家、舞者、⾳乐家、纯数学家还是物理学家,他们的创造⼒都可以看作是我们基于压缩进步驱动的好奇⼼框架下的⼀个副产品。他们都在努⼒创造新的、⾮随机的、有规则的数据,这些数据中蕴含着令⼈惊叹的、前所未知的规律性。
举个例⼦,许多物理学家会设计实验来创造受未知规律⽀配的数据,以此来进⼀步压缩这些数据。⽽艺术家们则以⼀种主观新颖的⽅式组合已知对象,使得观察者对结果的主观描述,⽐单独描述每个部分要来得简洁,这是因为这些部分共享了⼀些先前未被注意到的规律性。
那么,科学和艺术的主要区别是什么呢?科学的本质,在于正式地界定通过发现新规律⽽实现的压缩进展。⽐如,引⼒定律可以⽤寥寥数个符号来表达。然⽽在美术领域,通过观察将原本不相⼲的事物以新⽅式结合的艺术作品(艺术作为启发者)所实现的压缩进展,可能是潜意识的,观察者可能⽆法正式描述,但他们能感受到这种进展带来的内在奖励,尽管⽆法确切地说出在这个过程中哪些记忆变得更加主观可压缩。
附录中的框架⾜够正式,可以在计算机上实现我们的原则。由此产⽣的⼈⼯观察者,其历史压缩器和学习算法的计算能⼒各有不同。这将决定对他们⽽⾔,什么是好的艺术或科学,以及他们认为什么有趣。
2.16 笑话和其他娱乐资源
喜剧演员,就像其他艺术家⼀样,喜欢将那些⽿熟能详的概念以⼀种新奇的⽅式融合在⼀起。这样⼀来,观众对整体的感受描述,⽐单独描述每个部分来得简洁,原因是这些部分之间存在⼀些之前未曾注意到的共同规律。
机智的笑话所引发的笑声,和婴⼉及成⼈在学习新技能时的笑声,在很多⽅⾯是相似的。⽐如说,我在25岁之后学会了抛接三个球。这并⾮⼀蹴⽽就的过程,⽽是⼀个渐进且令⼈感到满⾜的旅程:起初,我只能持续⼀秒钟,然后是两秒、四秒,逐渐进步,直⾄成功。按照杂耍教练的建议,我在镜⼦前练习,每次取得进步时,我的脸上都会不⾃觉地露出⼀抹傻笑。同样,当我的⼩⼥⼉第⼀次独⽴站⽴时,她也是⼀脸的得意笑容。
在算法的视⻆下,这些现象都能找到合理的解释:这些笑容可能是因为我们⼤脑内部的奖励机制被触发了,它奖励我们⽣成了包含未知规律的数据流。 ⽐如,观察⾃⼰抛接球的感官体验,这与观察他⼈抛接球的体验截然不同,因此显得格外新颖,⾃然⽽然地带来内在的奖赏,直到我们的⼤脑逐渐适应这⼀新技能。
3. 压缩进展驱动系统的早期具体实现
正如之前所说,预测器和压缩器是紧密相连的。任何传⼊的感官数据流,只要它有可预测的部分,都可以被⽤来提⾼整体的压缩效果。因此,早期关于强化学习的研究[57, 58, 61] 中所描述的系统,实际上已经可以看作是压缩进展驱动实现的典型案例。
3.1 预测误差与奖励(1990 年)
早期的研究[57, 58, 61]提出了⼀种基于循环神经⽹络[115, 120, 55, 62, 47, 78]的预测器,这种预测器本质上是⼀个相当强⼤的计算⼯具,即便是按照今天机器学习的标准来看也是如此。它能够根据之前所有输⼊和动作的历史,来预测包括奖励信号在内的感知输⼊。好奇⼼的奖励与预测器的误差成正相关,这隐含了⼀个乐观的假设:只要预测误差⼤,预测器就有望得到改进。
3.2 通过预测器改进奖励压缩进展(1991 年)
近期的研究进展[59, 60]提醒我们,传统的预测⽅法可能并不适⽤于所有场合,特别是在那些充满不确定性的概率环境中。我们不应该只是盯着预测器的错误不放,⽽应该更多地关注它如何不断进步和⾃我完善。不然,系统就会陷⼊⼀个误区,过度关注那些由于噪⾳、随机性或计算能⼒的限制⽽总是预测不准的部分,这反⽽会阻碍我们提⾼数据的主观可压缩性。
虽然在后续研究[61]中提到的神经预测器在计算能⼒上有所不及,但它却带来了⼀项创新——引⼊了⼀种明确的、能够⾃我适应的预测器改进模型。这个模型的核⼼功能就是学会预测预测器⾃⾝的变化。
举个例⼦,尽管外界的噪⾳是⽆法预测的,它会导致预测器的⽬标信号出现剧烈波动,但从⻓远来看,这些波动并不会对⾃适应预测器的参数造成太⼤的影响。⽽预测器变化的预测器,正是通过学习这些变化,来不断提⾼⾃⼰的预测能⼒。
此外,⼀种标准的强化学习算法[114, 33, 109]也被引⼊进来,它通过接收与预期的⻓期预测器变化成正⽐的好奇⼼奖励信号,努⼒在给定的限制条件下最⼤化信息增益[16, 31,38, 51, 14]。实际上,我们可以这样理解:这个系统实际上是在尝试最⼤化数据主观可预测性的预期⼀阶导数的折现总和的近似值,这同时也意味着它在最⼤化数据主观可压缩性的预期变化的折现总和的近似值。
3.3 智能体先验与后验相对熵的奖励机制(1995年)
在1995年的研究中,⾮确定性世界下衍⽣出了⼀种基于信息论的⽅法。这种好奇⼼奖励机制再次与预测器的惊讶度或信息增益同步,这次是通过Kullback-Leibler距离来衡量——即学习预测器在新观察前后主观概率分布的差异,也就是先验与后验之间的相对熵。
到了2005年,Baldi和Itti将此⽅法命名为“⻉叶斯惊奇”,并通过实验验证,它在解释⼈类视觉注意⼒的模式上,⽐之前的⽅法更胜⼀筹。
值得⼀提的是,Huffman编码和先验与后验之间的相对熵概念,可以⽴刻转化为衡量学习进度的指标——反映节省的⽐特数,这是数据压缩改进的⼀种度量。
请注意,虽然简单的概率⽅法在数据压缩上很有⽤,但它不能揭⽰更深层次的算法可压缩性。⽐如,数字 π 的⼗进制展开看起来像是随机的,似乎⽆法压缩,但实际上并⾮如此。有⼀个简短的算法可以计算出 π 的所有数字。
然⽽,任何有限的数字序列在 π 的展开中出现的频率,和 π 的真正随机序列的预期频率是⼀样的。换句话说,没有⼀个简单的统计学习器,能够仅凭之前数字的有限观察,就⽐随机猜测更准确地预测下⼀个数字。我们需要更通⽤的程序搜索技术,⽐如[36, 75, 15, 46],来挖掘潜在的算法规律。
3.4 算法实验揭⽰的零和奖励博弈中的压缩进展(1997年)
近年来的学术研究[68,72](1997年),通过将控制器和预测器设计为共同进化的对称对⽴模块,显著提升了它们的计算能⼒。这些模块基于⼀种⾃适应的、概率性的程序[97,98],使⽤⼀种通⽤编程语⾔[18,111]编写,⽀持循环、递归和层次结构。程序内部的存储空间被视为环境变化的⼀部分,⽤于临时存储计算结果。每个模块都能提出实验性的算法,并以“下注”的形式对其结果进⾏预测,这⾥的“赌注”实际上充当了内在的激励机制。⽽对⽴的模块则可以通过相反的预测来接受或拒绝这种赌注,形成⼀场零和游戏。
⼀旦接受赌注,算法实验的执⾏结果将决定胜者,并且“赌⾦”将从输家转移到赢家⼿中。两个模块都试图利⽤⼀种为复杂随机策略设计的通⽤强化学习算法[97,98]来最⼤化⾃⼰的收益(当然,也可以根据需要插⼊其他类型的强化学习算法)。这促使两个模块不断探索新的算法规律和压缩性,其中新颖性的标准由对⼿对世界重复规律的了解程度来界定。
这种⽅法可以被看作是通过可计算模型和测试的共同进化来进⾏系统识别的过程。到了2005年,Bongard和Lipson[11]采⽤了⼀种基于不那么通⽤的模型和测试的类似共同进化⽅法。
3.5 提升真实奖励的获取
上述⽂献通过实验证实,内在的奖励或好奇⼼驱动的奖励实际上可以加快我们获取外部奖
励的速度。
3.6 其他实现⽅式
最近,⼀些研究⼈员对好奇⼼框架进⾏了创新和改进。Singh、Barto 等学者在强化学习的选项框架中实现了好奇⼼,他们直接利⽤预测误差作为好奇⼼奖励,这在第 3.1 节中有所提及。实际上,他们是最早提出“内在奖励”和“内在动机强化学习”这两个概念的⼈。2005 年,在 AAAI 春季研讨会上,有关机器⼈学发展的其他实现⽅式被提出。你可以参考《连接科学》(Connection Science)的特刊了解更多信息。
4. 主观美和它第⼀衍⽣的“趣味性”视觉展⽰
正如前⾯提到的(第3.3节),我们理论的概率版本[108](1995年)能够阐释⼈类视觉注意⼒的某些变化[32](2005年)。同样,我们可以将这种⽅法应⽤于构建包含易于学习规律的图像,再次强调创意艺术家和被动视觉艺术观察者之间的动机并⽆本质差异(第2.14节)。
两者都在创造⼀系列⾏为,这些⾏为带来有趣的输⼊,⽽“趣味性”则是衡量学习进程的指标,⽐如基于先验知识和后验知识之间的相对熵(第3.3节),或者节省下来的编码数据所需的⽐特数(第1节),或者其他类似的⽅法(第3节)。
在这⾥,我们提供⼀些针对⼈类观察者设计的主观美例⼦,并展⽰从低到⾼主观美的学习过程。由于当前书⾯媒介的限制,我们只能使⽤视觉例⼦,⽽不是声⾳或触觉的例⼦。这些例⼦旨在⽀持这样⼀个观点:⽆监督的注意⼒以及艺术家、舞蹈家、⾳乐家和纯数学家的创造⼒,实际上只是他们追求压缩进步的副产品。
4.1 ⼀张简单明了的脸,附带简洁的算法说明
图 1 展⽰了⼀张在⼀些⼈类观察者眼中“美丽”的⼥性⾯孔构造图。这张脸的基本特征遵循 ⼀个极为简单的⼏何模式[69],这种模式可以⽤极少的信息位来定义。
换句话说,通过观察图像(例如,通过⼀系列眼球快速移动)产⽣数据流,在存在这些规律性的情况下更容易被压缩。
尽管在没有⽹格叠加解释的情况下,很少有⼈能⽴刻明⽩这幅画是如何绘制的,但⼤多数⼈确实注意到⾯部特征以某种⽅式相互协调,展现出了规律性。
根据我们的假设,观察者获得的满⾜感来源于有意识或⽆意识地发现这种数据的可压缩性。这张脸在观察者未能发现新的、未知的规律性之前,会保持其吸引⼒。然后,它就会变得乏味,哪怕对于那些认为它美丽的⼈也是如此——正如⽂中多次指出的,美丽与吸引⼒是两个不同的概念。

图 1 展⽰了⼀个 1998 年发表的⼥性⾯孔构造⽅案。⼀些观察者认为这张脸⾮常“美丽”。尽管画⾯中有很多杂乱的细节,⽐如纹理等,没有简短的描述,但基本的⾯部特征,⽐如位置和形状,可以通过⼀个简单的⼏何⽅案来编码,这个⽅案⽐达芬奇和丢勒的古代⾯部⽐例研究还要简单和精确。
这意味着图像中包含了⼀种⾼度可压缩的规律或模式,可以⽤很少的信息位来描述。 观察者可以通过眼球的⼀系列专注运动或扫视来感知这种规律,并有意识或⽆意识地发现输⼊数据流的可压缩性。
那么,这幅画是如何制作的呢?
⾸先,正⽅形的边被划分成若⼲个相等的区间。然后,连接某些区间的边界,形成三个旋转、叠加的⽹格,这些⽹格基于斜率为 1、2 或 3 的线。通过迭代选择两条先前⽣成的、相邻的、平⾏的线,并在它们之间插⼊⼀条与这两条线等距的新线,从⽽得到⽹格的更⾼分辨率细节。
最后,⽹格在垂直⽅向上被压缩了 4 倍。由此产⽣的线条及其交点,以⼀种从构造⽅案中显⽽易⻅的简单⽅式,定义了眉⽑、眼睛、眼睑阴影、嘴巴、鼻⼦和⾯部轮廓的基本边界和形状。
虽然这个⽅案看起来很简单,但实际上很难找到。我之前尝试了数百次,试图在简单的⼏何图形和美丽的⾯孔之间找到如此精确的匹配,但都失败了。
4.2 另⼀幅可以⽤很少⽐特编码的图画
图 2 展⽰了⼀个例⼦:⼀只蝴蝶和⼀瓶插着花的花瓶。这幅画可以⽤很少的信息来描述,因为它可以通过⼀个基于分形圆图案的简单算法来构建——详⻅图 3。
了解这个算法的⼈往往⽐不了解的⼈更欣赏这幅画,因为他们能意识到它的简单性。 但这并不是⼀个简单的、⾮⿊即⽩的过程。
由于⼤多数⼈对圆形有丰富的视觉经验,他们很快就会注意到这些曲线以某种规律的⽅式组合在⼀起。然⽽,很少有⼈能⽴刻说出这幅画背后的精确⼏何原理。这种模式可以从图3 中学到。
从较⻓的数据描述到较短的数据描述,或从较少的压缩到较多的压缩,或从较少的主观感知美到较多的主观感知美,这种有意识或下意识的发现过程带来的奖励,取决于主观美的⼀阶导数,也就是学习曲线的陡度。

图 2 展⽰了⼀幅蝴蝶和插花瓶的图⽚,这张图⽚是引⽤⾃达芬奇的作品[67, 81]。图 3 则向我们展⽰了这幅图⽚是如何构建的,并且解释了为什么它的描述会如此简洁。

图3:图2的构建过程,是通过⼀个利⽤分形圆的极简算法实现的[67]。画框本⾝就是⼀个圆。它最左边的点,同时也是另⼀个同样⼤⼩的圆的中⼼。
每当两个等⼤的圆相切或相交,它们的接触点就会成为另外两个圆的中⼼,这两个新圆的⼤⼩分别是原圆的相等⼤⼩和减半⼤⼩。
画中的每条线,都是某个圆的⼀部分,其端点正是圆与圆相触或相交的地⽅。⼤圆寥寥⽆⼏,⼩圆却星罗棋布。通常来说,圆越⼩,描述它所需的信息位就越多。这幅画之所以简单(易于压缩),是因为它建⽴在少数⼏个较⼤的圆上。
许多观察者表⽰,他们在发现这种简约之美的过程中,体验到了⼀种特别的快乐。观察者的学习过程,使得数据的主观复杂性降低,从⽽带来了主观美感的暂时⾼峰:⼀条陡峭的学习曲线。(我也曾历经⻓时间的探索,才找到了⼀种令⼈满意且有回报的⽅式,利⽤分形圆创作出⼀幅不错的画作。)
5. 结论与未来展望
我们发现,⼀个出⼈意料地简单的算法原理,基于数据压缩和其进展的概念,能⾮正式地阐述注意⼒、新奇、惊讶、兴趣、好奇⼼、创造⼒、主观美感、幽默以及科学和艺术的基本原理。
这个形式化框架的核⼼要素包括:
- ⼀个持续升级的数据历史预测器或压缩器。
- ⼀个可计算的压缩器进展度量,⽤以评估内在奖励。
- ⼀个奖励优化器或强化学习器,它将奖励转化为预期能最⼤化未来收益的⾏动序列。
为了提升我们之前实现这些要素的⽅法(⻅第三部分),我们将:
- 研究更优的⾃适应压缩器,特别是最近出现的新型递归神经⽹络(RNN)和其他通⽤但实⽤的预测⽅法。
- 探讨在何种条件下,可以既准确⼜⾼效地计算学习进展度量,避免频繁且成本⾼昂的对整个历史数据的压缩器性能评估。
- 研究最新改进的强化学习技术在策略梯度、⼈⼯进化等领域的应⽤。
除了打造更先进的强化学习代理,我们还可以通过⼼理学研究来测试我们理论的预测,这将扩展之前的相关研究,并超越那些只能算作轶事的证据。
设计控制实验应该不难,让参与者预测那些最初未知但存在因果联系的事件序列,这些序列可能包含复杂或简单的、可学习的模式或规律。
参与者需要量化他们对改进预测的内在奖励。奖励是否真的在预测改进最快时最强?当预测达到完美或停⽌改进时,内在奖励是否真的消失了?
最后,我们如何通过神经科学来验证我们的预测呢?
⽬前,我们对⼈类神经系统的理解还很有限。但众所周知,某些神经元似乎能够预测其他神经元的活动,⽽⼤脑扫描显⽰某些脑区在接收到奖励时会活跃起来。
因此,上述提到的⼼理学实验应该与神经⽣理学研究相结合,以确定内在奖励的来源,并可能将其与神经预测器的改进联系起来。
这项⼯作的成功,将为我们在机器⼈领域实践我们的理念,注⼊更多动⼒。
附录 A
本附录的内容主要参考了⽂献 [81, 88]。
压缩技术,让我们能更深⼊地理解这个世界。 通过改进⼤数据压缩算法,我们能发现更⾼效的数据处理⽅法。现在,我们要思考的是如何构建⼀个智能系统,它不仅能够获得外部奖励,还能⾃主学习和探索,发现那些易于理解和压缩的数据。(这种通过⾃我探索获得的洞察,最终可能帮助我们更好地完成⽼师布置的任务。)
我们来正式地思考⼀个学习型智能体,它的⽣命由⼀系列离散的时间周期构成,⽤(t=1,2,...,T)来表⽰。智能体的整个⽣命周期(T)可能是预先确定的,也可能不是。在下⾯的讨论⾥,我们⽤(Q(t))来表⽰时间(t)时变量(Q)的值。如果(Q)的值是从时间1到时间(t)的序列,我们记它为(Q(leq t))。
如果序列不包括时间(t)的值,我们记它为(Q(<t))。在每个时间点(t),智能体会从环境那⾥接收到⼀个实数输⼊(x(t)),然后执⾏⼀个可能影响未来输⼊的实数动作(y(t))。在时间(t)还没有达到⽣命周期结束(T)之前,智能体的⽬标是尽可能地最⼤化其未来的成功或效⽤。
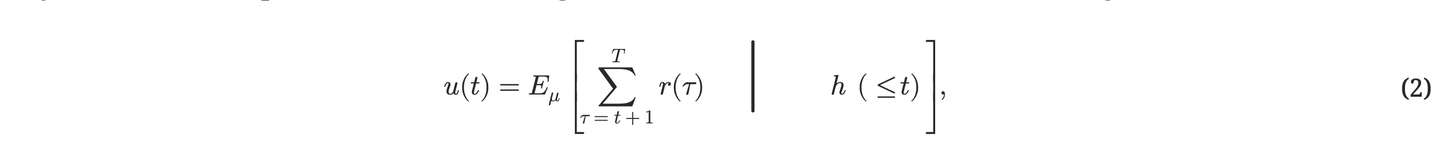
其中,r(t) 代表在特定时刻 t 的额外实际奖励输⼊,⽽ h(t) 是⼀个有序的三元组 [x(t),y(t), r(t)](因此 h(≤t) 就是指到时刻 t 为⽌我们所知道的历史信息)。
Eμ(·|·) 表⽰的是对某个可能未知的分布 μ 的条件期望运算符,这个分布 μ 可能来⾃⼀组可能的分布集合 ℳ。这⾥的 ℳ 反映了我们对环境可能的随机反应的所有已知信息。
打个⽐⽅,ℳ 可能包含了所有我们能计算出来的分布。这⾥我们只有⼀次⽣命的机会,没有预设的重复试验,传感器与环境之间的交互也不局限于⻢尔可夫性质,效⽤函数暗含地考虑了预期的剩余寿命 Eμ(T|h(≤t)),也就是说,通过恰当的⾏动,我们还有延⻓寿命的可能性。
最新的研究进展已经催⽣了第⼀批在多种⾮常⼴泛的意义上都具有普适性和最优化的学习机器。正如在引⾔中提到的,这些机器理论上可以⾃⼰判断好奇⼼和构建世界模型在特定环境中是否有⽤,然后据此调整⾃⼰的⾏为。
不过,本附录将会先验地假定历史压缩或解释是有益的,并且应该进⾏。我们暂时不会考虑好奇⼼可能带来的害处。
为了实现这⼀⽬标,秉承我们⾃1990年以来⼀贯的研究精神,我们将奖励信号 r(t) 分解为两个标量的实值部分:r(t) = g(r_ext(t), r_int(t)),其中 g 是⼀个将实数值对映射到实数值的函数,例如 g(a, b) = a + b。
这⾥的 r_ext(t) 指的是环境提供的传统外部奖励,⽐如撞到墙时的负⾯奖励,或者达到某个由教师指定的⽬标状态时的正⾯奖励。
但对于本⽂来说,我们特别关注的是 r_int(t),也就是内部的、内在的或者可以说是好奇⼼驱动的奖励,这种奖励会在代理的数据压缩器或内部世界模型在某种可测量的⽅式上得到提升时提供。我们最初的关注点将是 r_ext(t) = 0(对所有有效的 t)。这个基本原理本质上是我们之前以不同变体发表过的内容:
原理1
当预测器或历史压缩器得到改进时,就为控制器⽣成好奇⼼奖励。
所以,我们⾸先要在思想上把⽬标(也就是解释和压缩历史)和实现⽬标的⽅法区分开来。⼀旦我们清晰地将⽬标定义为⼀种计算好奇⼼奖励的算法,接下来就交给控制器的强化学习(RL)机制去搞定。这个机制要想办法把这些奖励转化为⼀系列⾏动步骤,让现有的压缩器改进算法能够发现并利⽤那些我们之前从未意识到的可压缩性类型。
A.1 预测器与压缩机
我们以前在强化学习⽅⾯的许多⼯作是以预测为导向的,例如: [57, 58, 61, 59、60, 108, 68, 72, 76] 。 不过,预测和压缩是密切相关的。 ⼀个能正确预测 许多 x(τ) , 给定历史 h(<τ) , 对于 1≤τ≤t 、 可⽤于对 h(≤t) 进⾏紧凑编码。
给定预测因⼦后,只有错误预测的 x(τ) 加上 有关 相应的时间步⻓ τ 是必要的 来重建历史 h(≤t) ,例如,[63]. 同样,⼀个预测器可以学习到 在给定前⼀个事件的情况下,可能发⽣的下⼀个事件可⽤于 对预测概率⾼(分别为低)的观测结果进⾏有效编码 [28,95]⼏位(分别为多位),从⽽实现压缩历史表⽰法。
⼀般来说,我们可以把预测器看作是程序 p ,重新计算 h(≤t) 。 如果该程序与原始数据 h(≤t) 相⽐较短,那么 h(≤t) 是有规律的还是⾮随机的 [106, 34, 37, 73] 、 ⼤概反映了基本的环境法。然后 p 也可能对预测未来⾮常有⽤。 x(τ) 为 τ>t 。
然⽽,应该提到的是,基于最⼩描述⻓度(MDL)原则的⾯向压缩器的预测⽅法 [34, 112, 113, 54,37] 不⼀定像所罗⻔洛夫的普遍归纳推理那样迅速收敛到正确的预测 [106,107, 37], 虽然这两种⽅法在⼀般条件下都会在极限收敛 [52]。
A.2 哪个预测器或历史压缩器?
对某些压缩机 p 进⾏评估的复杂性历史 h(≤t) 取决于 p 及其性能 测量 C 。让我们⾸先关注前者。 给定 t ,最简单的 p 之⼀是 只需使⽤线性映射 从 x(t) 和 y(t+1) 中预测 x(t+1) 。
更复杂的 p 如⾃适应递归神经⽹络 (RNN) [115, 120, 55, 62、47, 26, 93, 77, 78] 。 将使⽤⾮线性映射 以及整个历史 h(≤t) 作为预测的基础。 事实上,关于强化学习的第⼀部著作[61] 就集中体现了这⼀点。 的在线学习 RNN。 理论上最佳的预测因⼦是所罗⻔洛夫的上述通⽤归纳法 [106, 107, 37]。
A.3 压缩机性能措施
随时 t ( 1≤t<T )、 如果某个压缩程序 p 能够压缩 历史 h(≤t) ,让 C(p,h(≤t)) 表⽰ p 在 h(≤t) 上的压缩性能。 适当的绩效衡量标准是:
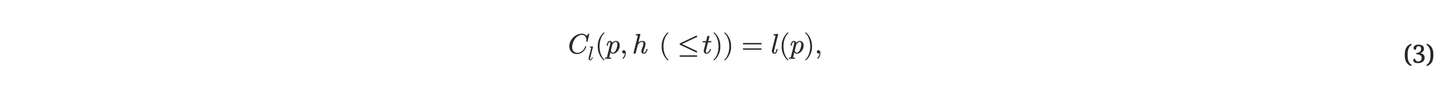
其中 l(p) 表⽰ p 的⻓度,以⽐特数表⽰: p 越短、 算法的规律性和可压缩性越强,以及在迄今为⽌的观察中,我们发现了可预测性和合法性。 Cl(p,h(≤t)) 的最终限制是 K∗(h(≤t)) ,科尔莫哥罗夫复杂性的⼀个变体 的 h(≤t) ,即最短程序的⻓度 (对于给定的硬件),计算输出 从 h(≤t) 开始 [106, 34, 37, 73] 。
A.4 考虑时间因素的压缩机性能指标
Cl(p,h(≤t)) 不考虑时间 τ(p,h(≤t)) 由 p 花费在计算 h(≤t) 上。 受概念启发的另⼀种性能
测量⽅法最佳通⽤搜索的 [36, 75] 是:
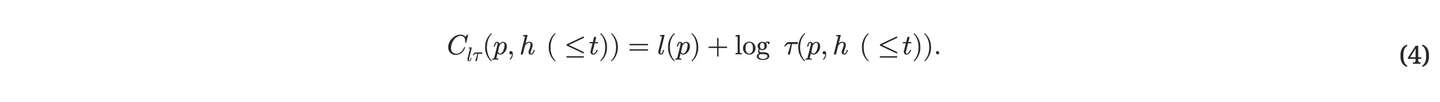
在这⾥,压缩⼀个⽐特的价值等同于运⾏时间减少到原来的1/12。 从以渐进最优性为导向的⻆度来看,这是在存储空间和计算时间之间进⾏权衡的最佳⽅式之⼀[36, 75]。
A.5 压缩机进步/学习进步的衡量标准
前⼏部分内容仅讨论了压缩器性能的衡量标准,但没有讨论性能提升,⽽这正是我们以好奇⼼为导向的背景下的核⼼问题。重申上⾯的观点:重要的不是压缩器的压缩性能本⾝,⽽是其性能的提升。我们对压缩器在时间 t 到 t+1 之间(由于某些依赖于应⽤的压缩器改进算法)所取得的进步的好奇⼼回报应该是:
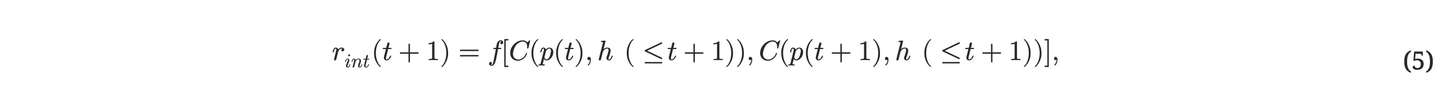
这⾥的( f )是⼀个函数,它将⼀对实数值映射到另⼀个实数值。存在多种可能的衡量进展的替代⽅法;最明显的是( f(a, b) = a - b )。这对应于最⼤化主观数据压缩性的⼀阶导数的离散时间版本。简单来说,就是通过计算连续两次测量值之间的差值来衡量压缩器性能的进步。
请注意,新旧压缩机都必须在相同的数据(即迄今为⽌的历史数据)上进⾏测试。
A.6 创建好奇⼼奖励的异步框架
让 p(t) 表⽰代理在时间 t 时的当前压缩机程序、 s(t) 其当前控制器,并执⾏:
控制器:在 t ( 1≤t<T ) 的任何时候都要这样做:
- 让 s(t) 使⽤(部分)历史 h(≤t) 来选择并执⾏ y(t+1) 。
- 请注意 x(t+1) 。
- 检查是否存在⾮零好奇⼼奖励 r_int(t+1) 由单独异步运⾏的 压缩机改进算法(⻅下⽂)。 如果没有,则设置 r_int(t+1)=0 。
- 让控制器的强化学习(RL)算法使⽤ h(≤t+1) 。 包括 r_int(t+1) (可能还有最新的观测数据的压缩版本(⻅下⽂)以获得新的控制器 s(t+1) 、符合⽬标(2)。
压缩机:将p_new设置为初始数据压缩器。从时间1开始,不断重复以下步骤,直到在时间T被中断或终⽌:
- 设置 p_old=p_new ; 获取当前时间步⻓ t ,并设置 h_old=h(≤t) 。
- 在 h_old 上对 p_old 求值,得到 C(p_old,h_old) (第 A.3 节)。这可能需要很多时间步骤。
- 让我们考虑某个(与应⽤相关的)压缩器改进算法,例如⼀个⽤于⾃适应神经⽹络预测器的学习算法。这个算法利⽤当前的压缩器(称为h_old)来获得⼀个希望更好的压缩器p_new,例如⼀个具有相同⼤⼩但预测能⼒更强、因此压缩性能也更好的神经⽹络[95]。尽管这个过程可能需要很多时间步(并且在“休眠”期间可能部分完成),但由于学习算法的限制,⽐如可能会陷⼊局部最⼤值,p_new可能并不是最优的。
- 在 h_old 上求值 p_new ,得到 C(p_new,h_old) 。 这可能需要很多时间步骤。
- 获取当前时间步⻓ τ 并⽣成好奇⼼奖励。
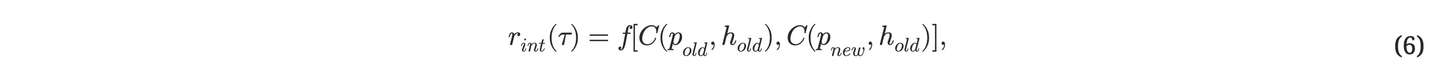
例如,f(a,b)=a−b;⻅第A.5节。
显然,这种异步⽅案可能会导致控制器操作与相应的好奇⼼奖励之间出现较⻓的时间延迟。这可能会给控制器的强化学习算法带来沉重负担,因为该算法的任务是为过去的⾏动分配信⽤(为了让控制器了解压缩机评估过程等的开始,我们可以通过此类事件的独特表⽰来增加其输⼊)。不过,有⼀些强化学习算法在不同意义上都是理论上最优的,我们将在下⽂中讨论。
A.7 最佳好奇⼼、创造⼒和专注⼒
我们选择的压缩机级别通常有 某些计算上的限制。在没有任何外部奖励的情况下、 我们可以定义相对于这些限制的最佳纯好奇⼼⾏为: 在时间 t 时,该⾏为会选择能最⼤化:
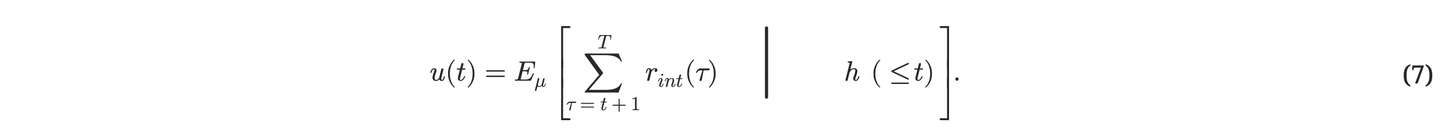
由于真实的、⽀配世界的的概率分布 μ 是未知的,因此控制器的强化学习算法⾯临的任务可能是⾮常艰巨的。当系统重新访问环境中之前⽆法压缩的部分时,这些部分中的⼀些将趋于变得更容易主观上进⾏压缩,相应的好奇⼼回报会随着时间减少。
⼀个好的强化学习算法必须能够检测到这种减少,并预测它,然后据此采取⾏动。然⽽,传统的强化学习算法[33]并没有为这种情况提供任何理论上的最优性保证。(这并不是说次优的强化学习算法在某些应⽤中可能不会导致成功;实验研究可能会带来有趣的洞⻅。)
⾸先,我们做⼀个⾃然的假设:压缩器不是像柯尔莫哥洛夫复杂度那样的超复杂系统,也就是说,它的输出和rint(t)对于所有的 t 都是可以计算的。那么问题来了,是否存在⼀种最佳的强化学习算法,它能像其他任何算法⼀样接近最⼤化⽬标(7)的值呢?确实存在这样的算法。然⽽,它的缺点是它不能在有限的时间内计算出来。尽管如此,它作为⼀个参考点,定义了什么是最佳可达到的性能。
A.8 最佳但不可计算的⾏动选择器
有⼀种选择⾏动的最佳⽅法 它利⽤了所罗⻔夫理论上最优的 通⽤预测器及其⻉叶斯学习算法 [106, 107, 37, 29, 30] . 后者只是假设环境中的反应取样于 ⼀个未知概率分布 μ 包含在⼀个集合 ℳ 中 的所有可数分布⽐较等式后的⽂本(2 )。 更确切地说,给定观测序列 q(≤t) 。 我们唯⼀的假设是,存在⼀个计算机程序 它可以将任何 q(≤t) 作为输⼊,并计算其先验概率 μ 先验值。 ⼀般来说,我们不知道这个程序,因此 我们改⽤混合先验进⾏预测:
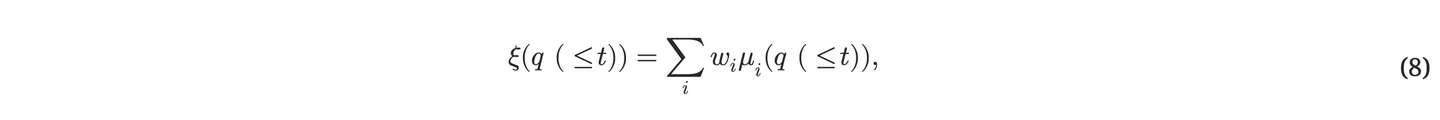
所有分布 μi∈ℳ 、 i=1,2,… 的加权和、 其中常数正权重之和满⾜ ∑_i w_i ≤ 1 。 从⼀般意义上讲,这确实是我们能做的最好的事情了 [107, 29].缺点 由于 ℳ 中包含了⽆穷多的分布。 我们可以通过以下⽅法提⾼该⽅案的理论威⼒ 通过某些⽅法增强 ℳ 。 但 可极限计算的分布 [73]、 或对其进⾏限制,使其变得可计算、 例如,假设世界是计算出来的 由某个未知但确定的计算机 [74]中采样的程序,该程序分配了 对任何⽅法都难以计算的环境⽽⾔,概率较低。
⼀旦有了这样⼀个最佳预测器,我们就可以对其进⾏扩展 通过正式纳⼊已执⾏操作的效果来定义⼀个 最⼤化未来预期回报的最优⾏动选择器。 在任何时候, t ,哈特的理论最佳值都是 (尚⽆法计算的)强化学习算法 Aixi [29] 使⽤所罗⻔夫预测⽅案的扩展版本 以选择那些能带来最⼤收益的⾏动序列 在当前数据 h(≤t) 的条件下,未来的奖励直⾄某个跨度 T 。
也就是说,在周期 t+1 中,Aixi 选择动作序列的第⼀个动作作为下⼀个动作 最⼤化 ξ 在给定时间范围内的预测回报,适当地 概括公式 (8). 艾溪优化使⽤观测[29] : ⻉叶斯最优策略 pξ 基于 ξ 混合物是⾃我优化的,因为它的平均值为 对于所有 μ∈ℳ 来说,效⽤值都会逐渐趋同于 ⻉叶斯最优策略实现的最优值 pμ 提前知道 μ 。必要条件和充分条件是 ℳ 承认⾃我优化策略。 政策 pξ 也是帕累托最优的 从这个意义上说,没有其他政策能产⽣更⾼或同等的结果。 所有环境 ν∈ℳ 中的值,以及严格意义上的更⾼值。 ⾄少⼀个 [29] 中的值。
A.9 可计算的可证明最优⾏动选择器
上述 Aixi 需要⽆限的计算时间。它的可计算变体 Aixi(t,l) [29] 具有渐近最优的运⾏时间,但可能会出现巨⼤的持续减速。为了以⼀般的最优⽅式将消耗的计算时间考虑在内,我们可以使⽤最近的哥德尔机 [79, 82, 80, 92] 来代替。它们代表了第⼀类数学上严谨、完全⾃反、⾃改进、通⽤、最优效率的问题求解器。它们也适⽤于⽬标 (7) 所体现的问题。
这种哥德尔机器的初始软件 𝒮 包含初始问题解决者,例如⼀些典型的次优⽅法 [33]. 它还包含⼀个渐进优化的初始证明基于莱⽂的在线变体的搜索器 Universal Search [36]、 ⽤于运⾏和测试证明技术。
证明技术是⽤通⽤语⾔编写的程序 𝒮 内的哥德尔机器上。它们原则上能够计算证明关于系统⾃⾝的未来性能,基于公理的 系统 𝒜 以 𝒮 编码。 𝒜 描述了正式的效⽤函数,在我们的例⼦中是公式(7 )、 硬件特性、算术和概率公理 理论和数据操作等,以及 𝒮 本⾝,这是可能的 不引⼊循环 [92].
受库尔特·哥德尔(Kurt Gödel)著名的⾃反公式(1931 年)启发、哥德尔机器通过⾃⽣成的可执⾏程序重写其⾃⾝代码的任何部分(包括证明搜索器),只要其Universal Search变体根据⽬标(7)找到重写是有⽤的证明。根据全局最优定理 [79, 82, 80, 92],这样的⾃重写是全局最优的,不可能出现局部最⼤值!-因为⾃引⽤代码⾸先必须证明,继续寻找其他⾃改写是没有⽤的。
如果没有可证明的最佳 𝒮 的重写⽅式,那么⼈类也找不到。但如果有的话那么 𝒮 本⾝就可以找到并利⽤它。与以往基于硬连线证明搜索器的⾮⾃我指涉⽅法[29] 不同、 哥德尔机器不仅拥有最佳的复杂度阶次,还能以最佳⽅式减少(通过⾃我更改) O() 注释所隐藏的任何减速,前提是实⽤程序是可以证明的。⽐较 [83, 86, 85]。
A.10 ⾮通⽤但仍通⽤且实⽤的强化学习算法
最近,强化学习算法取得了重⼤进展,这些算法不像上述算法那么通⽤,但却能够学习⾮常通⽤的、类似程序的⾏为。
特别是,进化⽅法 [53, 99, 27] 可⽤于训练循环神经⽹络(RNN),这是⼀种通⽤计算机。[40, 122、121, 45, 39, 103, 42] 。
⼀个特别有效的⽅法系列使⽤合作协同进化来搜索⽹络组件(神经元或单个突触)的空间,⽽不是完整的⽹络。共同进化的⽅式是将这些组件组合成⽹络,并选择那些参与性能最佳网络的组件进行繁殖[43, 20, 21, 19, 22, 24] 。
最近⽤于 RNN 的其他 RL 技术基于策略梯度的概念 [110,119, 118, 56, 100, 117] .在好奇⼼奖赏框架内对此类控制学习算法的变体进⾏评估将很有意义。
A.11 致谢
感谢 Marcus Hutter、Andy Barto、Jonathan Lansey、Julian Togelius、Faustino J.Gomez、Giovanni Pezzulo、Gianluca Baldassarre、Martin Butz 的宝贵意⻅,这些意⻅帮助改进了本⽂的第⼀个版本。