控制之美1-第七章 PID控制

目录

• 7.1 引子
• 7.2 比例控制

7.1 引子

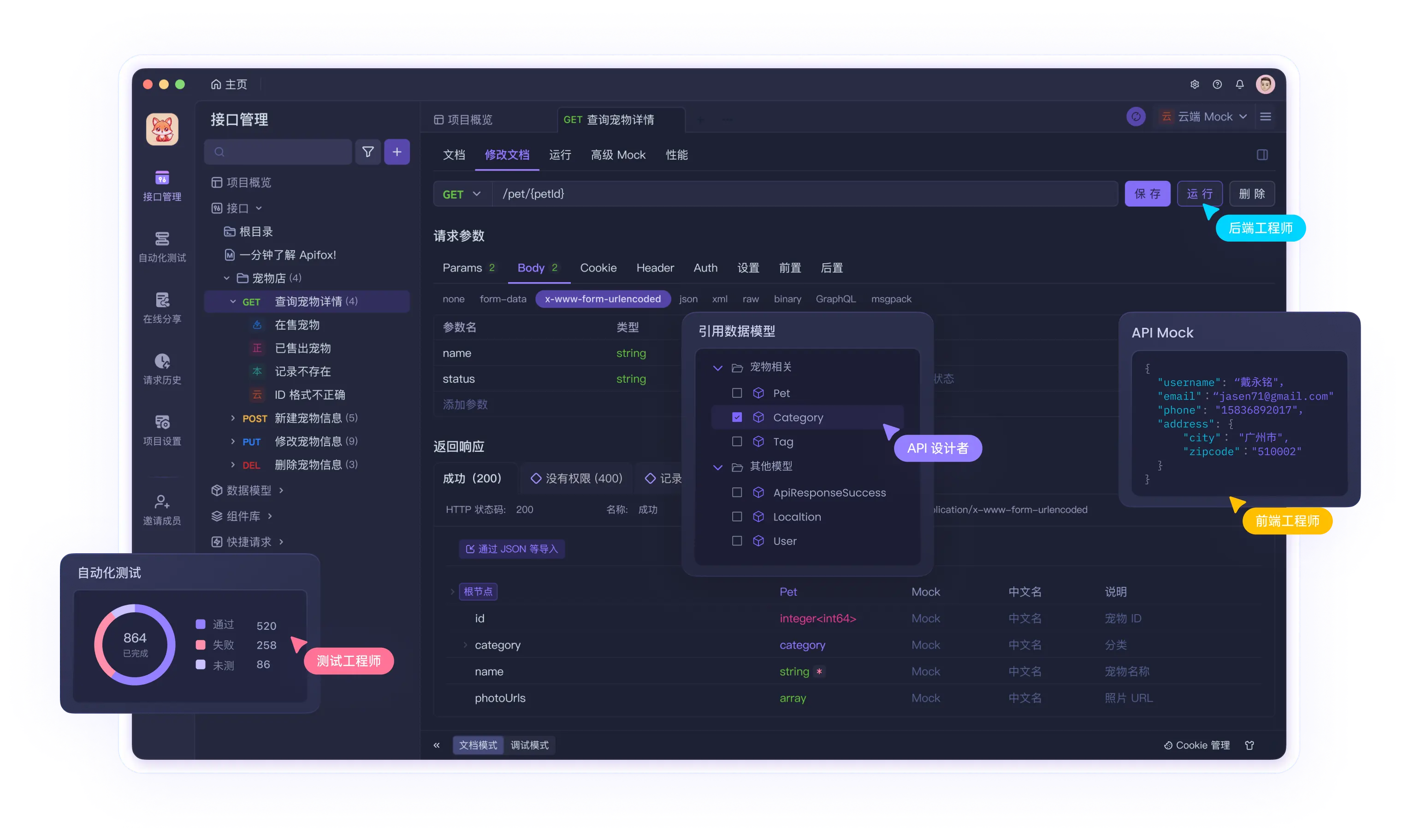
\[7000 \frac{dx(t)}{dt}+10ax(t)=u(t)+d(t) \]

\(u(t)\) 是体重变化，

\(u(t)=E_i-E_a\), \(E_i\) 是热 量摄入 ,\(E_a\) 是运动消耗,

\(x(t)\) 系统输出，体重

\(a\)是劳动强度系数

\(d(t)=-aC\) 是扰动量

进行拉普拉斯变换

\[7000(sX(s)-x_0)+10asX(s)=U(s)+D(s) \]

\[→ (7000s+10a)X(s)=U(s)+D(s)+7000ax_0 \]

\(x_0\) 是初始体重，

传递函数

\[G(s)=\frac{X(s)}{U(s)+D(s)+7000x_0}=\frac{1}{7000s+10a} \]

其中\(U(s)\) 和 \(D(s)\)是以 阶跃形式作用在系统上 ，
初 始状态\(7000x_0\),则是以 冲激方 式作用 在系统上。

\(G(s)\) 的特征方程为

\[7000s + 10a =0 \]

\[s_p= -\frac{a}{100}<0 \]

7.2 比例控制

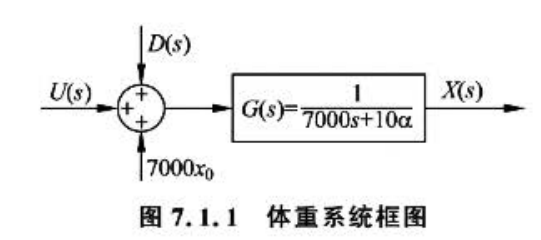
r(t)是目标体重(参考值)，r(t)=r=65kg,对应的拉普拉斯变换\(R(s)=\frac{r}{s}\)

\(e(t)=r(t)-x(t)\)是误差（参考值与输出之家的差距），对应的拉普拉斯变换\(E(s)=R(s)-X(s)\)

\(C(s)\)是控制器，包含了我们需要设计的算法

人们在控制体重时会很自然地想到一种 策略-当体重大于目标值的时候， 那就多运动.
少吃饭 ，而且超重得越多 ，就越要多运动， 越要少吃饭， 反之亦然。 这 种简单粗暴的策略被
称为比例控制( Proportionz Controller) .

比例控制是一种简单的控制方式，其控制量为误差的线性函数：

\[u(t)=K_{P}e(t) \]

\(K_{P}\) 为比例增益， $ e(t)$ 为误差。

在拉普拉斯变换域中，比例控制可以表示为：

\[U(s)=K_{P}E(s) \]