P10304 [THUWC 2020] 道路修建

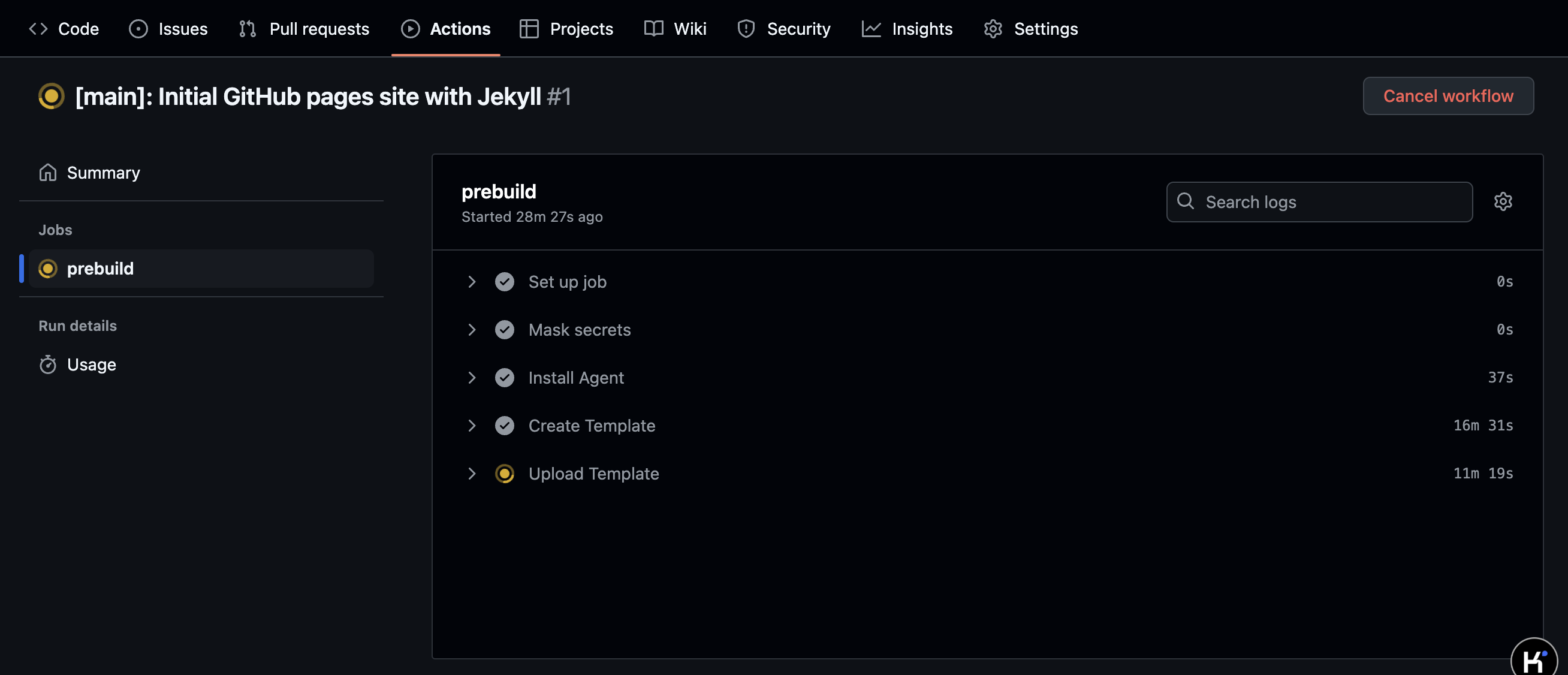
注意到 \(1\) 到一个 \(b\) 子树内的点 \(x\) 的路径可以拆成 \(1\to p\to q\to x\) 的形式，其中 \(1\to p\) 走树边，\(p\to q\) 为在点 \(p\) 从树边走出去，在点 \(q\) 走回来，然后 \(q\) 再走树边走到 \(x\)。

考虑 \(f_i\) 为最小的 \(d\)，满足断掉 \(i\) 深度为 \(d\) 的祖先到 \(i\) 的链后，\(1\) 仍然能到 \(i\)。那么一个点 \(x\) 能到达当且仅当存在 \(q\) 在 \(b\to x\) 路径上，且 \(f_q\le dep_a\)，即 \(\min\limits_{q\in path(b,x)}f_q\le dep_a\)。

考虑怎么求 \(f\)。这个可以按照拓扑序从小往大枚举 \(u\)，同时处理所有非树边 \(u\to v\)，贡献为 \(u\) 到 \(\operatorname{LCA}(u, v)\) 这条链上 \(f\) 的最大值。因为此时 \(u\to \operatorname{LCA}(u, v)\) 链上的 \(f\) 都已知，可以直接倍增。

现在我们已知了 \(f\)，把每组询问挂在 \(b\) 上，动态维护 \(\min f\) 的权值线段树，不难线段树合并做到 \(O((n+m+q)\log n)\)。

code

#include <bits/stdc++.h>
#define ALL(x) begin(x), end(x)
using namespace std;
void file() {freopen("1.in", "r", stdin);freopen("1.out", "w", stdout);
}
using ll = long long;
using PII = pair<int, int> ;const int kInf = 1e9;
const int kN = 1.5e5 + 5;int n, m, q;
array<int, kN> fa, ord, in, dep, f, ans;
array<bool, kN> intr, vis;
array<PII, kN> ed;
array<vector<PII>, kN> g, qry;
array<vector<int>, kN> tr, buc;
array<array<int, kN>, 20> jp, mn;void toposort() {for(int i = 1; i <= m; i++)in[ed[i].second]++;queue<int> q;for(int i = 1; i <= n; i++)if(!in[i]) q.push(i);int tot = 0;while(q.size()) {int x = q.front(); q.pop();ord[++tot] = x;for(auto k : g[x]) {int to = k.first;if(!--in[to]) q.push(to);}}
}void build() {for(int i = 1; i <= n; i++)sort(ALL(g[i]), greater<> ());dep[0] = -1;for(int i = 1, x = 1; i <= n; i++) {vis[x] = 1;for(bool flag = 0; x; x = fa[x]) {while(g[x].size()) {auto k = g[x].back(); g[x].pop_back();int to = k.first;if(vis[to]) continue;else {intr[k.second] = flag = 1;f[to] = dep[to] = dep[x] + 1, fa[to] = x;tr[x].push_back(to), x = to;break;}}if(flag) break;}}
}void init(int x) {mn[0][x] = f[x];for(int i = 1; i < 19; i++)mn[i][x] = min(mn[i - 1][x], mn[i - 1][jp[i - 1][x]]);
}
int lca(int x, int y) {if(dep[x] < dep[y]) swap(x, y);for(int i = 19; ~i; i--)if(dep[jp[i][x]] >= dep[y]) x = jp[i][x];if(x == y) return x;for(int i = 19; ~i; i--)if(jp[i][x] ^ jp[i][y])x = jp[i][x], y = jp[i][y];return fa[x];
}
int query(int anc, int x) {int ans = f[anc];for(int i = 19; ~i; i--)if(dep[jp[i][x]] >= dep[anc])ans = min(ans, mn[i][x]), x = jp[i][x];return ans;
}const int kS = 5e6 + 5;struct SGT {int tot = 0;array<int, kN> root;array<int, kS> ls, rs, sum;void pu(int o) { sum[o] = sum[ls[o]] + sum[rs[o]]; }void modify(int& o, int l, int r, int x, int v) {if(!o) o = ++tot;sum[o] += v;if(l == r) return ;int mid = (l + r) >> 1;if(mid < x) modify(rs[o], mid + 1, r, x, v);else modify(ls[o], l, mid, x, v);}void erase(int& o, int l, int r, int x, int y) {if((l > y) || (r < x)) return ;if((l >= x) && (r <= y)) return void(o = 0);int mid = (l + r) >> 1;erase(ls[o], l, mid, x, y);erase(rs[o], mid + 1, r, x, y);pu(o);}int query(int o, int l, int r, int x, int y) {if((l > y) || (r < x)) return 0;if((l >= x) && (r <= y)) return sum[o];int mid = (l + r) >> 1;return query(ls[o], l, mid, x, y) + query(rs[o], mid + 1, r, x, y);}int merge(int x, int y, int l, int r) {if(!x || !y) return x + y;sum[x] += sum[y];if(l == r) return x;int mid = (l + r) >> 1;ls[x] = merge(ls[x], ls[y], l, mid);rs[x] = merge(rs[x], rs[y], mid + 1, r);return x;}
}sgt;void dfs(int x) {for(int to : tr[x])dfs(to), sgt.root[x] = sgt.merge(sgt.root[x], sgt.root[to], 0, n);int sum = sgt.query(sgt.root[x], 0, n, f[x] + 1, n) + 1;sgt.erase(sgt.root[x], 0, n, f[x] + 1, n);sgt.modify(sgt.root[x], 0, n, f[x], sum);for(auto k : qry[x]) {int dep = k.first, id = k.second;ans[id] = sgt.query(sgt.root[x], 0, n, dep + 1, n);}
}int main() {// file();ios::sync_with_stdio(0), cin.tie(0);cin >> n >> m >> q;for(int i = 1, u, v; i <= m; i++) {cin >> u >> v;ed[i] = PII {u, v};g[u].emplace_back(v, i);}toposort(), build();for(int i = 1; i <= m; i++) {int u = ed[i].first, v = ed[i].second;if(!intr[i]) buc[u].push_back(v);}jp[0] = fa;for(int i = 1; i < 20; i++)for(int j = 1; j <= n; j++)jp[i][j] = jp[i - 1][jp[i - 1][j]];for(auto& k : mn) k.fill(kInf);for(int i = 1; i <= n; i++) {int x = ord[i]; init(x);for(int to : buc[x]) {int anc = lca(x, to);f[to] = min(f[to], query(anc, x));}}for(int i = 1, a, b; i <= q; i++) {cin >> a >> b;qry[b].emplace_back(dep[a], i);}dfs(1);for(int i = 1; i <= q; i++)cout << ans[i] << "\n";return 0;
}