ARC058C. Iroha's Obsession *1174
\(n\) 再大一点的就是巨大恶心分类讨论。但我们注意到 \(n \leq 10^4\),所以我们可以直接暴力枚举然后写个 check。首先我们先把被 ban 掉的数存标记一下。然后从 \(n\) 开始往上查,一直查到 \(10^6\) 基本就可以了。然后每次检查一下有没有数位被 ban 掉,没有的话直接输出然后退出就好了。
#include <bits/stdc++.h>
using namespace std;
int n, k, x;
bool D[11];
int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> k;for(int i = 1; i <= k; i ++) {cin >> x;D[x] = true;}for(int i = n; i <= 1000000; i ++){int ii = i;bool Flag = true;while(ii > 0){if(D[ii % 10]) Flag = false;ii /= 10;}if(Flag) {cout << i << '\n';break;}}return 0;
}
ARC058D. Iroha and a Grid *1905
还算比较经典的组合数学题目。我们注意到 \(n,m\) 非常大,不足以让我们动态规划。但是我们注意到它只 ban 掉一个矩形,于是我们可以考虑分阶段组合计数。
我们先考虑如果没有任何矩形被 ban 掉我们要怎么做。这是简单的,就是 \(\binom{n+m-2}{n-1}\),或者是 \(\binom{n+m-2}{m-1}\),因为由组合恒等式,这两个东西是相等的。
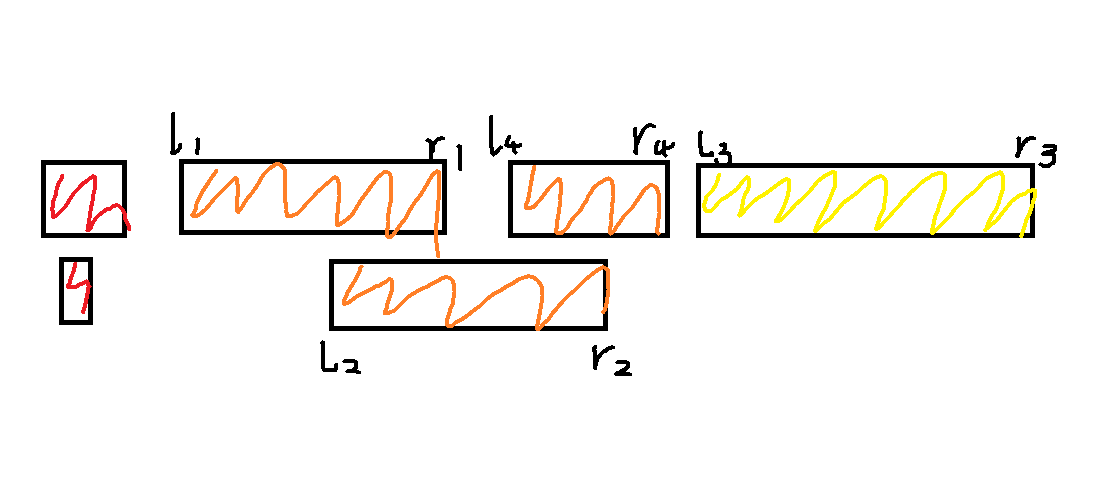
接下来我们考虑它 ban 掉了哪个区域,其实就是 \((n-A+1,1)\) 到 \((n,B)\) 这段区域。那我们考虑把矩阵切了,变为 \((1,1)\) 到 \((n-A,B)\) 和 \((1,B+1)\) 到 \((n,n)\) 这两部分。然后枚举分界点,用乘法原理和加法原理统计它们对于答案的贡献。其实就是
\[\sum_{i=1}^{n-A} \binom{i+B-2}{i-1} \times \binom{n+m-B-i+1}{n-i}
\]
然后就做完了。因为我们需要计算组合数,所以我们可能还需要预处理一步阶乘和阶乘逆元。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MAXN = 200005;
const LL MOD = 1e9 + 7;
LL n, m, A, B, fac[MAXN], inv[MAXN];
LL QuickPow(LL a, LL b, LL p)
{LL res = 1;while(b > 0){if(b & 1) res = (res * a) % p;a = (a * a) % p;b >>= 1; }return res;
}
LL C(LL a, LL b)
{if(a < b) return 0; else return ((fac[a] * inv[b]) % MOD * inv[a - b]) % MOD;
}
LL calc(LL a, LL b) { return C(a + b - 2, a - 1); }
int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m >> A >> B;fac[0] = 1;for(LL i = 1; i <= n + m - 2; i ++) fac[i] = (fac[i - 1] * i) % MOD;inv[n + m - 2] = QuickPow(fac[n + m - 2], MOD - 2, MOD);for(LL i = n + m - 3; i >= 0; i --) inv[i] = (inv[i + 1] * (i + 1)) % MOD;LL ans = 0;for(LL i = 1; i <= n - A; i ++)ans = (ans + (calc(i, B) * calc(n - i + 1, m - B)) % MOD) % MOD;cout << ans << '\n';return 0;
}