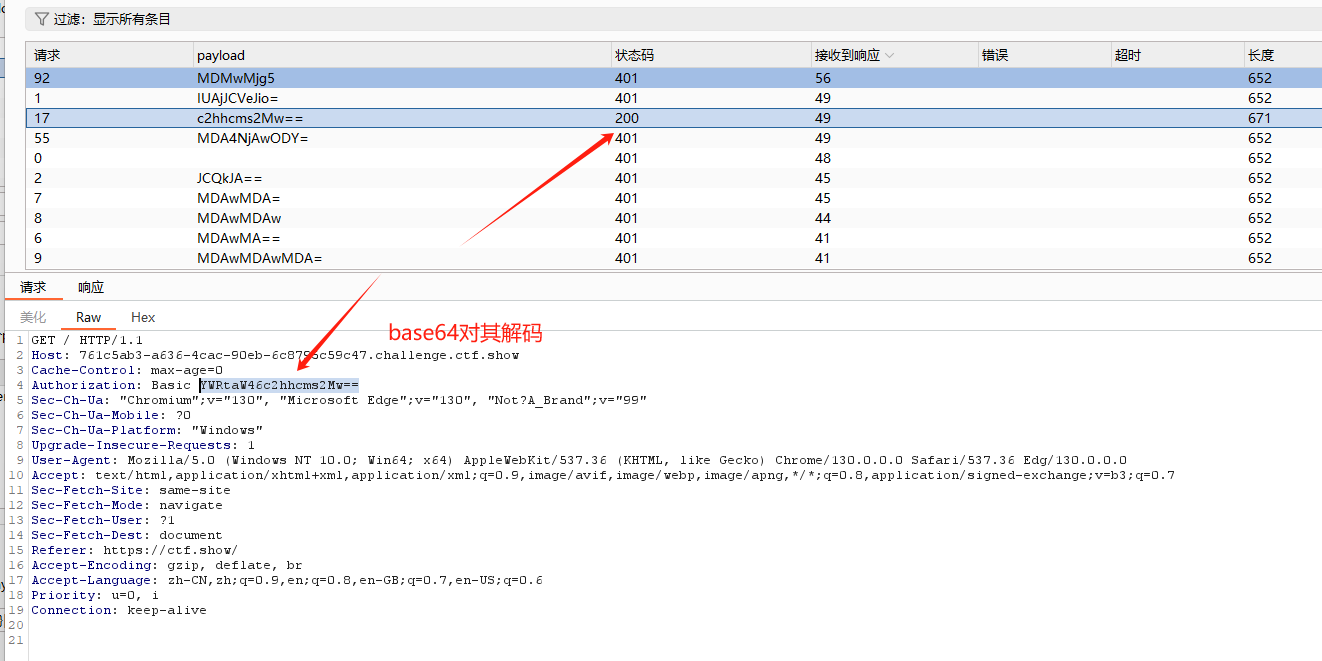
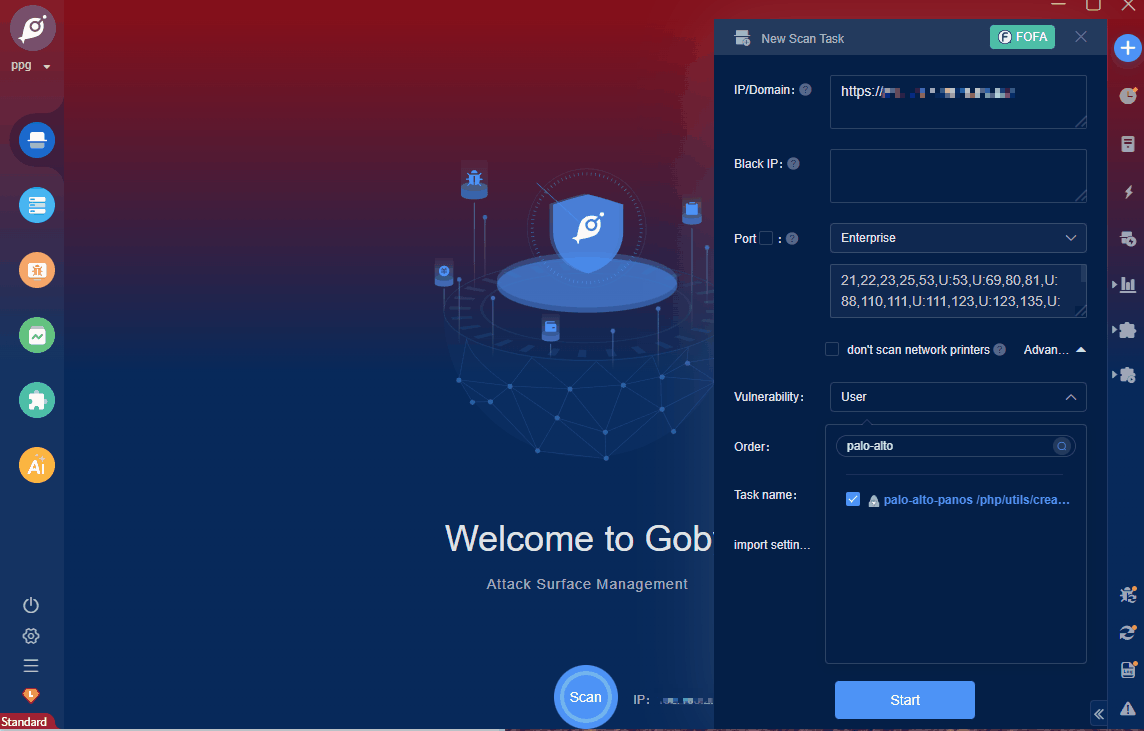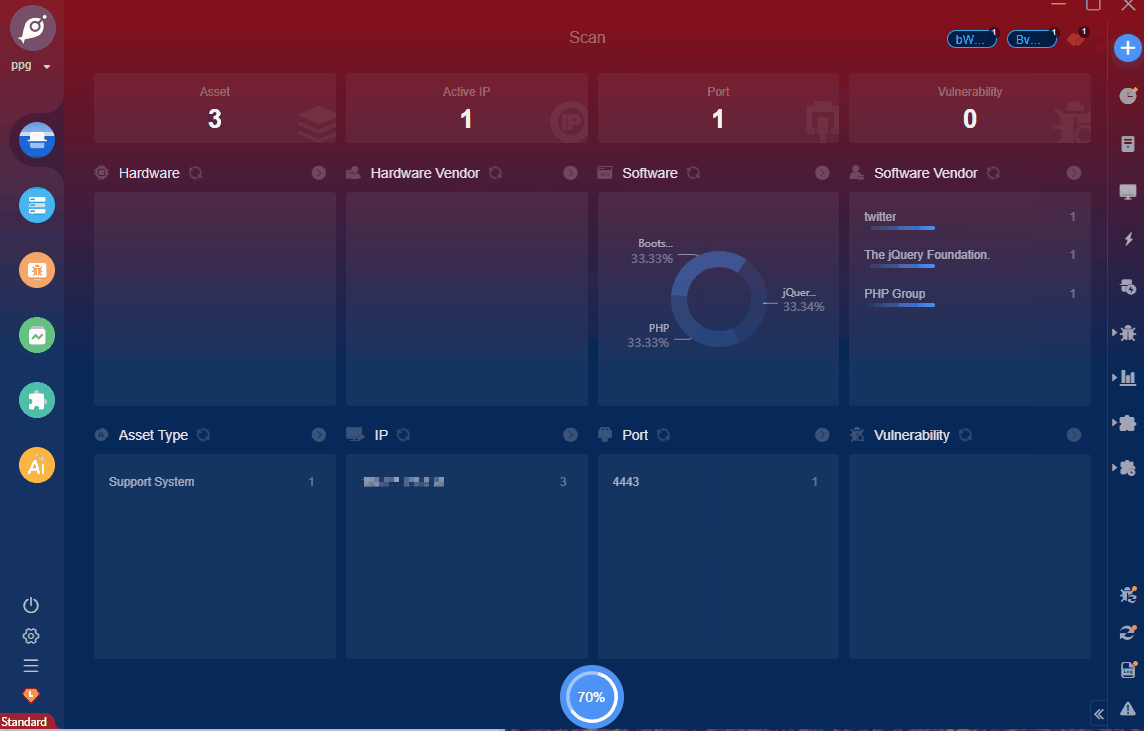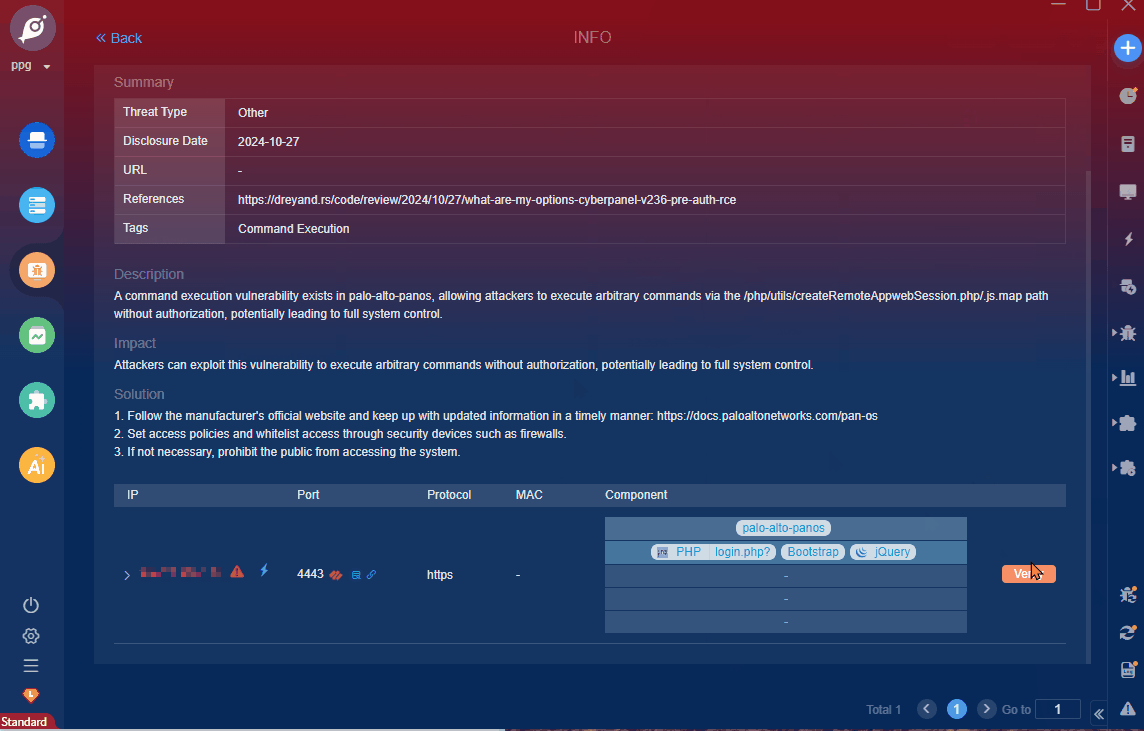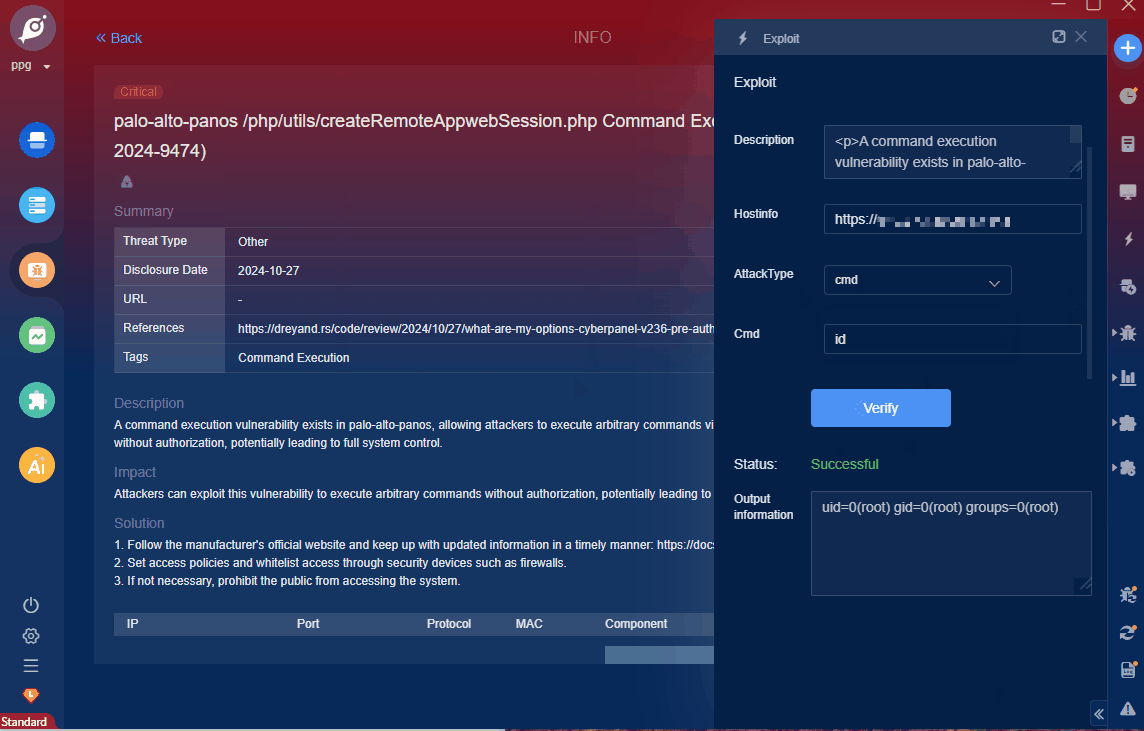
10 days left.
不说闲话,捡重点说。
P4113 [HEOI2012] 采花
hh 的项链加强版。
首先考虑莫队,轻松写,轻松 133pts,轻松过不了后两个 hack,考虑优化。
既然是加强版,那么就考虑沿用之前的思路。记录上次出现某个数的位置和上上次出现某个数的位置,离线之后将询问挂到右端点上,依然是树状数组维护前缀和,我们只用在上上次的位置赋成 1 即可,手模容易理解左端点小于等于这个位置的该颜色一定会有贡献。然后做完了,复杂度 \(\mathcal{O(n\log n)}\)。
P2023 [AHOI2009] 维护序列
其实就是线段树 2。不过还是花了 20min 才切。
难点在 tag 维护。发现分别对加和乘维护 tag 二者是会相互影响的,下放也很不方便。于是直接钦定加的 tag 为最终加算,乘法为直接乘算即可。区间加不需要任何多余操作,区间乘需要同时修改加的 tag,下放时按先乘后加的顺序就做完了。
P4588 [TJOI2018] 数学计算
有些智慧的。
比较一眼出的是直接乘逆元,但是发现互质的影子没有所以求不了一点,于是考虑在操作上维护线段树的区间积。初始值都为 1,遇到乘操作就修改某个位置,遇到除就将某个位置置为 1 即可,答案就是 \(t_1\)。复杂度 \(\mathcal{O(n\log n)}\)。
P5490 【模板】扫描线 & 矩形面积并
感觉是做过最难的扫描线。
做法都写到题面上了,只用考虑怎么维护。对横坐标显然可以离散化,但纵坐标因为要算面积,如果离散化我就不会算了,所以考虑动态开点线段树,线段转到点上做,还是挺轻松的。
但是被控了 20min+,怎么会是呢?原来 1e9 这个小东西是 double 类型的,跟我的其他东西一算就疯狂搞乱我的精度,办法是手写 9 个 0 或者强转类型。
P8865 [NOIP2022] 种花
被签到控了,厉害吧。
思路挺好出的,一列一列扫,维护可行的行的数量。关键在于两个行之间需要隔至少一行。所以考虑暂时记一下上一行的数量,计算完这一行的贡献后再加入。F 就是 C 长了几块,可以同时算。复杂度 \(\mathcal{O(nm)}\)。
P7960 [NOIP2021] 报数
被更简单的题控了,厉害吧。
由于 \(10^7\) 的调和级数算出来是 1.6e8 级别的,所以一直没敢暴力预处理。被控了快 30min 喊来 Abnormal123 一起做,然后啪的一下就过了。每次遇到一个已标记过不合法的数就直接走,否则判断一下是否含有 7,然后枚举倍数标记就行了。最后记得 \(\mathcal{O(n)}\) 处理出来每个数下一个合法数,注意单独处理最后一个数 9999998 的下一个数。
末
总结:上午被硬控,下午线段树。
就不到 10 天了啊,最少可能只会再沉浸式打 8、9 场比赛了,打一场少一场了,且打且珍惜(
还是那句话,拿出自己最好的状态从容面对,欣然接受结果,让它在我们人生中留下一点光,就好啦。
完结撒花~
wkh 的吱吱