洛谷P11290 【MX-S6-T2】「KDOI-11」飞船

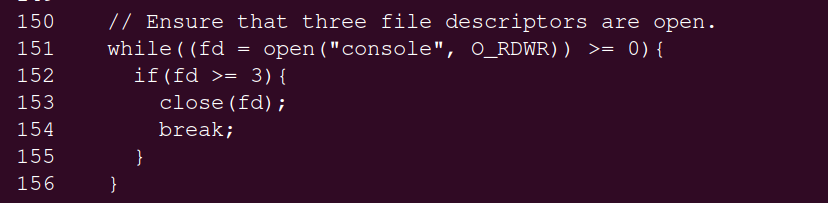
Problem

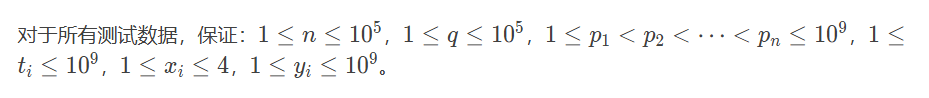
本题开启Special Judge，无需考虑精度问题

Solve

一开始想到这个用DP写，但是不知道怎么定义
去"提交记录"旁边的神秘按钮得知速度可以作为第二维，且类似于背包
那么我们就可以按照背包列出定义 前i个加油站，花费时间j......
但是这里是求最小花费，所以我们要把 类似于最大价值 的速度变成第二维度，但是这样数组开不了，可以进行如下定义
\(f_{i,j,k}\)到第i个加油站，速度为\(2^j\times 3^k\)时的最小用时
注意不要被思维限制了，速度可以作为第二维度!
那这样就好办了，我们每次对于每个状态只需要枚举是否在第i-1个加油站加油就行了
找答案的时候先把询问离线，再等到推出它的前面的加油站时再算上余下路程即可
最后开数组的时候发现开不下，滚动数组优化即可
时间复杂度\(O((n+q)k)\)

这道题的时间卡的有些紧张，常数太大会G，能离线的全部离线
而且存在细节需要多加注意(加上的路程需要考虑此加油站等等...)

Code

#include<bits/stdc++.h>
using namespace std;
int n,q[100005];
map<int,double> ans;
struct p{int p,t,x;
}a[100005];
double f[40][25],g[40][25],pf[40][25];
double ff(int x,int y){double sum=1;for(int i=1;i<=x;i++)sum*=2;for(int i=1;i<=y;i++)sum*=3;return sum;
}
int main(){for(int i=0;i<40;i++){for(int j=0;j<25;j++){pf[i][j]=ff(i,j);}}for(int i=0;i<40;i++){for(int j=0;j<25;j++){f[i][j]=g[i][j]=0x3f3f3f3f;}}scanf("%d%d",&n,&q[0]);for(int i=1;i<=n;i++){scanf("%d%d%d",&a[i].p,&a[i].t,&a[i].x);}a[0]={0,1,1};a[n+1].p=2e9;g[0][0]=0;for(int i=1;i<=q[0];i++){scanf("%d",&q[i]);ans[q[i]]=i;}map<int,double>::iterator it=ans.begin();int a1=2e9,b1=2e9,c1=a1+b1;for(int i=1;i<=n;i++){int u=0,v=0;if(a[i-1].x==1)true;else if(a[i-1].x==2)u=1;else if(a[i-1].x==3)v=1;else u=2;for(int j=0;j<=30;j++){for(int k=0;k<=19;k++){if(pf[j][k]>1e9)break;f[j][k]=min(f[j][k],g[j][k]+(a[i].p-a[i-1].p)/pf[j][k]);if(j>=u&&u){f[j][k]=min(f[j][k],g[j-u][k]+1.0*(a[i].p-a[i-1].p)/pf[j][k]+a[i-1].t);}if(k>=v&&v){f[j][k]=min(f[j][k],g[j][k-v]+1.0*(a[i].p-a[i-1].p)/pf[j][k]+a[i-1].t);}}}memcpy(g,f,sizeof(f));while(it!=ans.end()&&it->first<a[i+1].p){int pos=it->first;double tmp=0x3f3f3f3f;for(int j=0;j<=30;j++){for(int k=0;k<=19;k++){if(pf[j][k]>1e9)break;tmp=min(tmp,f[j][k]+1.0*(pos-a[i].p)/pf[j][k]);tmp=min(tmp,f[j][k]+1.0*(pos-a[i].p)/(pf[j][k]*a[i].x)+a[i].t);}}ans[it->first]=tmp;it++;}for(int j=0;j<40;j++){for(int k=0;k<25;k++){f[j][k]=0x3f3f3f3f;}}}for(int i=1;i<=q[0];i++){if(ans[q[i]]>0)printf("%.8f\n",ans[q[i]]);else cout<<q[i]<<endl;}return 0;
}

此代码的计循环次数能到6e8，总运算次数能达到1e9级别，洛谷神机还是给力的(未开O2能达到约5e8/sec)