- 概
- Gradient Noise Scale
McCandlish S., Kaplan J., Amodei D. and OpenAI Dota Team. An empirical model of large-batch training. 2018.
概
本文讨论了随着 batch size 改变, sgd-style 的优化器的学习应该怎么调整.
Gradient Noise Scale
-
考虑如下的优化问题:
\[\tag{1} \min_{\theta \in \mathbb{R}^D} \quad L(\theta) = \mathbb{E}_{x \sim \rho} [L_x(\theta)], \]其中 \(\rho(x)\) 是数据 \(x\) 所服从的分布.
-
通常来说, 精准地优化 (1) 需要计算整个数据集上的梯度, 这个不太现实, 所以实际中, 通常采用 mini-batch 更新策略:
\[L_{batch}(\theta) = \frac{1}{B} \sum_{i=1}^B L_{x_i} (\theta), \quad x_i \sim \rho. \] -
所对应的, SGD 更新策略为:
\[\theta_{t + 1} \leftarrow \theta_t - \epsilon \underbrace{\frac{1}{B} \sum_{i=1}^B \nabla_{\theta} L_{x_i} (\theta_t)}_{=: G_{est}}, \]其中 \(\epsilon\) 为步长.
-
进一步假设 (\(G = \nabla_{\theta} L, H = \nabla_{\theta}^2 L\))
\[L(\theta - \epsilon V) \approx L(\theta) - \epsilon G^T V + \frac{1}{2} \epsilon^2 V^T H V. \]容易发现, 此时最优的 \(\epsilon\) 为
\[\epsilon_{\max} = \frac{|G|^2}{G^T H G}. \] -
对于 mini-batch 的更新情况, 类似有
\[\begin{array}{ll} \mathbb{E}[L(\theta - \epsilon G_{est})] &= L(\theta) - \epsilon G^T \mathbb{E}[G_{est}] + \frac{1}{2} \epsilon^2 \mathbb{E}[G_{est}^T H G_{est}] \\ &= L(\theta) - \epsilon G^T G + \frac{1}{2} \epsilon^2 \mathbb{E}[G_{est}^T H G_{est}] \\ &= L(\theta) - \epsilon G^T G + \frac{1}{2} \epsilon^2 \mathbb{E}[G^T H G + \frac{\text{tr}(H\Sigma)}{B}], \end{array} \]其中
\[\Sigma = \text{Cov}(\nabla_{\theta} L_x(\theta)). \]
注: 上述第二个等式成立的原因是:
$$
\begin{array}{ll}
\mathbb{E}_x[x^TAx]
&=\mathbb{E}[(A^{1/2} x)^{T} (A^{1/2}x)] \
&=\text{Tr}(\mathbb{E}[(A^{1/2} x)^{T} (A^{1/2}x)]) \
&=\mathbb{E}[\text{Tr}((A^{1/2} x)^{T} (A^{1/2}x))] \
&=\mathbb{E}[\text{Tr}((A^{1/2}x) (A^{1/2} x)^{T} )] \
&=\mathbb{E}[\text{Tr}(A{1/2}xxT A^{1/2})] \
&=\text{Tr}(A^{1/2} \mathbb{E}[xx^T] A^{1/2}) \
&=\text{Tr}(A^{1/2} (\text{Cov}(x, x) + \mathbb{E}[x]\mathbb{E}[x]^T]) A^{1/2}) \
&=\text{Tr}(A \text{Cov}(x, x)) + \mathbb{E}[x]^T A \mathbb{E}[x].
\end{array}
$$
-
因此, 在这个情况下, 我们有
\[\epsilon_{opt} (B) = \frac{\epsilon_{\max}}{1 + \mathcal{B}_{noise} / B}, \quad \mathcal{B}_{noise} = \frac{\text{tr}(H\Sigma)}{G^T H G}. \]其中 \(\mathcal{B}_{noise}\) 被称之为 noise scale.
-
所以, 当 \(\mathcal{B}_{noise} \gg B\) 的时候, 增大 batch size \(B\) 应当相应的线性地增大学习率, 当 \(\mathcal{B}_{noise} < B\) 的时候, 再增大 batch size 对于学习率的调节就不需要那么灵敏 (实际上在这种情况下, 这种情况下再继续增大 batch size 所得到的效率的增益是很微弱的):
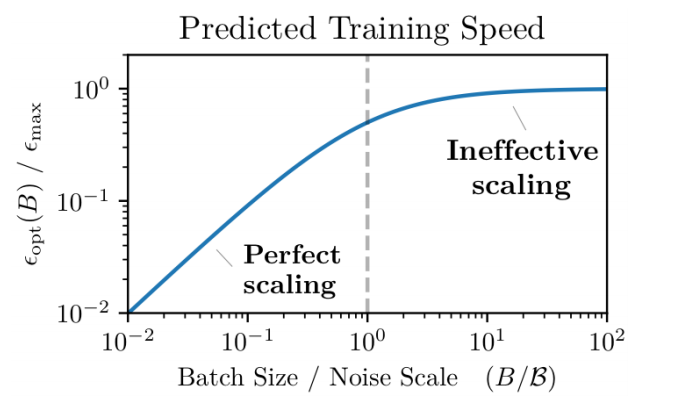
注: 作者在 Appendix D.1 中证明了训练速度和训练样本所满足的一个等式关系 (但是其中的证明我没有推过去).