目录
- Dfs模板
- 原理
- 代码实现
- Bfs模板
- 原理
- 代码实现
- 邻接表
- 拓扑序列
- 原理
- 突破
- 代码实现
- 最短路问题
- Dijkstra
- 代码实现
- bellman_ford算法
- bellamn_ford
- 代码实现
- spfas算法
- 代码实现
- 判断负环
- floid算法
- 代码实现
- Dijkstra
- 最小生成树问题
- Prim算法
- 代码思路
- 代码实现
- Prim算法
Dfs模板

原理
dfs原名叫做深度优先遍历,以上图为例,从1开始1-2-5-,再回溯9-5-2-1再1-3-6-10,再回溯10-6-3,3-7,再回溯7-3-1最后1-4-8这是dfs特殊的走法,不撞南墙不回头的走法
代码实现
定义:dfs是深度优先遍历树中,将每一层搜索完后,回溯再搜下一层
dfs:采用递归来写
const int N=10010;int g[N][N];int st[N];//标记数组,判断是否来过
int n;//传初始参数
void dfs(int u){if(n==u){return ;}for(int i=0;i<=n;i++){if(!st[i]){//修改操作//标记dfs();//还原标记,回溯}}
}int main(){memset(st,-1,sizeof st)
}Bfs模板

原理
bfs原名广度优先遍历,走法如下先从1开始2-3-45-6-7-89-10bfs的走法是一层层遍历,遍历完一层后再遍历下一层
代码实现
定义:bfs是宽度优先遍历树中,先将一层搜索完后,再搜索下一层采用队列存储来实现数组模拟:int q[];//队列int d[]//每个位置的距离int bfs(){//定义对头,队尾int hh=0,tt=0;//初始化队列q[0]=1;//初始化开始点memset(d,-1,sizeof d);d[1]=0;while(hh<=tt){//将对头弹出,并记录储存int t=q[hh++];if(!d[])//d[]==-1说明没有路过,可以记录} return d[];//返回需要到达的终点
}
作用:1.用于求最短路问题
库函数:queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);while (q.size())
{int t = q.front();q.pop();for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (!s[j]){st[j] = true; // 表示点j已经被遍历过q.push(j);}}
}邻接表
定义:一根线,每个线都有一个槽,每个槽上挂一个拉链;
const int N=10010;int e[N],nep[N],idx,head[N];void add(int a,int b){e[idx]=b; ne[idx]=head[a] ;head[a]=idx++;
}邻接表的使用for(int i=h[u];i!=-1;i=ne[i]){//实现操作}
int main(){memset(h,-1,sizeof h);初始化头节点
}
拓扑序列
原理
拓扑序列:有向无环图;采用入度,出度的知识来解决
例子
1---2----3
1-------3
这样就是一个拓扑序| 编号 | 入度 | 出度 |
|---|---|---|
| 1 | 0 | 2 |
| 2 | 1 | 1 |
| 3 | 2 | 1 |
突破

通过入度为零的点作为突破口,不断的来使数进队,使它达到可以满足的条件
代码实现
#include<bits/stdc++.h>using namespace std;const int N=100010;//邻接表的写法
int h[N],e[N],ne[N],idx;
int n,m;
int q[N],d[N];void add(int a,int b){e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}int topsort(){int hh=0,tt=0;while(hh>=tt){int t=q[hh++];//把入度为零的数,入队 for(int i=1;i<=n;i++){q[++tt]=i;}//前面的出去了 for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];d[j]--;//入度减一 if(d[j]==0){q[++tt]=j;} }}cout<<tt<<endl; return tt==n;
}int topsort(){int num=0;queue<int> q;//把入度为零的数,入队 for(int i=1;i<=n;i++){if(d[i]==0){q.push(i);num++;}}while(q.size()){int t=q.front();q.pop();//前面的出去了 for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];d[j]--;//入度减一 if(d[j]==0){q.push(j);num++;} }}cout<<num<<endl; return num==n;
}int main(){cin>>n>>m;memset(h,-1,sizeof h);for(int i=0;i<n;i++){int a,b;cin>>a>>b;add(a,b);d[b]++;}if(topsort()){cout<<"这是拓扑序";}else{cout<<"这不是拓扑序"; } return 0;
} https://www.acwing.com/
最短路问题
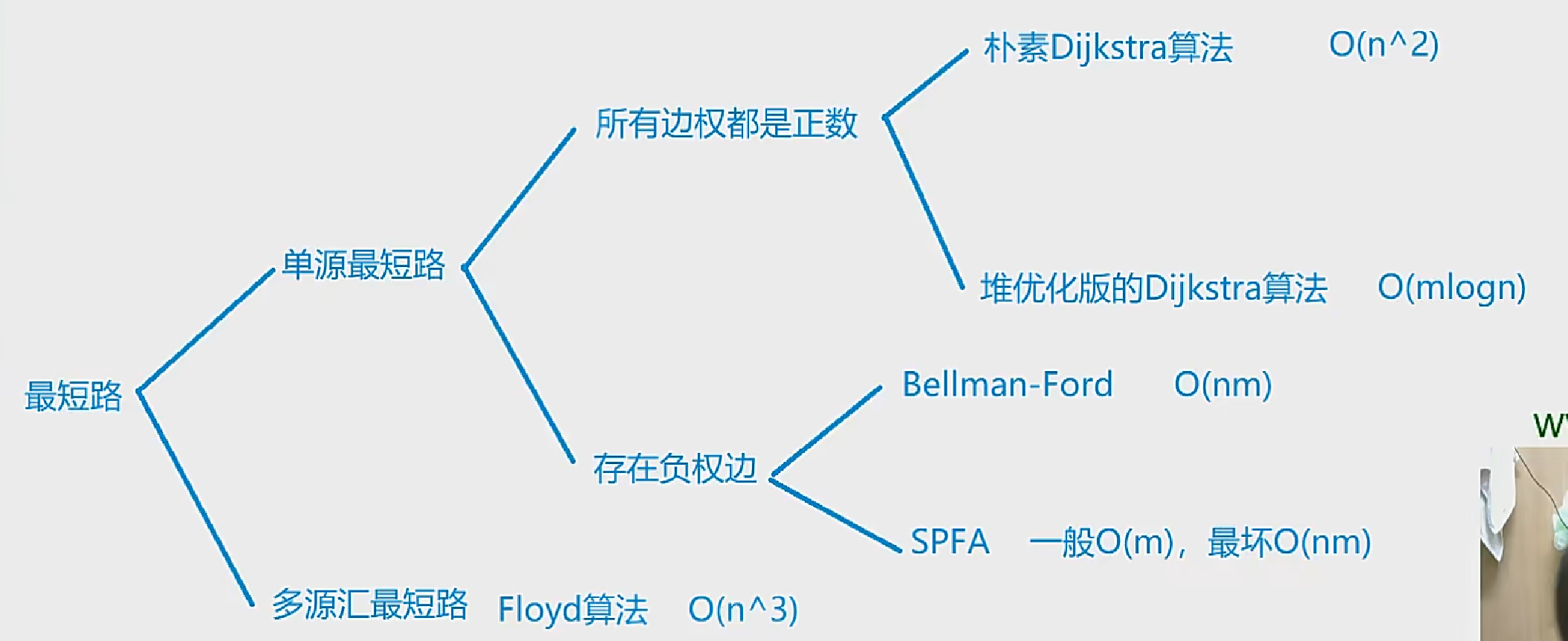
判断是稀疏图还是稠密图
1.边的数量:稀疏图:边的数量远小于可能的最大边数。对于一个有 n 个顶点的无向图,可能的最大边数是
n(n−1)/2(因为每对不同的顶点之间可以有一条边)。如实际的边数 m 远小于 n(n−1)/2,则图被认为是稀疏的稠密图:边的数量接近于或等于可能的最大边数。如果 m 接近于 n(n−1)/2,则图被认为是稠密的。2.边的密度:
可以计算图的密度 ρ,定义为 ρ= 2m/n(n−1)。对于无向图,这个值表示边的实际数量与可能的最大边数之比。
如果 ρ 接近于 0,则图是稀疏的;如果 ρ 接近于 1,则图是稠密的。
Dijkstra
稠密图:
s:当前以确定最短路距离的点
1.dist[1]=0,dist[i]=+∞;
2.for v 1~nt--不在s中的距离最近的点s--t用 更新其它点的距离
代码实现
#include<bits/stdc++.h>using namespace std;//采用邻接矩阵
const int N=510;
int n,m;//n表示点,m表示边
int g[N][N];//邻接矩阵
int dist[N];//最短距离
bool st[N]; //判断是否已经又最短距离int Disjkstr(){memset(dist,0x3f,sizeof dist);//初始化最短距离成无穷dist[1]=0;//起点赋值为一 for(int i=0; i<n ;i++){int t=-1;//变换变量//遍历所有点for(int j=1;j<=n;j++){if(!st[j]&&(t==-1||dist[t]>dist[j])){t=j;//一旦出现这个点没有最短距离,t==-1,不是最短的距离的话,更新t}}st[t]=true;//表示有最短距离for(int j=1;j<=n;j++){dist[j]=min(dist[j],dist[t]+g[t][j]);//用t点更新j点 } }if(dist[n]==0x3f3f3f3f)return -1;//如果到n还是无穷的话说明插入失败return dist[n];//成功,返回最短距离
}int main(){cin>>n>>m;memset(g,0x3f,sizeof g);//初始化邻接矩阵while(m--){int a,b,c;cin>>a>>b>>c;g[a][b]=min(g[a][b],c);//选最短边可以避免重边问题}int t=Disjkstr();cout<<t<<endl;return 0;}
例子
a b c
1 2 1
2 3 4
1 3 3
稀疏图
//堆优化版
#include<bits/stdc++.h>using namespace std;//采用邻接表的方式存储
typedef pair<int ,int> PII;
const int N=510;
int n,m;//n表示点,m表示边
int e[N],w[N],ne[N],idx,h[N];//
int dist[N];//最短距离
bool st[N]; //判断是否已经又最短距离void add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}int Disjkstr(){memset(dist,0x3f,sizeof dist);//初始化最短距离成无穷
priority_queue<PII,vector<PII>,greater<PII>>heap;
heap.push({0,1});//0表示距离,1表示该点,定义起点st[1]=true;while(heap.size()){auto t=heap.top();heap.pop();int ver =t.second,distance=t.first;if(st[ver]) continue;st[j]=true;for(int i=h[ver];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>distance+w[i]){dist[j]=distance+w[i];heap.push({dist[j],j});}}}if(dist[n]==0x3f3f3f3f)return -1;//如果到n还是无穷的话说明插入失败return dist[n];//成功,返回最短距离
}int main(){cin>>n>>m;
memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}int t=Disjkstr();cout<<t<<endl;return 0;}
priority_queue<PII>,vector<PII>
bellman_ford算法
bellamn_ford
1.循环:n次2.循环:所有边a,b,wdist[b]=min(dist[b],dist[a]+w);
dist[b]<=dist[a]+w//三角不等式
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=510,M=100010;int n,m,k;//k为限制的边
int dist[N],backup[N];//定义一个结构体来存储
struct Edge{int a,b,w;
}edge[M];int bellman_ford(){//初始化distmemset(dist,0x3f,sizeof dist);dist[1]=0;for(int i=0;i<k;i++){memcpy(backup,dist,sizeof backup);//在此是bellman_ford的灵魂,避免了自串问题for(int j=0;j<m;j++){int a=edge[j].a,b=edge[j].b,w=edge[j].w;dist[b]=min(dist[b],backup[a]+w);}}if(dist[n]>0x3f3f3f/2)return -1;return dist[n];
}int main(){scanf("%d%d%d",&n,&m,&k);for(int i=0;i<m;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);edge[i]={a,b,c};}int t=bellman_ford();if(t==-1)puts("impossible");printf("%d",t);return 0;
}
spfas算法
它是在dijkstra的基础上,改变只要没有负环,可以用SPFA算法代码实现
//堆优化版
#include<bits/stdc++.h>using namespace std;//采用邻接表的方式存储
typedef pair<int ,int> PII;
const int N=510;
int n,m;//n表示点,m表示边
int e[N],w[N],ne[N],idx,h[N];//
int dist[N];//最短距离
bool st[N]; //判断是否已经又最短距离void add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}int spfa(){memset(dist,0x3f,sizeof dist);dist[1]=0;queue<int> q;q.push(1);st[1]=true;while(q.size()){int t=q.front(); q.pop();st[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];if(!st[j]){q.push(j);st[j]=true;}}}}if(dist[n]==0x3f3f3f3f)return -1;//如果到n还是无穷的话说明插入失败return dist[n];//成功,返回最短距离
}int main(){cin>>n>>m;
memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}int t=spfa();if(t==-1)puts("imposseible");else cout<<t<<endl;return 0;} 判断负环
原理:利用抽屉原理1~n如果出现走了n条边,说明有n+1点
但只有n个点,说明有两个相同的点
//堆优化版
#include<bits/stdc++.h>using namespace std;//采用邻接表的方式存储
typedef pair<int ,int> PII;
const int N=510;
int n,m;//n表示点,m表示边
int e[N],w[N],ne[N],idx,h[N];//
int dist[N];//最短距离
bool st[N]; //判断是否已经又最短距离
int cnt[N];
void add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}int spfa(){//memset(dist,0x3f,sizeof dist);//dist[1]=0;queue<int> q;for(int i=1;i<=n;i++){st[i]=true;q.push(i);}while(q.size()){int t=q.front(); q.pop();st[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=n)return true;if(!st[j]){q.push(j);st[j]=true;}}}}return false;
}int main(){cin>>n>>m;
memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}if(spfa())puts("Yes");else puts("No");return 0;} floid算法
代码实现
#include<bits/stdc++.h>using namespace std;const int N=211 ,INF=1e9;
int d[N][N];
int n,m,Q;void floid(){for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}int main(){scanf("%d%d%d",&n,&m,&Q);//初始化for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j) d[i][j]=0;//为了排除自环问题,重边问题删去即可d[i][j]=INF;}}//添加while(m--){int a,b,w;scanf("%d%d%d",&a,&b,&w);d[a][b]=min(d[a][b],w);}//求最短路floid();while(Q--){int a,b;scanf("%d%d",&a,&b);if(d[a][b]>INF/2)puts("impossible");else printf("%d\n",d[a][b]);}return 0;
}
最小生成树问题
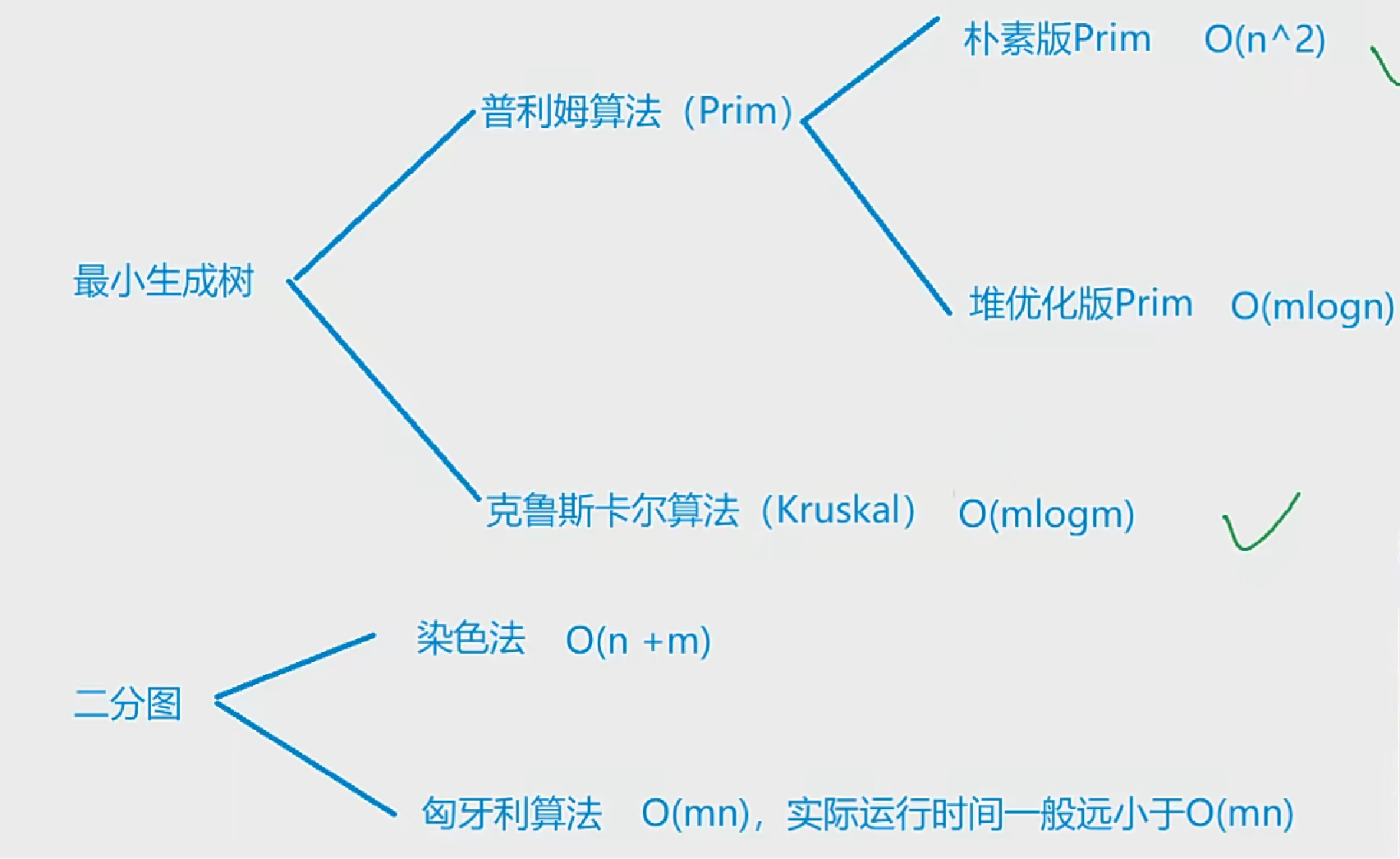
Prim算法
代码思路
这个算法与Dijkstra算法比较相似,都采用了邻接矩阵的方法来实现
第一步:
先初始化距离成无穷
第二步:
遍历最最小值
第三步:
更新res
第四步:
用t更新新的距离
代码实现
#include<bits/stdc++.h>using namespace std;const int N=510,INF=1e9;bool st[N];
int g[N][N],dist[N];
int n,m;//采用邻接矩阵int prim(){//距离初始化成正无穷memset(dist,0x3f,sizeof dist);int res=0;//for(int i=0;i<n;i++){int t=-1;for(int j=1;j<=n;j++) if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;if(i&&dist[t]==INF)return -1;if(i)res+=dist[t]; st[t]=true;//存在后,更新for(int j=1;j<=n;j++) dist[j]=min(dist[j],g[t][j]);//用t来更新新的集合}return res;
}int main(){memset(g,0x3f,sizeof g);//初始化成无穷scanf("%d%d",&n,&m);while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);g[a][b]=g[b][a]=min(g[a][b],c);//无向图}int t=prim();if(t==-1)puts("impossible");else printf("%d\n",t);return 0;
}