习题9.2
点击查看代码
import numpy as np
from scipy.stats import norm, chi2, chisquare
import pylab as pltn = 50; k = 6
a = np.loadtxt('ti9.2.txt').flatten()
mu = a.mean(); s = a.std(ddof=1)
x1 = a.min(); x2 = a.max()
x = np.linspace(14.55, 15.55, k)
bin = np.hstack([x1, x, x2])
h = plt.hist(a, bin); f = h[0]
p1 = norm.cdf(x, mu, s)
p2 = np.hstack([p1[0], np.diff(p1), 1 - p1[-1]])
print('各区间的频数:', f)
print('各区间概率为:', np.round(p2,4))
ex = n * p2
kf1 = chisquare(f, ex, ddof=2)
kf2 = sum(f ** 2 / (n * p2)) - n
ka = chi2.ppf(0.95, k - 2)
print(kf1); print(round(kf2,4))
print('学号:3001')
习题9.3
点击查看代码
import numpy as np
import pylab as plt
import pandas as pd
import statsmodels.api as sm
from scipy.stats import f# 读取数据
a = pd.read_excel('data9.3.xlsx')
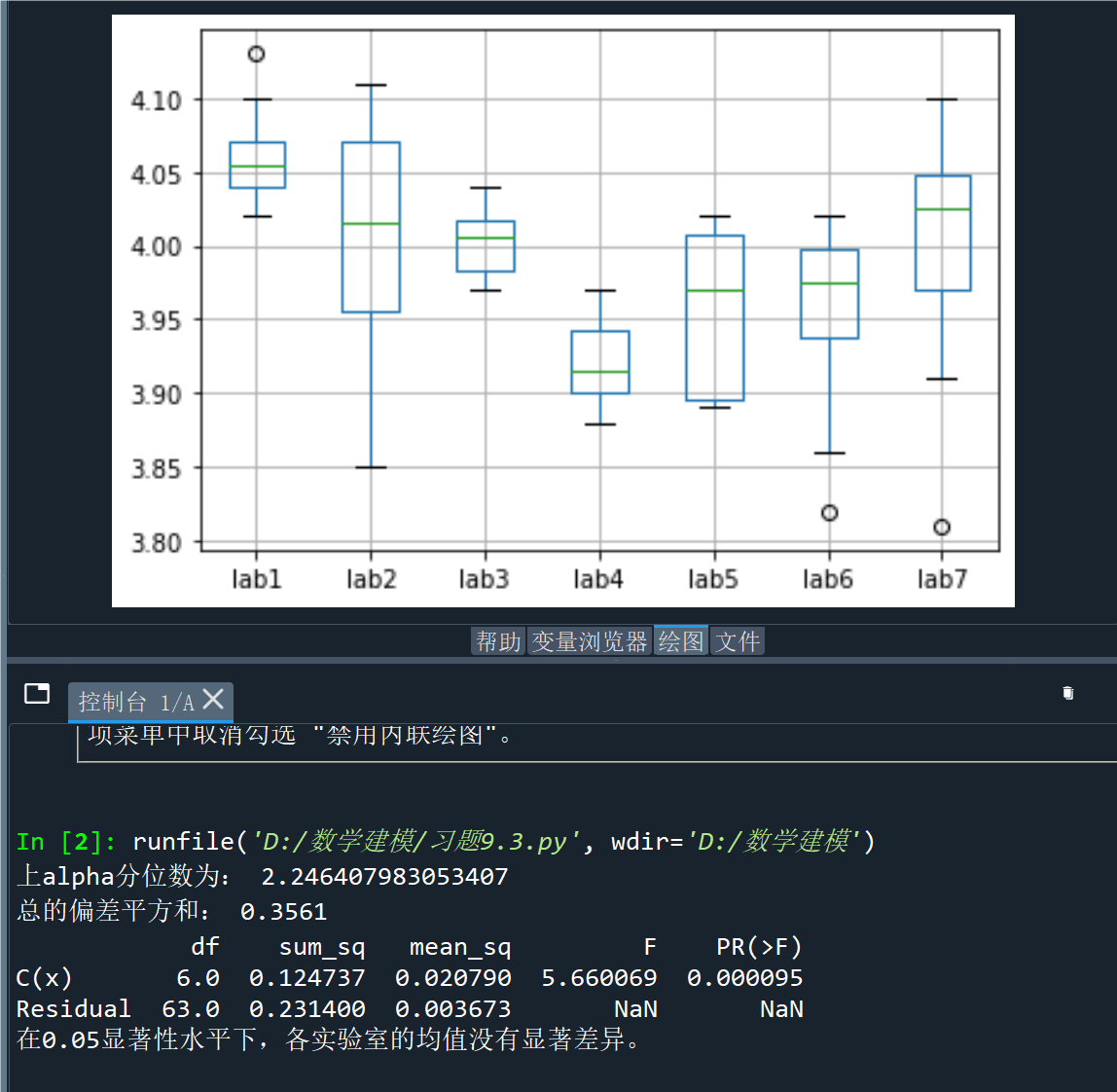
a.boxplot() # 画箱线图
b = a.values.flatten()# 计算上alpha分位数
print('上alpha分位数为:', f.ppf(0.95, 6, 63))# 构造类别变量x
x = np.tile(np.arange(1, 8), (10, 1)).flatten()
d = {'x': x, 'y': b} # x为类别变量# 拟合模型并进行单因素方差分析
model = sm.formula.ols('y ~ C(x)', d).fit()
anova = sm.stats.anova_lm(model) # 进行单因素方差分析# 输出总的偏差平方和
print('总的偏差平方和:', round(sum(anova.sum_sq), 4))
print(anova)# 获取p-value值
p_value = anova['PR(>F)'].iloc[-1]
alpha = 0.05 # 设定显著性水平# 判断是否有显著差异
if p_value < alpha:print("在0.05显著性水平下,各实验室的均值有显著差异。")
else:print("在0.05显著性水平下,各实验室的均值没有显著差异。")plt.show()
print('学号:3001')