浅谈随机化算法

用处

在很多情况下，我们很难想到一道题目的正解，这时候，，我们不应什么都不干，我们可以骗分！

随机化——一种最常用的骗分方式，而且它在大部分情况下只要使用方式正确，就能获得非常高的部分分，有时甚至能骗过整道题

分类

我所知道的随机化算法大致分三种，分别是纯随机、爬山算法与模拟退火算法

纯随机

纯随机看似是纯随机，但是它的作用非常大，只是在一些最优解问题中的表现要略逊于另外两种方法，因为在很多存在解问题中其他两种根本没有必要使用，因为只要找出一组解即可。

纯随机化作用很大，而且写法简单，这里就不再赘述，重点讲其他两种

爬山算法

爬山算法是一种局部择优的方法，采用启发式方法，是对深度优先搜索的一种改进，它利用反馈信息帮助生成解的决策。

直白地讲，就是当目前无法直接到达最优解，但是可以判断两个解哪个更优的时候，根据一些反馈信息生成一个新的可能解。

所以说，爬山算法就是在当前最优的方案下选找下一个更优方案，如果下一次找的的方案没有更优，就会会退回来，类似于一个爬山的过程。

但是，爬山有一个缺点，就是它容易陷入局部最优解，如下图：

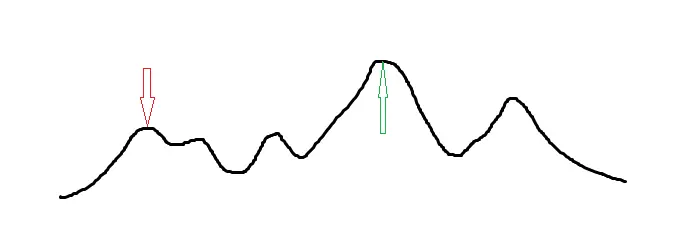
绿色箭头表示全局最优解，而红色的表示爬山可能会陷入的最优解。

为了解决此问题，我们可以多次爬山，取其中最优解。

模拟退火

但是，多次爬山仍然可能出现问题，如下图：

假设红色箭头指向我们现在爬山的到的最优解，灰色箭头指向现在找到的一个可能解，但是灰色箭头要低于红色的，根据爬山，我们现在会放弃灰色部分，但是注意！！！看上面的图，从红色只能爬到蓝色，但是灰色可以爬到当前峰最优解的绿色！！！

为什么会这样？因为爬山只更新更优的解，但是没有考虑如果接受劣解可能会得到更优的结果！！！

因此，我们就有了模拟退火，它的原理类似于下图：(来自oi.wiki)

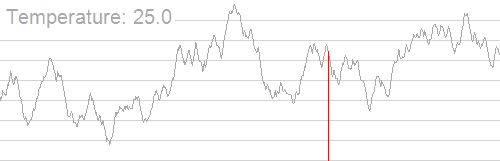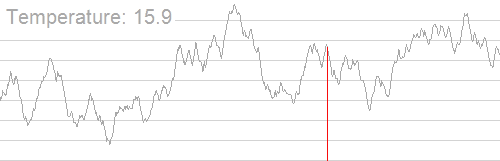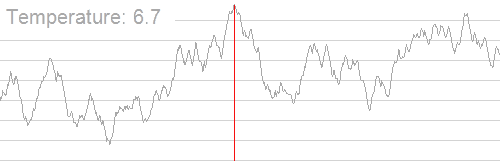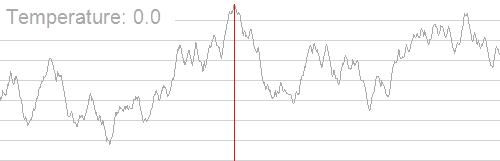
随着温度的降低，跳跃越来越不随机，得到的最优解也越来越稳定。

所以模拟退火的实现就要求我们接受劣解，但是显然，我们并不能接受所有劣解，因为这样会不断更新答案，正确率极低，甚至会不如纯随机。

所以，我们需要设置一个阈值\(ex\)，一般的，我们令\(ex = (1.0\times rand()) / RAND\_MAX\)

若\(exp(-abs(cur - ans) \div T) \geq ex\)，则接受当前劣解，其中\(cur\)表示当前峰前面求得的解，\(ans\)表示本次结果，\(-abs\)是为了保证\(cur - ans > 0\)(也可以看情况而定减的顺序来减小常数)，\(T\)表示当前温度参数，一般来说，温度参数变化幅度越小，深度越深，得到的结果就会越精准。

然而，模拟退火的参数十分重要，要多造几组检查稳定性，实在不行就尝试多参数退火。

一般来说，退火跑得会比爬山慢很多，但是只要参数调的好，正确概率就会大大提升。

完结★,°:.☆(￣▽￣)/$:.°★ 。~~~~~~