[杂题]2024.9~2024.11 杂题总结
题目做多了,不总结,和没做是一样的。
ARC061B
挺好的一道题。观察到三个不好做,我们想能否搞成一个牌堆去取。发现显然是可以的,我们只需要知道一个确定的取出来牌的编号序列,必然可以确定三者的牌堆分别是什么。
所以,问题转换成了:有多少个序列,当 \(A\) 出现 \(n\) 次时,\(B\) 最多出现 \(m\) 次,\(C\) 最多出现 \(k\) 次。我们考虑对此计数。枚举最后一个 \(A\) 的位置 \(i\) ,答案为:
我们考虑 \(O(n)\) 枚举 \(i\),快速计算后面的 \(j\) 的贡献。我们设 \(i'=n-i\),把 \(i'-j\) 的组合数贡献图画出来,是这样的。
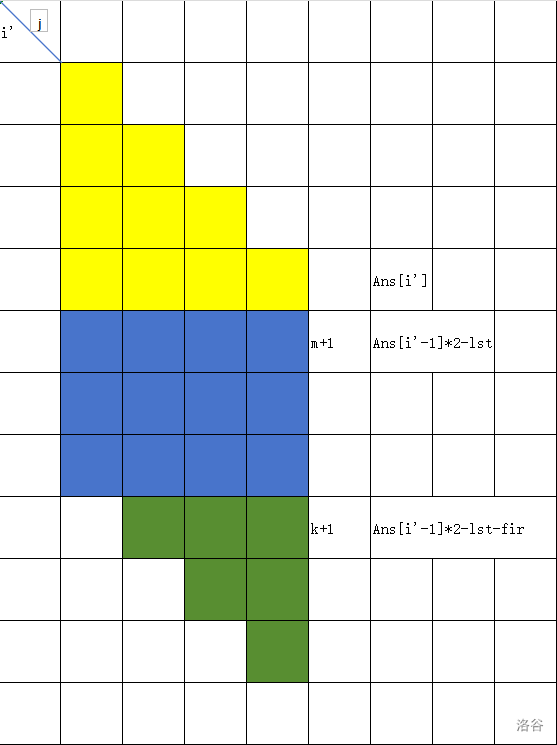
可以发现,在 \(m\) 这个分界点往下,一行的贡献是上一行的贡献 \(\times 2\) 减去上一行最后一个组合数。这是因为:
相当于上面一行给下面一行做贡献,但是最后一个数只做了一次贡献。
所以就可以水过一道黑题了。
AGC050B
发现一个事情:o... $\to $ oooo \(\to\) ...o。
然后考虑区间DP。假设可以有一个分界点,使得 \(mid-l-1\bmod 3=0,r-mid-1\bmod 3=0\),我们可以考虑使用这个区间的前三个点,把它们分别移到 \(l,mid,r\) 的位置。这是一种转移,另一种就是常见的。
ABC346G
小水题,一开始不会做。
考虑枚举右端点 \(r\),统计左端点。一个左端点 \(l\) 合法当且仅当有一种颜色在 \([l,r]\) 中只出现一次。正难则反,考虑颜色给左端点贡献。那么考虑一个左端点合法,当且仅当至少一个颜色给它贡献。这个我们发现颜色贡献的总是一个区间,具体的,对于 \(i\) ,我们先撤销这个点颜色对 \([lst[lst[i]]+1,lst[i]]\) 的贡献,再加上 \([lst[i]+1,i]\) 的贡献。用线段树维护有几个位置为 \(0\) 即可(可以维护区间最小值个数)。
NOI2021轻重边
为数不多的国赛简单题(虽然不看题解我也不会。)
做个转化:每次把 \((u,v)\) 这条链的点赋一个新的颜色,一条边是否为重链的充要条件就是:它连接的两个点是否为同色的。
这个我们显然线段树维护相邻颜色相同的个数,开个三元组 \((fir,lst,sum)\) ,合并的时候判断一下 \(l.lst\) 和 \(r.fir\) 是否同色。查询时,特殊关照一下两条重链的交接,直接拿两个三元组 \(L,R\),维护左边那些重链的合并、右边那些重链的合并。注意一下,由于越往上dfn越小,所以合并时新的重链在前面。我们对最后的 \(L\) 头、尾swap,再和 \(R\) 合并。
然后你要注意懒标记在build()的时候就要清空。
梦熊CPS-S模拟youyou 的序列 II
挺好的一道题,就是写了4.4K,考场上因为T1的sb错误没时间想了。
我们发现:如果这个区间的最大值 \(maxn\) 大于 \(w1\) ,那么youyou必败。令yy能染色的区间为合法区间。否则,我们考虑一个事情:youyou不能一次染完剩下还没染成红色的合法区间,youyou还是必败。
那么我们只需要考虑youyou是否能够一次染完最左的合法区间的左端点到最右的合法区间的右端点。这个我们可以将 \([l,l+c_2-1]\) 看成一个数,在线段树上维护最大值,单点修变成区间查。我们需要做线段树上二分(无非就是找到最左、最右的合法区间),可以这样考虑。找到一个线段树区间被包含于 \([ql,qr]\) (它是最左的or最右的)满足它的最大值大于 \(w_2\)。然后我们发现只需要在这个完整的线段树区间上做一般的线段树上二分就好了。
你还要维护 \(a\) 的区间最大值、\(a\) 的单点加和区间查和,再写一棵线段树和树状数组即可。
梦熊CSP-S模拟youyou 不喜欢夏天
又是挺好的一道题,还是因为时间不足没有仔细想。
我们发现:对于两个 \(0\) 和两个 \(1\) 的情况,对于前者,我们肯定全选;对于后者我们只需要选一个保持联通即可。
再发现:一个 \(0\) 一个 \(1\) ,我们要么全选,要么在保证联通性的情况下选 \(1\)。
于是对于全选的,yy无法操作使得答案更小,设两个 \(1\) 的贡献是 \(2\),两个 \(0\) 的情况为 \(0\) ,其他的是\(-1\)。做最大子段和。
后者,我们写DP,选了几个 \(1\) 就是几的贡献,答案直接减去 \(2m\)。和上者取 \(\max\)。
梦熊CSP-S模拟youyou 的垃圾桶
先说sb错误:lzy下传到左儿子的时候,乘上的贡献是 \(l-mid+1\) 的,而不是 \(mid-l+1\) 的!!!!!!!
发现我们只需要维护一个全局和,然后二分没死的轮数,还有一些贡献,在线段树上二分,记得乘上比较的时候乘上 \(2^c\) 的贡献。写完发现开O2还要跑3s多,最后20min极限写快读快输竟然要1+eps秒,相信评测机波动,不改了!
早知道就听LiuIR的话,背fread板子了……虽然还是以0.89s的成绩AC了。
[JSOI2016] 炸弹攻击1
很唐的模拟退火。注意到范围很大,可能一直走在更劣的路上,所以限制一个范围:最小-R~最大+R。不符合范围的坐标,直接返回-INF。
说句闲话:这道题,我下午写的,晚上换成爬山就过了;找lnw143,看他弄了40min,才知道要有范围限制。
「KDOI-03」还原数据
发现正着做根本做不了,正难则反。考虑反过来做,发现区间加变成区间减,取max操作,如果这个最大值大于区间最小值,那么发现正着做会超出,所以只能是区间最小值。所以初始化使用 \(a'\),你会发现 \(a\) 根本没用,因为题目保证有解,于是维护一个支持区间加&区间最小值的线段树即可。
一定要清lzy,不然像OIer_ljb一样红温。
AtCoder_DP_Contest_U
\(O(n^3)\) 的子集枚举DP典题。一般地,这种题总是让我们分组,我们设 \(f_{i,s}\) 表示考虑完前 \(i\) 个组,不考虑再放元素进去,然后所用的元素集合是 \(s\)。之后就枚举补集的子集。枚举子集如下枚举(比如说我要枚举 \(p\) 的子集):
for(int k=p;k;k=(k-1)&p)
CF773D
学军给的杂题,挺不错的一道题!就是感觉结论不太好证明,但是又很好猜?
首先我们注意到完全图,这启示我们每两个点之间都有边相连,限制相当松。考虑一种情况:由于是路径上最小值之和,大胆猜测关键在于一条权值最小的边。可以让根连这个最小边的一个点,另一个点连菊花。但是可能菊花和根的边的值相当大,导致十分不优。考虑类似一条链连着菊花头和根,就是一个扫帚形状。我们定义扫把是:这个链自上而下除了最后两条边的链。也就是不包括最小边和刚好链接最小边一个端点的那条链。
这个结论不太好猜:扫把的权值自上而下是单调不升的。这是因为:


之后考虑做最短路。发现一件事:假设扫帚有 \(cnt\) 个点,那么答案是 \(dis[i]+(n-cnt-1)\cdot minn\)。不好维护,但是发现 \(cnt\) 刚好等于从 \(i\) 走到权值最小边的一端的边数,我们直接给每条边的边权减去最小值,统计答案的时候直接加就好了。
说一下一个细节:就是发现我们无法判断链接最短边的那条边是否也满足单调性。但不过可以这样做:dis[i]=min(dis[i],w[i][j]*2)。是更大的,也会被它上面的那条边贡献;更小的,后续跑最短路会被贡献的。
记得跑多源多汇Dij!即一开始把所有节点都塞进队列!!!
CF1190B
随机和Cyanwind一起duel的一道题。然而被Cyanwind秒了,我还不会。
我们先考虑一点开局时的特殊情况。
- 出现两个0;
- 出现大于等于两组相等元素;
- 有一组相等元素,还有一个元素是这组相等元素-1,这样无论怎么做,都还是会让先手输。
排序完之后特判。再考虑现在的情况下,最终局面是怎么样的。就是:\(0,1,2,\cdots ,n-1\)。我们统计这里的和,还有开始的 \(\sum a_i\),后者减前者就是两个玩家总的操作次数。判断一下奇偶性即可。
Luogu_P10635
神仙结论题。首先考虑怎么只让一个位置变色。假设这个位置是 \((x,y)\),我让第 \(x\) 行的都操作、第 \(y\) 列的都操作(当然这个位置只操作其中一次),那么有如下事实:
- 对于 \((u,v)\) (其中 \(u\neq x,v\neq y\)),它必然被 \((x,v)\) 和 \((u,y)\) 这两个点的两次操作反色两次,相当于没反色。
- 对于 \((u,y)\) 或者 \((x,v)\) (其中 \(u\neq x,v\neq y\)),注意到 \(n\) 是偶数,那么同一行肯定是被反色偶数次,相当于没反色。
再考虑这样进行为什么是最优的。首先,现在我们可以确定最终局面有 \(2^{n^2}\) 种,操作序列是 \(2^{n^2}\) 中;所以一种操作序列必定对应一个局面;一个局面确定了,那么其操作序列也必定确定了;两者构成双射关系。由此可见,我们把无用操作去掉,这样做必定是最优的。
所以给要变色的格子的行、列分别打+1标记;统计答案时,判断行列标记之和加上是否要变色最终是否是奇数,如果是给答案加一。
Luogu P8037
不错的数据结构,题解都是千篇一律的:开两颗线段树,一棵在单调栈上维护;另一颗维护不能修改的点的答案。但是讲题人的做法非常巧妙。
发现直接做比较困难,不妨考虑钦定最左边是最小值、最右边是最大值。另一种情况序列、询问的 \(l,r\) 反过来即可。
那么考虑转换。设 \(f_i\) 是在 \(i\) 右边第 \(1\) 个 \(a_{f_i}<a_i\) 的位置;设 \(g_i\) 是在 \(i\) 左边第 \(1\) 个 \(a_{g_i}>a_i\) 的位置。\([l,r]\) 合法,等价于 \(r<f_l,l>g_r\)。
在线不会,考虑离线。我们从小到大加入右端点的贡献、尝试区间查一段左端点的答案。考虑辅助数组 \(c,d\),一开始令 \(\forall i,c_i=-\inf,d_i=-\inf\)。
\(d_i\) 表示 \(i\) 作为左端点的时候的最大贡献。当扫到 \(i\) 时,令 \(c_i=-i\);当扫到 \(f_i\) 时,令 \(c_i=-\inf\)。考虑加入新的右端点 \(r\) 的贡献。相当于:\(\forall i\in [g_r+1,r],d_i=\max(d_i,c_i+r)\)。
仔细思考,这是可以用一棵线段树同时维护 \(c,d\) 的。这个方法的巧妙之处在于:通过赋值和扫描线去掉了烦人的二维限制。
CF1801G
字符串好题,所需知识点并不多高级,但是一些套路比较典,是很有必要借鉴的。最关键的莫过于:对于字符串的子串,我们可以考虑处理前缀/后缀而避免处理子串的麻烦。
一开始,让我们拜谢Alex_Wei。
首先,想一想能不能差分。假设 \(f_i\) 是前缀 \(t{[1,i]}\) 所有合法的后缀数量,\(g_i\) 是最长合法后缀所对应的模式串编号,\(h_i\) 是\(f_i\) 的前缀和数组。发现 \(h_i\) 的值就是 \(t[1,i]\) 所有合法子串的数量。
自然想法是:答案就是 \(h_r-h_{l-1}\)。当然这还是太 naive 了,我们没有注意到左端点在 \([1,l)\) 、右端点在 \([l,r]\) 这样的贡献。我们考虑怎么消除这类情况的影响。
假设我们能找出一个最大 \(p\),满足 \(p\in[l,r],p-|s_{g_p}|<l\) ,那么所有右端点 \(r'>p\),它们的合法后缀 \(f_{r'}\) 的左端点都不可能再小于 \(l\) 了。所以一部分贡献是 \(h_r-h_{p}\);再考虑右端点在 \([l,p]\) 的合法子串,那么这一部分贡献就是 \(g_{p}\) 长度为 \([1,p-l+1]\) 的这一后缀的所有合法子串。
对于 \(f,g,h\) 我们直接正向建ACAM然后再ACAM上转移即可;对于第二部分贡献,我们考虑全部倒过来,到着来做ACAM,即可把后缀化成同前面情况的前缀了(相当于 \(h\) 的作用。)具体地,设 \(c_{i,j}\) 表示 \(i\) 这个模式串,长度为 \(j\) 的这个后缀有多少个子串是合法的。
怎么找 \(p\) 呢。考虑线段树上二分。我们可以维护区间的 \(p-|s_{g_p}|\) 的最小值,然后如果一个区间的最小值都要大于我们要求的值,那么这个区间就不合法。能走右边就走右边,不行就走左边。
复杂度是 \(O(\sum |s|+|t|+m\log |t|)\)。比较优秀。注意ACAM的tot从0开始,数组开够!!!
CF196E
好题,挺考验图论转化能力的。首先我们发现,假设我们已经开启了第1个传送门,那么是不是肯定是走最短路到其他传送门。随着传送门的数量变多,我们从哪一个开始走到另一个没开启的选择也会变多。这相当于一棵最小生成树,但是由于我们走到边都是最短路,不难想到这样的朴素暴力:全源最短路跑出两两之间的最短路,把这个作为新的边权,连 \(O(k^2)\) 条边,再跑最小生成树。
显然跑不过去一点。我们考虑这样一个事情:假设有三个点 \(x,y,z\) ,设 \(dis_{u,v}\) 表示 \(u\) 到 \(v\) 的最短路,满足 \(dis_{x,y}+dis_{y,z}=dis_{x,z}\),可以肯定的是:\(x\to z\) 这个新边必然没有用,不会使答案更优。我们如何减少这样边的数量呢?考虑每个点找到其最近的关键点并且设距离为 \(dis_i\) 关键点是 \(d_i\),然后让原图的边变成 \((u,v,w)\to (d_u,d_v,dis_u+dis_v+w)\),就可以发现:我们只考虑两个点分别最近的点,这样完美的避开了上述情况。找最近的关键点使用多源多汇最短路即可。注意双向边开两倍空间。
CF2038D
经典性质+套路题,不过赛时真的搞心态?赛时写了主席树,发现要2G的空间,题目只给了512M,不会扫描线,破防。
不难设出朴素DP:\(f[i][v]\) 表示以 \(i\) 结尾,最后一段是 \(v\) 的方案数。转移显然是 \(f[j][v']\to f[i][v]\),其中需要满足 \(j\le i,v=v'\le\operatorname{OR}_{k=j+1}^{i} a_k\)。
考虑优化。一般这个时候,出题人就会注意到什么性质了。观察题目要求的是或运算,我们可以猜测:\(f[i][v]\) 第二维的不同取值最多有 \(O(\log V)\) 个,其中 \(V\) 是 \(a\) 的值域。而且或起来的结果相同的左端点 \(j\) 一定是一段段区间,所以可以考虑区间进行整体转移。那这样一个点的状态被降到了 \(O(\log V)\) ,\(n\) 个点的状态被降到了 \(O(n\log V)\) 个。
这个时候发现要求 \(j\in [l,r],v'\le v\),才能从 \(f[j][v']\) 转移到 \(f[i][v]\)。我赛时就写了主席树。结果写了2h+发现:空间是错的!!!这启发我们要好好分析空间再实现。
考虑扫描线。我们先对 \(O(n\log V)\) 个DP第二维不同的取值进行离散化。发现是在 \(i\) 这个位置我们才对 \(f[i][v]\) 进行被动转移,这样就优化不了。于是考虑相对应的主动转移配合扫描线。比如说我们要求 \(j\in [l,r],v'\le v\) 这样的 \(f[j][v']\) 转移到 \(f[i][v]\) ,不妨开vecotr数组,在 \(l\) 这个地方加上给 \(f[i][v]\) 贡献的负标记,在 \(r+1\) 这个地方加上给 \(f[i][v]\) 贡献的正标记。第二维我们直接树状数组维护即可。然后到一个下标 \(p\) ,先处理它的标记,再让它的DP值贡献到树状数组。
找 \(O(\log V)\) 个区间是 naive 的。首先考虑ST表维护区间or值,然后二分这些区间的端点。
复杂度是:\(O(n\log n\log V)\)。
AGC019C
VP的时候不会特判,然后就在想怎么大力特判,被最后一个样例搞自闭了……
最开始的想法肯定是做一个LIS,就是往上、往左走,经过的喷泉越多越好。因为每经过一个喷泉,我都可以让曼哈顿距离少 \(20-5\pi\)。这个时候看到最后一个样例,我们发现可能会有转 \(180\) 度的情况。我们考虑在什么情况下会出现。
我也不知道其他人怎么发现的:当经过的喷泉数等于两点之间(包括两点所在的)行或列数时。由于题目保证了每行每列最多一个喷泉,所以如果方案是刚才那种,我们必然会在最上面的行/最右边的列再绕 \(\dfrac{1}{4}\) 圆周。
之后是一些细节:首先保证起始点在终点左下角。这个可以通过交换起始点、终点以及给 \(y\) 做一个 \(\inf-y\) 做到。然后要注意:横坐标小于起始点或者纵坐标小于起始点,我们不应该进行DP。
ABC314G
我做这个题的时候比较人机,做了有2h左右。中间有40多min是在思考代码怎么写。
首先我们发现可以考虑将其转成判定性问题:前缀 \(r\) 在用 \(p\) 护身符的情况下是否合法。又发现答案是单调不降的,那么 \(r,p\) 直接双指针扫。现在思考怎么判定。我们肯定把护身符用在前缀 \(r\) 中,攻击值之和前 \(p\) 个大的,我们还要维护这前 \(p\) 大的攻击值之和。这是个前 \(k\) 大的问题,使用对顶multiset维护即可。
ABC345E
如果你没注意到 \(5s\) 时限、如果想到wqs二分、如果你想最外层枚举删了几个,你就输麻了。
这种DP设二维状态,一定要把删了几个在放里面枚举,否则考虑不了连续删的情况。
设出DP状态 \(f[i][j]\) 表示钦定 \(i\) 保留,并且前 \(i\) 个删了 \(j\) 个。那么转移就是:考虑上一个保留的位置 \(p\) 以及它所删的位置个数 \(q\),将 \([p+1,i-1]\) 删光,就可以 \(f[i][j]=\max(f[p][q])+a[i]\)。这样是 \(O(nk^2)\),因为你最多一下删 \(k\) 个。
考虑优化。人类智慧地,我们观察 \(i,j,p,q\) 四个变量之间的关系。发现只有当 \(i-p-1=j-q\to i-j-1=p-q\) 时,我们才能转移。于是考虑维护前面所有满足状态 \(i-j=k\) 的最大值、次大值以及它们的颜色,要求最大值、次大值颜色不同。做完一个 \(i\) 才用它的DP值更新 \(i-j\) 的最大值、次大值。
ABC308G
一道被队爷秒了、我不会的G题。
首先你可以线段树分治+01Tire。但是我不会01Trie,就不会维护所有点对异或值的最大值;也不会线段树分治。那么队爷让我找性质。
假设 \(x\le y\le z\) 那么 \(\min(x\oplus y,y\oplus z)\le x\oplus z\)。给出证明:我们从二进制高到低位考虑三者异或值。
- 某一位上 \(x,y,z\) 都为 \(0\) 或 \(1\),那么这是无关紧要的。
- 某一位上 \(x\) 为 \(0\),\(y\) 为 \(0\),\(z\) 为 \(1\):显然,这一位上的 \(x\oplus y<x\oplus z\),因为前者结果为 \(0\) 后者为 \(1\)。
- 某一位上 \(x\) 为 \(0\) ,\(y\) 为 \(1\),\(z\) 为 \(1\):显然,这一位上的 \(y\oplus z<x\oplus z\),理由同上。
所以我们暴力是 \(O(n^2)\) 的,现在排序后只用看相邻两个,是 \(O(n)\) 的。考虑数据结构优化,开两个 multiset 维护相邻的异或值、有哪些 \(x\) 即可。
ABC343G
想了2h,因为没看出来是TSP,被抬走了。
这个题看到 \(n\le 20,|S|\le 2\times 10^5,5s\)。你就觉得很不对劲,是不是要出事。发现想到贪心真的出事了。这个问题是TSP问题,根本不能贪。
想想怎么转化,一开始被包含肯定先处理掉,它们对答案无影响。首先我们可以把一个串接在另一个串的后面,省了一点字符,这个可以字符串哈希+\(O(n)\) 暴力判断即可。我们想:假设省了 \(x\) 个字符,那么其实我们从字符串 \(i\) 的结尾花了 \(len_j-x\) 的代价走到了 \(j\) 的结尾。我们走后是走遍所有字符串的结尾,在哪一个结尾不知道。
考虑建图。连 \((i,j,len_j-x)\) 这样的有向边。相当于我们随便从一个点开始旅行,要求旅行完所有城市,求方案中代价最小。这是经典 NP-hard 问题 TSP 问题,你是不可能在多项式时间复杂度内解决的,这就是这道题开 \(5s\) 的理由。最后考虑状压即可。
ABC343F
之前ABC的时候没做出来,被现在的自己一眼秒了。
经典的,维护最大值、次大值以及它们的数量。注意一下怎么合并。直接线段树即可。
CF1844G
神·Ad-hoc题目。但是CHD5min速通????????
首先你什么都不会,但是你会 \(dis(u,v)=d_u+d_v-2d_{lca}\)。其中 \(d_u\) 表示从根到 \(u\) 的距离。所以你现在钦定 \(i\) 为根。然后你惊奇的发现:\(2d_{lca}\),这启示我们往二进制上靠。考虑我们是否能求出所有 \(d_i\) 在 \(\bmod 2\) 意义下的值。那么就会发现:\(d_1=0,d_i\equiv a_i-d_{i-1}(b\bmod 2)\) 因为 \(2\) 的系数在 \(\bmod 2\) 下结果为 \(0\)。
之后你回了 \(\bmod 2\) ,想想怎么 \(\bmod 4\)。首先考虑结论 \(x\bmod 4=(2x)\bmod 8\),也就是 \(2(x\bmod 2^{k})=(2x) \bmod 2^{k+1}\),考虑二进制下的模就是截取后面的值,左边相当于先截少一位再左移回去,右边相当于先左移一位再截,除了左移,涉及到都是前 \(k\) 个位,所以是一样的。那么就是 \(d_i\equiv 2(d_{lca}\bmod 2) +a_i-d_{i-1}\) 。推广到一般情况:\(d_i\equiv 2(d_{lca}\bmod 2^{k-1})+a_i-d_{i-1}(\bmod 2^k)\)。这就可以递推了。后面判断一下是否是 \(-1\) 即可。
CF620E
凑数用的题目。非常水。观察到只有 60 种颜色,直接每个线段树节点开个 bitset<62> 即可。
CF1847D
一开始看错题了,发现十分不可做。后来被队爷提醒才发现。
首先我们发现肯定是把 \(1\) 填到前面的的区间是更优的。然后再发现:如果当前区间和前面区间有交,那么由于前面的操作都是按最优的来,不可能再被改了,所以有交部分对于这个区间是不重要的。我们把区间内重要的部分看做一种颜色。那我们要对没有覆盖颜色的地方附上现在的颜色,自然想到珂朵莉树。所以一个点只有一种颜色。
再想想,发现不仅是填到前面的区间,还要是填到前面的区间前面的位置。所以我们还要知道它是这个颜色的第几个数,这个是容易的。
之后思考答案是怎么来的。那么我们已经知道 \(1\) 要填哪些位置了,那么答案就是最大 \(1\) 的数量减去这些这些位置已经有 \(1\) 的位置数量。现在问题成了维护后者。显然前面一部分颜色是都可以填满 \(1\) 的,给颜色长度做个前缀和加上 lower_bound() 就可以轻松知道是多少个。其实问题成了统计 \(pos\le v\) 的 \(a_{pos}=1\) 的数量,显然可以树状数组。
调了一个早上的原因:发配给这个颜色的第几个出错了,用错计数器。
ABC356F
我用 2-set 大法写了3.4K,跑了100ms+,你也试一下吧!
首先是对题目性质的发掘。建图太突兀了,这一定需要转化:排序后,一个子图的点一定是一段区间,而且这个区间任意两个数的差的绝对值不超过 \(K\)。这个非常关键。
那我们要做的事情就是尽可能向左、向右扩展这个区间。思考我们已经维护了若干个区间了,而且这些区间是不交的,加入一个数字会发生什么:有可能会让它左右的区间连起来。删除反之。这就不难想到珂朵莉树。所以我们开一个 set<int> 维护一个数的前后继,set<pair<long long,long long> > 维护这些区间。
发现题目有一个不起眼的性质:每个数最多出现一次。对于询问,我们可以知道它所在的区间的 \(l,r\) ,现在问题变成了:在当前集合内,有多少个数满足 \(\in [l,r]\)。直接离散化+树状数组即可。
ABC341G
首先先做转换:\([l,r]\) 的平均数为 \(\dfrac{s_r-s_{l-1}}{r-(l-1)}\),那么把 \((i,s_i)\) 试做平面上的点,\(l\) 最优的 \(r\) 一定是求出凸包后与 \((l+1,s_{l+1})\) 相连的节点。那么直接 Andrew 倒着跑即可。说一下我竟然不会的凸包:首先爽关键字排序,左到右求下凸壳,右到左求上凸壳;每次判断栈顶和倒数第二个元素 \(S_1,S_2\) ,如果满足 \(\overrightarrow{S2S1} \times \overrightarrow{S1X}<0\),那么弹栈。叉积公式为 \(x_1y_2-x_2y_1\)。
ABC328G
首先你得猜结论:最多执行一次 \(1\) 操作。那么考虑怎么做。相当于我们要钦定一些在 \(b\) 中的位置已经被选过,现在再钦定一些位置对于 \(a\) 中的值。看到 \(n\) 很小,考虑状压。设 \(f_s\) 表示 \(b\) 中被选的位置在 \(s\) 二进制那一位中为 \(1\)。然后考虑转移。显然我们可以一个区间集体转移,使得只多一次 \(c\)。
复杂度分析:
假设一个区间为 \(k\),那么除了 \(k\) 个连续的位置,其他任选,还要考虑起始点,所以是:
ABC319G
典典典。只要你做过某场ARC一道可以用线段树模拟DIJ以优化 \(O(n^2)\) 的题、XYD上一道出在模拟赛可以线段树模拟Prim求最小生成树的题,这道题也是可以线段树模拟DIJ的。做法就是不能走的边看做断点,直接两个断点之间区间修改即可。所以不要忘记线段树模拟Prim、DIj和其他算法。
ABC307G
首先可以确定较大值的数量和较小值的数量。那么发现:无论怎么操作,\(\sum {a_i}\) 是不会变的,对于每个前缀来说。看到 \(n\le 5000\),考虑 \(O(n^2)\) 的DP。设 \(f[i][j]\) 表示做完了前 \(i\) 个数,有 \(j\) 个是较大值。我们可以通过 \(s_{i+1}\) 推出 \(a_i\) 变成较大值或较小值的代价,转移为:\(f_{i,j}\to f_{i+1,j+1},f_{i,j}\to f_{i+1,j}\)。水题咋不会?
ABC141F
首先进行一些观察。如果二进制下某一位上出现 \(1\) 的次数为奇数,无论我们怎么分配,总会产生 \(2^j\) 的贡献。所以现在我们考虑完奇数次二进制位的贡献后,只考虑出现偶次的二进制位。注意到:这些数全部异或起来,必定为 \(0\);所以假设 \(a,b\) 是一种方案,必定有 \(a\oplus b=0\to a=b\)。我们在保证 \(a\) 最大的情况下,自然保证 \(b\) 也最大。相当于求一个集合的子集最大异或和,直接线性基即可。
ABC283G
典+板。直接线性基即可。但是我们发现我们的线性基代码是这样写的:
for(int i=0;i<=m;++i)if(p[i])d[++tot]=p[i];
LL qry(LL k)
{LL res=0;for(int i=tot;i>=1;i--)if(k&(1ll<<i))res^=d[i];return res;
}
所以我们发现:二进制下最低那一位其实是没有用的,但是我们访问的 \(k\) 这一位是有用的。所以问 \(k\) 小是qry((k-1)<<1)。如果没 \(0\) 不用减一。
ARC092B
考虑拆位。我们考虑对于一个 \(a_i\) ,每一位上同时处理 \(n\) 个 \(b_j\)。考虑这一位上怎么样是 \(1\),假设 \(a_i\) 这一位是 \(1\),那么要么 \(b_j\) 这一位是 \(0\) 并且不能进位。进位可以 \(\bmod 2^{p+1}\) 看一下是否 \(\le 2^{p}-(a_i\bmod 2^{p})-1\)。其他情况差不多,就是考虑一下进位。然后每一个 \(\bmod 2^{p}\) 开数组。相当于统计多少个 \(b_j\) 在 \(\bmod 2^p\) 下值域在 \([l,r]\) 的数量。lower_bound 和 upper_bound 即可。
ABC150F
首先断环成链。那么考虑转化:\(a'_i\oplus x=b_i\to a'_i\oplus b_i=x\),所以对应的每一个 \(a'_i\oplus b_i\) 它们的值都应该相等。考虑拆位,那么一位上,要么所有 \(a_i\) 都等于 \(b_i\),要么全都不一样。这个考虑一个 \(n\) 位的二进制数,那么直接哈希即可。
LG P10463 Interval GCD
首先观察到区间做不好做,所以考虑能不能转化成单点做。我们考虑 \(\gcd\) 的性质:\(\gcd(a,b)=\gcd(b,a-b)\)。那么联系到差分,假设我们设差分数组 \(b_i=a_{i+1}-a_i\),那么考虑一下 \(\gcd(a_l,\cdots ,a_r)\) 是怎么样的。注意到:\(\gcd(a_l,b_l,b_{l+1},\cdots ,b_{r-1})=\gcd(a_l,a_{l+1}-a_l,a_{l+2}-a_{l+1},a_{l+3}-a_{l+2},\cdots a_{r}-a_{r-1})=\gcd(\gcd(a_l,a_{l+1}-a_l),\cdots,a_{r}-a_{r-1})=\gcd{a_l,a_{l+1},\cdots a_{r}-a_{r-1}}\)。
所以开两颗,一棵维护单点的值、支持区间修改,一棵维护差分的值& \(\gcd\) ,支持区间修改。
CF223B
首先我们考虑一下怎么让判断一个位置合法:假设对应关系是 \(s_i\to t_j\),那么 \(t_{j+1\to m}\) 要在 \(s[i+1,n]\) 一一对应,\(t_{1,j-1}\) 要在 \(s_{1,i-1}\) 一一对应。而且我们发现一组合法的对应关系是不交的。这个就成了:在一段前缀/后缀,选最后面/最前面合法的,这个可以开26个树状数组解决。之后注意没办法找到一个子序列是合法的情况。
NOIP2012TGD2T3
这个题有点复杂。我们发现:一个点越往上越优,考虑贪心。那么我们考虑一下到底该怎么样往上。直接做太困难,没有任何限制,于是可以二分答案进行一个限制,使得更好做。
这个时候往上的点分为两类:
- 不能到根节点,已经尽力的。
- 可以到根节点,有余力的。
先让尽力的点进行封锁,剩下肯定还有一些点不合法。我们考虑有余力的去到那些子树还不全部合法的、以深度为2的节点的子树。发现:如果一个点(深度为2)的余力,要小于它到根节点的距离,不如直接让它呆着不动。因为它也去不到根节点距离比它大的深度为2的点,让更大的去显然不劣。还剩下的点就贪心匹配。
ABC295G
自己做出来的,开心!
首先发现一开始给出的是有向边的树,而且加入的点总是满足祖孙关系。然后就想到了强联通分量,首先加入的边像DFS生成树的返祖边,因为一个SCC内的点总是走不出去的。
那我们现在考虑一件事,假设加入边是 \((u,v)\):
- \((u,v)\) 隶属同一个SCC,无事发生。
- 否则,会使得 \(u\to v\) 这条往上找祖先的所有经历过的点、它们所在的SCC,全部变成一个,变成 \(v\) 的SCC。
这个时候就分析出来:要求一些集合变成一个,问一个点是哪个集合,考虑并查集。发现暴力往上跳是很慢的,所以考虑一个一个SCC的跳。具体地:i=fah[Find(i)]。如果遇见了已经是 \(v\) 中的SCC的点,就 break。可证明,这样最多是 \(O(n)\) 的,因为在一个集合内的我们统一处理了。
P8600
套路题,还是不会……杂题出过类似的。
题意相当于:\(\sum[\max_{i\in[l,r]}a_i-\min_{i\in[l,r]}=r-l]\)。考虑转化:\(\max-\min +l=r\)。发现经典不等式:\(\max-\min+l\ge r\)。所以假设我们能维护右边式子区间的最小者以及它们的个数,就好办了。用线段树是简单的。
每次加入一个 \(a_r\) 都会使区间最小值/最大值发生改变。考虑单调栈,因为单调栈中存的 \(l\) 相当于把区间最小值/最大值的取值分成若干个段,我们直接对这些段暴力做区间修改。这样的复杂度是对的,因为一个点最多被弹一次,弹的那次才会做区间修改,所以是 \(O(n\log n)\) 的。