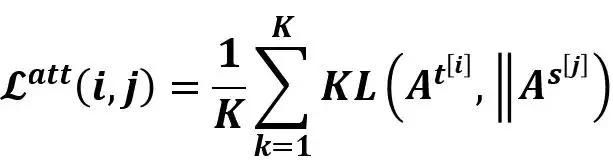前言
过于水的一场。
A Counting Passes
题面
给出一个长度为 \(n\) 的序列 \(a\),求出 \(a\) 之中大于等于 \(l\) 的数个个数。
\(1\le n\le 100,1\le a_i\le 1000,1\le l\le 1000\)。
制約
- 入力は全て整数
- $ 1\ \le\ N\ \le\ 100 $
- $ 1\ \le\ L\ \le\ 1000 $
- $ 0\ \le\ A_i\ \le\ 1000 $
思路
简单暴力。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,l,cnt;
int a[1001];
signed main()
{//freopen(".in","r",stdin);//freopen(".out","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>l;for(int i=1;i<=n;i++){cin>>a[i];if(a[i]>=l) cnt++;}cout<<cnt<<"\n";return 0;
}
B Minimize Abs 1
题面
有一个长为 \(N\) 的数列 \(A\) 和两个整数 \(L,R\)。对于每个 \(A_{i}\),你需要选出一个数 \(X_{i}\),满足如下条件:
- \(L\le X_{i}\le R\)
- 对于所有整数 \(L\le Y\le R\),\(|X_{i}-A_{i}|\le|Y-A_i|\)
制約
- $ 1\leq\ N\leq\ 2\times\ 10^5 $
- $ 1\leq\ L\leq\ R\ \leq\ 10^9 $
- $ 1\leq\ A_i\leq\ 10^9 $
- 入力は全て整数
思路
只需要根据范围求出 \(|Y-A_i|\) 的最小值,找一个 \(X_{i}\) 使得 \(|X_{i}-A_{i}|= min{|Y-A_i|}\) 即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,a[200005],l,r;
signed main()
{//freopen(".in","r",stdin);//freopen(".out","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>l>>r;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){if(l<=a[i]&&a[i]<=r) cout<<a[i]<<" ";else if(a[i]<l){cout<<l<<" ";}else{cout<<r<<" ";}}return 0;
}
C Minimize Abs 2
题面
给你一个整数 \(D\) ,找到对于非负整数 \(x,y\) 的 \(|x^2+y^2-D|\) 的最小值
制約
- $ 1\leq\ D\ \leq\ 2\times\ 10^{12} $
- 入力は全て整数
思路
只需枚举 \(x\),\(y\) 取 \([\sqrt{D-x^2},\sqrt{D-x^2}+1]\),再计算最小值即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int d;
int minn=2e9;
signed main()
{//freopen(".in","r",stdin);//freopen(".out","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>d;for(int i=1;i<=1e6;i++){int x=i;int y=sqrt(abs(x*x-d));int y2=y+1;minn=min(minn,abs(x*x+y*y-d));minn=min(minn,abs(x*x+y2*y2-d));}cout<<minn<<"\n";return 0;
}
D Counting Ls
题面
现有一个 \(N\) 行 \(N\) 列的字符数组,满足对于每个 \(1 \le i \le N,1 \le j \le N\) 都有 $ S_{i,j} \in {o,x} $
请问在该数组里有多少个满足以下条件的三方格组:
-
三个格子内都是 \(o\)
-
三个方格互不相同
-
恰好有两个方格在同一行
-
恰好有两个方格在同一列
思路
先预处理每一行 o 的数量 \(h_{i}\) 和每一列 o 的数量 \(l_{i}\)。
对于每一个位置,如果它是 o,那它的贡献就是 \((h_{i}-1)\times(l_{i}-1)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,ans;
char a[2001][2001];
int h[2001],l[2001];
int hz,lz;
signed main()
{//freopen(".in","r",stdin);//freopen(".out","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];if(a[i][j]=='o') h[i]++;}hz+=h[i];}for(int j=1;j<=n;j++){for(int i=1;i<=n;i++){if(a[i][j]=='o') l[j]++;}lz+=l[j];}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(a[i][j]=='o') ans+=(h[i]-1)*(l[j]-1);}}cout<<ans<<"\n";return 0;
}
E Mex and Update
题面
给定一个序列,支持单点修改,每次修改后输出全局 \(\operatorname{mex}\)。
一个序列的 \(\operatorname{mex}\) 定义为,序列中最小的没有出现过的非负整数。
制約
- 入力は全て整数
- $ 1\ \le\ N,Q\ \le\ 2\ \times\ 10^5 $
- $ 0\ \le\ A_i\ \le\ 10^9 $
- $ 1\ \le\ i_k\ \le\ N $
- $ 0\ \le\ x_k\ \le\ 10^9 $
思路
首先易证明一个长度为 \(n\) 的序列的 \(\operatorname{mex}\) 最大为 \(n\)。
那我们可以用一个 set 存没出现过的数,一个 map 记录每个数字在序列里出现的次数。
对于每次修改,我们将 \(mp_{a_{x}}\) 减 \(1\),将 \(mp_{y}\) 加 \(1\)。
如果 \(mp_{a_{x}}\) 减到 \(0\),把这个数字加到 set。
如果 \(mp_{y}\) 为 \(1\),则从 set 里删除这个数。
最后输出 set 的第一个数字就行了。
// LUOGU_RID: 191957479
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,q;
int a[200005];
set<int> s;
map<int,int> mp;
signed main()
{//freopen(".in","r",stdin);//freopen(".out","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>q;for(int i=0;i<=n+1;i++) s.insert(i);for(int i=1;i<=n;i++){cin>>a[i];if(a[i]>n) a[i]=n+1;if(s.count(a[i]))s.erase(a[i]);mp[a[i]]++;}while(q--){int x,y;cin>>x>>y;if(y>n) y=n+1;mp[a[x]]--;mp[y]++;if(mp[y]==1) s.erase(y);if(mp[a[x]]==0) s.insert(a[x]);cout<<*s.begin()<<"\n";a[x]=y;}return 0;
}
F Minimize Bounding Square
题面
给定平面内 \(n\) 个点,你可以把这 \(n\) 个点一共在坐标上移动 \(k\) 次。移动可以是横着或者竖着走 \(1\) 单位长度。移动结束后会有一个最小的正方形把所有点都框起来。最小化这个正方形的边长。
制約
- 入力は全て整数
- $ 1\ \le\ N\ \le\ 2\ \times\ 10^5 $
- $ 0\ \le\ K\ \le\ 4\ \times\ 10^{14} $
- $ 0\ \le\ X_i,Y_i\ \le\ 10^9 $
思路
二分答案,对于一个边长 \(x\),只要使得每一对的 \(x_i\) 和 \(y_i\) 经过 \(k\) 次操作后绝对值在 \(x\) 以内即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,k;
int x[200005],y[200005];
bool check(int len){int cnt=0;for(int i=1;i<=(n>>1);i++)cnt+=max(0LL,x[n-i+1]-x[i]-len)+max(0LL,y[n-i+1]-y[i]-len);return cnt<=k;
}
signed main()
{//freopen(".in","r",stdin);//freopen(".out","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>k;for(int i=1;i<=n;i++){cin>>x[i]>>y[i];}sort(x+1,x+n+1);sort(y+1,y+n+1);int l=0,r=1e16,ans=0;while(l<=r){int mid=(l+r)>>1;if(check(mid)){ans=mid;r=mid-1;}else l=mid+1;}cout<<ans<<"\n";return 0;
}