ABC382

news/2025/2/13 11:04:35/文章来源:https://www.cnblogs.com/zuoqingyuan114/p/18579035

上午 NOIP 太憋屈了，我要切水恢复一下信心（

~~希望 cy 别看见~~

aaa

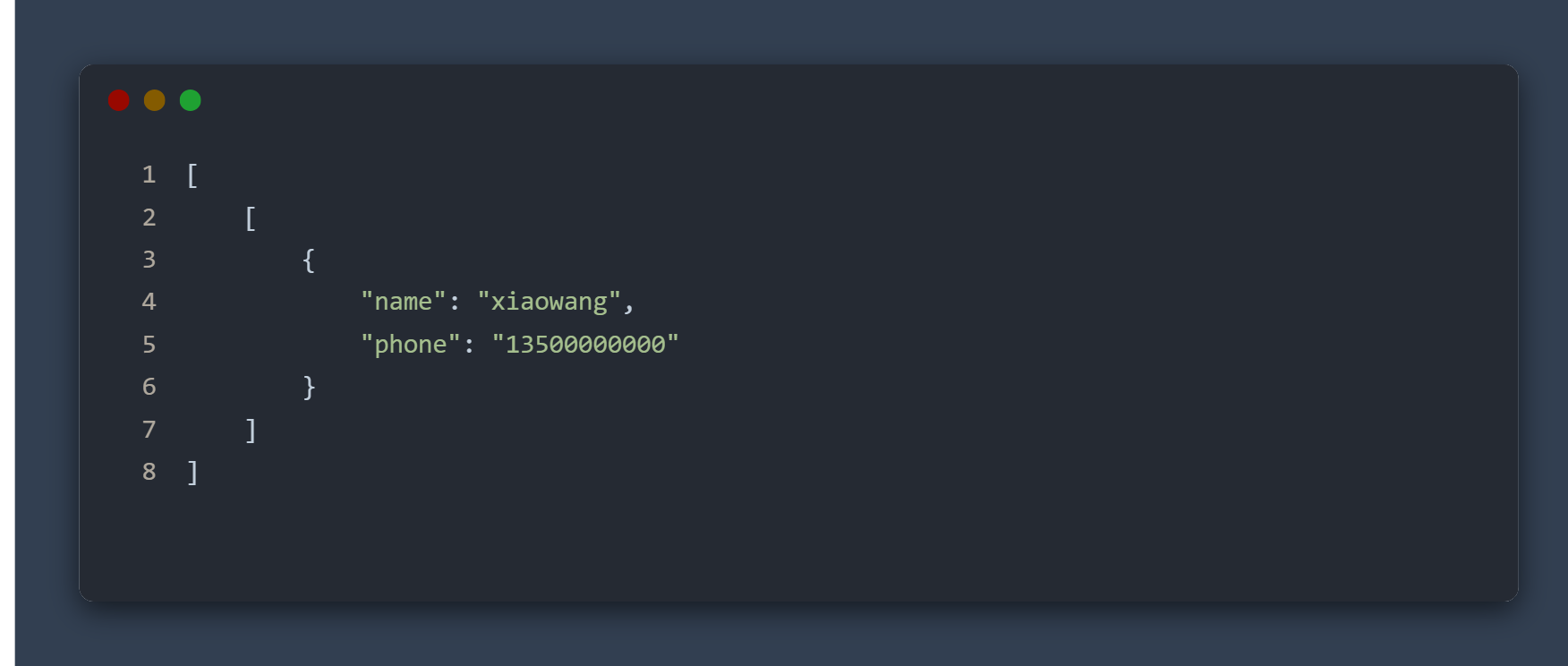
在题目限制中，已经确定 \(S\) 中 @ 字符的个数多于 \(D\)。所以我们直接数 . 的个数加上 \(D\) 就可以。

时间复杂度 \(O(n)\)。

点击查看代码

#include <iostream>
#include <cstdio>
using namespace std;
const int N=105;
char s[N];
int d,n,ans;
int main(){scanf("%d %d",&n,&d);scanf("%s",s+1);for(int i=1;i<=n;i++)ans+=(s[i]=='.');ans+=d;printf("%d\n",ans);return 0;
}

跟上面那题一样，这次我们直接维护一个指针从 \(n\) 扫到 \(1\)，把最先遇到的前 \(D\) 个 @ 变为 .，最后输出即可。

时间复杂度 \(O(n)\)。

点击查看代码

#include <iostream>
#include <cstdio>
using namespace std;
const int N=105;
char s[N];
int d,n,ans;
int main(){scanf("%d %d",&n,&d);scanf("%s",s+1);int it=n;for(int i=1;i<=d;i++){while(it&&s[it]!='@')it--;s[it]='.';}for(int i=1;i<=n;i++){printf("%c",s[i]);}return 0;
}

C - Kaiten Sushi

如果存在 \(i,j\)，满足 \(i<j\) 且 \(A_i<A_j\)，那么 \(j\) 是一定吃不到寿司的，因为 \(j\) 可以吃的寿司都会被 \(i\) 提前偷吃。

所以我们去除所有的 \(j\)，则剩下的 \(i\) 一定满足 \(A_i\) 单调递减，直接二分查找第一个人即可。

时间复杂度 \(O(n\log n)\)。

点击查看代码

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N=2e5+10;
int n,m,t;
int a[N],b[N];
int lower(int x){int l=1,r=t;while(l<r){int mid=(l+r)>>1;if(a[mid]<=x)r=mid;else l=mid+1;}return l;
}
int main(){scanf("%d %d",&n,&m);for(int i=1,x;i<=n;i++){scanf("%d",&x);if(!t||a[t]>x)a[++t]=x,b[t]=i;}for(int i=1,x;i<=m;i++){scanf("%d",&x);if(x<a[t])printf("-1\n");else printf("%d\n",b[lower(x)]);}return 0;
}

因为偷懒想用 lower_bound 花费了不少时间。

D - Keep Distance

入机搜索题。

枚举 \(A_1\) 的取值，然后搜索剩下的数。

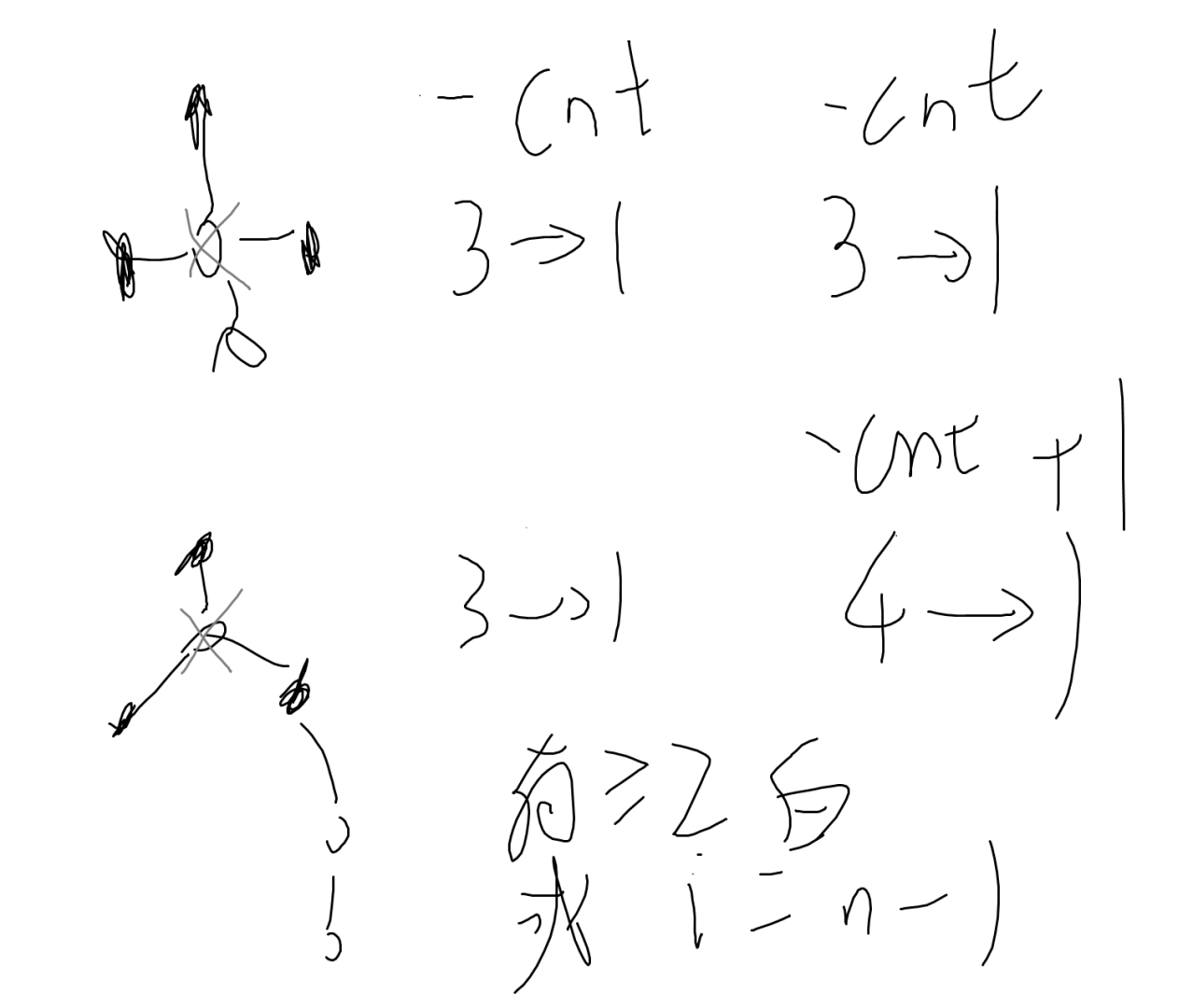
纯爆搜会超时，我们只需加上一个小优化，假设当前要填第 \(A_i\) 位，因为接下来 \(i\) 每增加 \(1\)，\(A_i\) 就会增加 \(10\)，所以此时的 \(A_i\) 必须满足 \(A_{i-1}+(n-i+1)\times 10\le M\)，否则就没有搜索的必要了。

可以搜两次，第一次统计方案数，第二次输出方案。

点击查看代码

#include <iostream>
#include <cstdio>
using namespace std;
int n,m,a[13],ans;
inline void print(){for(int i=1;i<=n;i++)printf("%d ",a[i]);printf("\n");
}
inline void dfs(int x){if(x>n)print();else{for(int i=10;a[x-1]+i<=m;i++){if((n-x+1)*10+a[x-1]>m)return;a[x]=a[x-1]+i;dfs(x+1);a[x]=0;}}return;
}
inline void DFS(int x){if(x>n){ans++;}else{for(int i=10;a[x-1]+i<=m;i++){if((n-x+1)*10+a[x-1]>m)return;a[x]=a[x-1]+i;DFS(x+1);a[x]=0;}}return;
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++){a[1]=i;DFS(2);}printf("%d\n",ans);for(int i=1;i<=m;i++){a[1]=i;dfs(2);}return 0;
}

这道题最开始写时数组开小，后面调好后提交没有发现 TLE，比赛还有 \(10\min\) 的是否发现没过，差点忘了。

E - Expansion Packs

期望题，不会。

F - Falling Bars

读题读了好长时间。。。话说为什么我的 Atcoder Better 不能用了？

首先没一个条都可以表示成一条纵坐标为 \(x_i\)，两个端点横坐标分别是 \([l_i,r_i]\) 的线段。

我们考虑按照初始时的纵坐标从大到小的顺序考虑它最后会移到第几排。

假设现在枚举到了第 \(i\) 条线段，我们枚举它下面的线段 \(j\)，用 \(\min\{R_j\}-1\to R_i\)。
这样就得到了 \(O(n^2)\) 的算法。

事实上，可以直接用线段树维护 \([1,w]\) 上的区域，每计算出 \(R_i\)，就用其更新 \([l_i,r_i]\) 上的区域，计算 \(R_i\) 时，就快速查询 \([l_i,r_i]\) 上的最小值。我的做法是区间取 \(\min\) 区间查 \(\min\) 线段树。但也有用区间赋值区间查 \(\min\) 的更为简单的做法（其实差不多）。

时间复杂度 \(O(n\log n)\)。

点击查看代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#define ls (p<<1)
#define rs (p<<1|1)
using namespace std;
const int N=2e5+10,inf=1e9+10;
struct sgt{int mn[N<<2],tag[N<<2];bool used[N<<2];void push_up(int p){mn[p]=min(mn[ls],mn[rs]);}void push_down(int p){if(!used[p])return;mn[ls]=min(mn[ls],tag[p]);mn[rs]=min(mn[rs],tag[p]);tag[ls]=min(tag[ls],tag[p]);tag[rs]=min(tag[rs],tag[p]);used[ls]=used[rs]=1;used[p]=0,tag[p]=inf;}void build(int p,int l,int r){mn[p]=tag[p]=inf;used[p]=0;if(l==r)return;int mid=(l+r)>>1;build(ls,l,mid),build(rs,mid+1,r);return;}void change(int p,int l,int r,int L,int R,int v){if(L<=l&&r<=R){mn[p]=min(mn[p],v);tag[p]=min(tag[p],v);used[p]=1;}else{int mid=(l+r)>>1;push_down(p);if(L<=mid)change(ls,l,mid,L,R,v);if(R>mid)change(rs,mid+1,r,L,R,v);push_up(p);}return;}int ask(int p,int l,int r,int L,int R){if(L<=l&&r<=R)return mn[p];int mid=(l+r)>>1,cnt=inf;push_down(p);if(L<=mid)cnt=min(cnt,ask(ls,l,mid,L,R));if(R>mid)cnt=min(cnt,ask(rs,mid+1,r,L,R));push_up(p);return cnt;}
}tr;
struct node{int x,l,r,id;
}a[N];
bool cmp(node a,node b){return a.x>b.x;
}
int h,w,n,ans[N];
int main(){scanf("%d %d %d",&h,&w,&n);for(int i=1,r,c,L;i<=n;i++){scanf("%d %d %d",&r,&c,&L);a[i]=node{r,c,c+L-1,i};}sort(a+1,a+1+n,cmp);tr.build(1,1,w);for(int i=1;i<=n;i++){ans[a[i].id]=min(tr.ask(1,1,w,a[i].l,a[i].r)-1,h);tr.change(1,1,w,a[i].l,a[i].r,ans[a[i].id]);}for(int i=1;i<=n;i++)printf("%d\n",ans[i]);return 0;
}