实验二:逻辑回归算法实现与测试
一、实验目的
深入理解对数几率回归(即逻辑回归的)的算法原理,能够使用 Python 语言实现对数
几率回归的训练与测试,并且使用五折交叉验证算法进行模型训练与评估。
二、实验内容
(1)从 scikit-learn 库中加载 iris 数据集,使用留出法留出 1/3 的样本作为测试集(注
意同分布取样);
(2)使用训练集训练对数几率回归(逻辑回归)分类算法;
(3)使用五折交叉验证对模型性能(准确度、精度、召回率和 F1 值)进行评估和选
择;
(4)使用测试集,测试模型的性能,对测试结果进行分析,完成实验报告中实验二的
部分。
三、算法步骤、代码、及结果
1. 算法伪代码
开始
导入必要的库
导入 pandas
导入 PCA 从 sklearn.decomposition
导入 matplotlib.pyplot
导入 train_test_split 从 sklearn.model_selection
导入 DecisionTreeClassifier 从 sklearn.tree
导入 precision_score, recall_score, f1_score 从 sklearn.metrics
定义数据文件路径
读取 CSV 文件到数据框 df
打印数据量
打印数据框的前几行
打印空值数量统计
打印数据框的描述性统计
删除数据框中的 'Id' 列
定义标签索引,将物种名称映射到数字
将 'Species' 列中的物种名称转换为数字标签
提取特征和标签
特征 X = df 中的四个特征列
标签 y = df 中的 'Species' 列
进行主成分分析 (PCA)
创建 PCA 对象,设置主成分数量为 2
拟合并转换特征数据 X
绘制 PCA 结果的散点图
使用特征数据的前两个主成分绘制散点图
根据标签 y 设置点的颜色
显示图形
将数据集拆分为训练集和测试集
使用 stratify 参数确保每个类的比例相同
设置随机种子以确保可重复性
打印训练集和测试集的数据量
创建决策树分类器
设置标准为 'gini'
设置分割策略为 'best'
设置最大深度为 5
设置类别权重为 'balanced'
设置随机种子以确保可重复性
训练决策树分类器
使用测试集进行预测
打印精确度
打印召回率
打印 F1 分数
结束
2. 算法主要代码
完整源代码\调用库方法(函数参数说明)
'''
Created on 2024年11月23日
@author: 席酒
'''
import sklearn
from sklearn import datasets
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Perceptron
# 加载iris数据集
iris = datasets.load_iris()
# 只提取后两类特征
X = iris.data[:, [2, 3]]
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 特征缩放
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
# 训练感知机模型
ppn = Perceptron(max_iter=40, eta0=0.1, random_state=0)
ppn.fit(X_train_std, y_train)
# 计算训练集预测结果
y_train_pred = ppn.predict(X_train_std)
# 计算训练集的准确率、精度、召回率和F1分数
train_accuracy = accuracy_score(y_train, y_train_pred)
train_precision = precision_score(y_train, y_train_pred, average='weighted')
train_recall = recall_score(y_train, y_train_pred, average='weighted')
train_f1 = f1_score(y_train, y_train_pred, average='weighted')
# 输出训练结果
print("Training Accuracy:", train_accuracy)
print("Training Precision:", train_precision)
print("Training Recall:", train_recall)
print("Training F1 Score:", train_f1)
# 计算测试集预测结果
y_pred = ppn.predict(X_test_std)
# 计算测试集的准确率、精度、召回率和F1分数
test_accuracy = accuracy_score(y_test, y_pred)
test_precision = precision_score(y_test, y_pred, average='weighted')
test_recall = recall_score(y_test, y_pred, average='weighted')
test_f1 = f1_score(y_test, y_pred, average='weighted')
# 输出测试结果
print("Testing Accuracy:", test_accuracy)
print("Testing Precision:", test_precision)
print("Testing Recall:", test_recall)
print("Testing F1 Score:", test_f1)
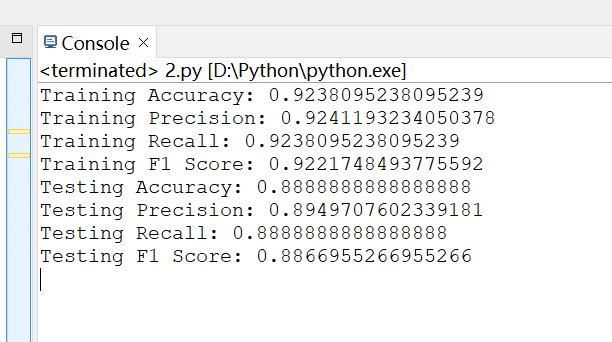
3. 训练结果截图(包括:准确率、精度(查准率)、召回率(查全率)、F1)
四、实验结果分析
1. 测试结果截图(包括:准确率、精度(查准率)、召回率(查全率)、F1)
2. 对比分析
训练集的准确率为 92.38%,而测试集的准确率为 88.89%。模型在训练集上表现良好,但在测试集上的表现略有下降。训练集的精度为 92.41%,测试集的精度为 89.50%。测试集的精度略低于训练集,模型在测试集上预测的正类样本中,实际为正类的比例有所下降。训练集的召回率为 92.38%,测试集的召回率为 88.89%。测试集的召回率与训练集相同,模型在测试集上能够识别出大部分的正类样本,但仍然有一定的下降。训练集的 F1 分数为 92.22%,测试集的 F1 分数为 88.67%。测试集的 F1 分数低于训练集,进一步表明模型在测试集上的整体表现不如训练集。