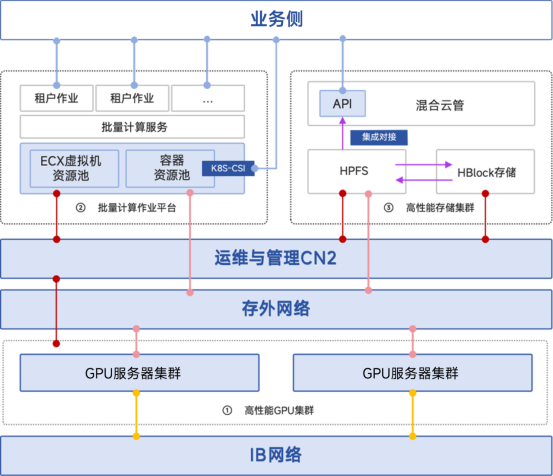
有一个数列 \(a_1\sim a_n\),如果存在 \(l\sim r\) 使得 \(2\mid r-l+1\) 而且 \(a_{l+x}=a_{l+\frac{r-l+1}{2}+x}(0\le x\le \frac{r-l+1}{2})\)(即一个字符串连续出现两次),则 \(a\) 是平凡的。求问一个数列是不是平凡的。
首先如果有相邻相同的,一定是平凡的。
而且,一定第一位是相同的。按照第一位分段,每一段压缩成一个 hash 值,就转换成了更小规模的子问题,变成一个数后停止分裂。那么我们每层有 \(\mathcal{O}(n)\) 个数,因为尽量保证没有相邻相同,所以一层中一个段的上层段长度至少是他的 \(2\) 倍,所以一共有 \(\mathcal{O}(\log n)\) 层,时间复杂度 \(\mathcal{O}(n\log n)\)。
如果用 map 记录的话,时间复杂度 \(\mathcal{O}(n\log^2 n)\)。