幂零矩阵与幂等矩阵

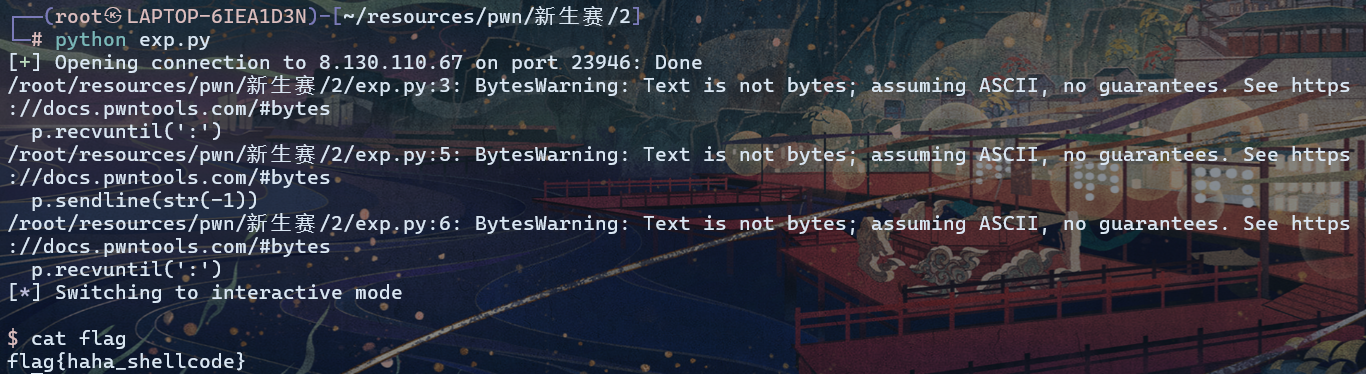
一道线代题目：练习如何使用Latex表示矩阵

将n元二次型( f(x) = X'AX )化为一次因式的乘积，其中
[
A =
\begin{pmatrix}
1 & 2 & 3 & \cdots & n\
2 & 3 & 4 & \cdots & n\
3 & 4 & 5 &\cdots & n\
\vdots & \vdots & \vdots & \quad & \vdots \
n & n+1 & n+2 & \cdots & 2n-1
\end{pmatrix}
]

解答：注意到$ A = (i+j -1)_{n \times n} = BC$，其中
[
B =
\begin{pmatrix}
1 & 1 \
2 & 1 \
\vdots & \vdots \
n & 1
\end{pmatrix}
,\quad
C =
\begin{pmatrix}
1 & 1 & \cdots & 1 \
0 & 1 & \cdots & n-1
\end{pmatrix}
]

因此，

\[f(X) = X'BCX \]

幂等矩阵

参考\href{https://mp.weixin.qq.com/s/AwH7uZPmWR2tk6wE5K-j3A}{一类重要的矩阵——幂等矩阵}

方阵 \(A\)满足 \(A^2=A\) , 则称 \(A\) 为幂等矩阵, 首先我们回顾如下性质: n 级矩阵 A 为幂等矩阵的充要条件是 \(r(A)+r(E-A)=n\).

幂等矩阵一定可以对角化，且幂等矩阵的秩等于迹

幂零矩阵

参考\href{https://mp.weixin.qq.com/s/ICw_nGdg_U9d8FDTtxD0Jw}{其实幂零矩阵是高等代数最核心的东西}

幂零矩阵是矩阵论极为重要的知识点, 这是因为任何方阵都可以相似于一个若尔当形矩阵, 而每一个若尔当块都是 \(aE + J\) 的形式, \textbf{这里 \(J\) 表示对角线元素为零的若尔当块, 它是最重要的幂零矩阵}.

也就是说: 掌握了矩阵 \(J\) 的性质, 结合相似, 我们可以得到所有方阵的性质.

这其中包括计算 \(A^n\), 或者 \(f(A)\), 矩阵秩的各种性质, 最小多项式, 初等因子, 不变因子, 哈密顿-凯莱定理以及著名的不变子空间的直和分解问题(分水岭)等等.

首先, 要充分了解 \(J\) 的运算性质, 这可以通过基本矩阵的性质得到