最小生成树问题模板

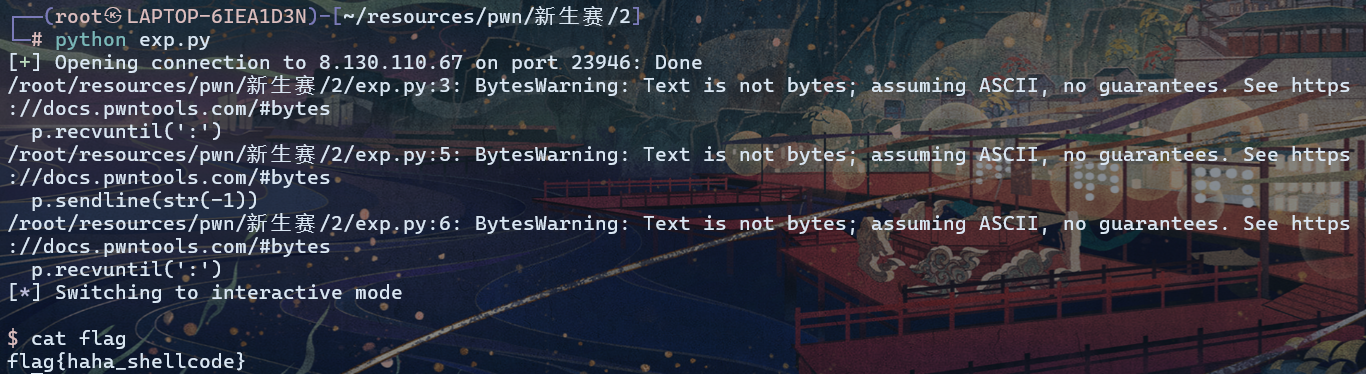
图有最小生成树的充要条件：图是可达的

常见表述：从某节点出发可到达其余节点

#include<bits/stdc++.h>
using namespace std;struct edge
{int a,b,w;bool operator<(edge &other){return w<other.w;}
}e[10001];
int n,m;int p[10001];int find(int x)
{if(p[x]!=x)p[x]=find(p[x]);return p[x];
}
int main()
{cin>>n>>m;for(int i=0;i<m;i++){cin>>e[i].a>>e[i].b>>e[i].w;p[i]=i;}for(int i=1;i<=n;i++)p[i]=i;sort(e,e+m);for(int i=0;i<m;i++){int a=e[i].a;int b=e[i].b;a=find(a);b=find(b);if(a!=b){p[a]=b;if(find(1)==find(n)){cout<<e[i].w<<endl;break;}}}
}

注意点：

1.定义的是<,>根据编译器不同可能报错
2.find函数递归进行路径压缩，将所有节点挂载到根节点上。
3.p[a]=b将一棵树的根挂载到另一棵树上。