比赛链接:https://codeforces.com/contest/2042
这场爆了,卡C题了,QWQ.卡题得跳一跳!!!
A.Greedy Monocarp
题面:
有 \(n\) 个箱子,第 \(i\) 个箱子最初包含 \(a_i\) 枚硬币。对于每个箱子,你可以选择任意非负数(0或更大)的硬币添加到该箱子中,有一个约束条件:所有箱子中的硬币总数必须变成 至少 \(k\)。
在你向箱子中添加硬币后,贪婪的 Monocarp 来了,他想要这些硬币。他会一个接一个地拿走箱子,由于他很贪婪,他总是会选择硬币最多的箱子。当 Monocarp 拿走的箱子中的硬币总数 至少为 \(k\) 时,他将停止。
你希望 Monocarp 拿走尽可能少的硬币,因此你需要以这样的方式向箱子中添加硬币:当 Monocarp 停止拿走箱子时,他将拥有 恰好 \(k\) 枚硬币。计算你必须添加的最小硬币数。
输入:
有 \(t\) 个测试用例,每个测试用例包含两行:
第一行包含两个整数 \(n\) 和 \(k\) (\(1 \le n \le 50\); \(1 \le k \le 10^7\));
第二行包含 \(n\) 个整数 \(a_1, a_2, \dots, a_n\) (\(1 \le a_i \le k\))。
对于每个测试用例,计算需要添加的最小硬币数,使得 Monocarp 拿走的箱子中的硬币总数恰好为 \(k\)。
输出:
对于每个测试用例,打印一个整数 —— 你需要添加的最小硬币数,以便当 Monocarp 停止拿箱子时,他恰好拥有 \(k\) 枚硬币。可以证明,在问题的约束条件下,总是可能实现的。
样例:
4
5 4
4 1 2 3 2
5 10
4 1 2 3 2
2 10
1 1
3 8
3 3 3
————————
0
1
8
2
思路:发现\(a_i<=k\),所以顺着题意,从大到小拿,如果sum最后要溢出,break然后答案为k-sum,如果没溢出最后答案还是k-sum
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
//#include<bits/stdc++.h>
#include <unordered_map>
#define ll long long
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
//const ll p=rnd()%mod;
ll ksm(ll x, ll y)
{ll ans = 1;while (y){if (y & 1){ans = ans % mod * (x % mod) % mod;}x = x % mod * (x % mod) % mod;y >>= 1;}return ans % mod % mod;
}
ll gcd(ll x, ll y)
{if (y == 0)return x;elsereturn gcd(y, x % y);
}
void fio()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
}
ll a[250000];
int main()
{fio();ll t;cin>>t;while(t--){ll n,m;cin>>n>>m;for(ll i=1;i<=n;i++)cin>>a[i];sort(a+1,a+1+n);ll sum=0;ll ans=0;for(ll i=n;i>=1;i--){if(sum+a[i]<=m)sum+=a[i];else {ans=m-sum;break;}}if(ans==0&&sum<=m)ans=m-sum;cout<<ans<<endl;}return 0;
}
B.Game with Colored Marbles
题面:
Alice 和 Bob 玩一个游戏。有 \(n\) 个弹珠,第 \(i\) 个弹珠的颜色是 \(c_i\)。玩家轮流进行游戏;Alice 先开始,然后是 Bob,接着是 Alice,然后是 Bob,以此类推。
在他们的回合中,玩家 必须 从剩下的弹珠中拿走 一个 并将其从游戏中移除。如果没有弹珠剩下(所有的 \(n\) 个弹珠都被拿走了),游戏结束。
游戏结束时,Alice 的得分计算如下:
她为每个颜色 \(x\) 获得 \(1\) 分,只要她至少拿走了一个该颜色的弹珠;
此外,如果她拿走了所有颜色 \(x\) 的弹珠,她还会为每个颜色 \(x\) 额外获得 \(1\) 分(当然,只有游戏中出现的颜色才会被考虑)。
例如,假设有 \(5\) 个弹珠,它们的颜色是 \([1, 3, 1, 3, 4]\),游戏进行如下:Alice 拿走第 \(1\) 个弹珠,然后 Bob 拿走第 \(3\) 个弹珠,然后 Alice 拿走第 \(5\) 个弹珠,然后 Bob 拿走第 \(2\) 个弹珠,最后 Alice 拿走第 \(4\) 个弹珠。那么,Alice 获得 \(4\) 分:\(3\) 分是因为她至少有一个颜色为 \(1\)、\(3\) 和 \(4\) 的弹珠,以及 \(1\) 分是因为她拿走了所有颜色为 \(4\) 的弹珠。注意,这种策略并不一定对两个玩家都是最优的。
Alice 想要在游戏结束时最大化她的得分。Bob 想要最小化它。两个玩家都以最优的方式进行游戏(即 Alice 选择一个策略,允许她获得尽可能多的分数,而 Bob 选择一个策略,最小化 Alice 可以获得的分数)。
计算游戏结束时 Alice 的得分。
输入:
第一行包含一个整数 \(t\) (\(1 \le t \le 1000\)) —— 测试用例的数量。
每个测试用例由两行组成:
第一行包含一个整数 \(n\) (\(1 \le n \le 1000\)) —— 弹珠的数量;
第二行包含 \(n\) 个整数 \(c_1, c_2, \dots, c_n\) (\(1 \le c_i \le n\)) —— 弹珠的颜色。
额外的输入约束:所有测试用例中 \(n\) 的总和不超过 \(1000\)。
输出:
对于每个测试用例,打印一个整数 —— 假设两个玩家都以最优策略进行游戏,Alice 在游戏结束时的得分。
样例:
3
5
1 3 1 3 4
3
1 2 3
4
4 4 4 4
————————
4
4
1
思路:首先对于Alice,她优先拿只有一个的数是最好的,对于Bob也是同理,不妨计这类数的个数为cnt,然后对于存在个数大于等于2的其他数,显然不论Alice先后手,她都一定能有一个,不妨即为cn,所以最后答案为(cnt+1)/2*2+cn.这里直接用了优先队列写
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
//#include<bits/stdc++.h>
#include <unordered_map>
#define ll long long
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
//const ll p=rnd()%mod;
ll ksm(ll x, ll y)
{ll ans = 1;while (y){if (y & 1){ans = ans % mod * (x % mod) % mod;}x = x % mod * (x % mod) % mod;y >>= 1;}return ans % mod % mod;
}
ll gcd(ll x, ll y)
{if (y == 0)return x;elsereturn gcd(y, x % y);
}
void fio()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
}
ll a[250000];
int main()
{fio();ll t;cin>>t;while(t--){ll n;cin>>n; map<ll,ll>q;set<ll>f;for(ll i=1;i<=n;i++){ll x;cin>>x;q[x]++;f.insert(x);}priority_queue<pair<ll,ll>,vector<pair<ll,ll>>,greater<pair<ll,ll>>>op;for(auto j:f){op.push({q[j],j});}map<ll,ll>c;ll j=0;ll ans=0;while(!op.empty()){if(j==0){if(op.top().first==1){ans+=2;j=1;}else if(op.top().first%2==0){j=0;ans++;}else {j=1;ans++;}op.pop();}else {if(op.top().first==1){j=0;}else if(op.top().first%2==0){j=1;ans++;}else {j=0;ans++;}op.pop();}}cout<<ans<<endl;}return 0;
}
C.Competitive Fishing
题面:
Alice 和 Bob 参加了一个钓鱼比赛!总共钓到了 \(n\) 条鱼,编号从 \(1\) 到 \(n\)(鱼越大,编号越大)。这些鱼中有些是 Alice 钓到的,有些是 Bob 钓到的。
他们的表现将根据以下方式评估。首先,选择一个整数 \(m\),并将所有鱼分成 \(m\) 个 非空 组。第一组应该包含一些(至少一条)最小的鱼,第二组应该包含一些(至少一条)接下来最小的鱼,以此类推。每条鱼应该恰好属于一个组,每个组应该是鱼的连续子段。注意,这些组是按照确切的顺序编号的;例如,第二组的鱼不能比第一组的鱼小,因为第一组包含最小的鱼。
然后,将根据组索引为每条鱼分配一个值:第一组的每条鱼获得等于 \(0\) 的值,第二组的每条鱼获得等于 \(1\) 的值,以此类推。因此,第 \(i\) 组的每条鱼获得等于 \((i-1)\) 的值。
每个参赛者的分数仅仅是参赛者钓到的所有鱼的总价值。
你希望 Bob 的分数至少超过 Alice 的分数 \(k\) 分。你必须将鱼分成的最小组数(\(m\))是多少?如果不可能,你应该报告这一点。
输入:
第一行包含一个整数 \(t\) (\(1 \le t \le 10^4\)) —— 测试用例的数量。
每个测试用例的第一行包含两个整数 \(n\) 和 \(k\) (\(2 \le n \le 2 \cdot 10^5\); \(1 \le k \le 10^9\))。
每个测试用例的第二行包含一个字符串,由恰好 \(n\) 个字符组成。第 \(i\) 个字符是 '0'(表示第 \(i\) 条鱼被 Alice 钓到)或 '1'(表示第 \(i\) 条鱼被 Bob 钓到)。
额外的输入约束:所有测试用例中 \(n\) 的总和不超过 \(2 \cdot 10^5\)。
输出:
对于每个测试用例,打印一个整数 —— 你必须将鱼分成的组数的最小值;如果不可能,则打印 -1。
样例:
7
4 1
1001
4 1
1010
4 1
0110
4 2
0110
6 3
001110
10 20
1111111111
5 11
11111
——————————
2
-1
2
-1
3
4
-1
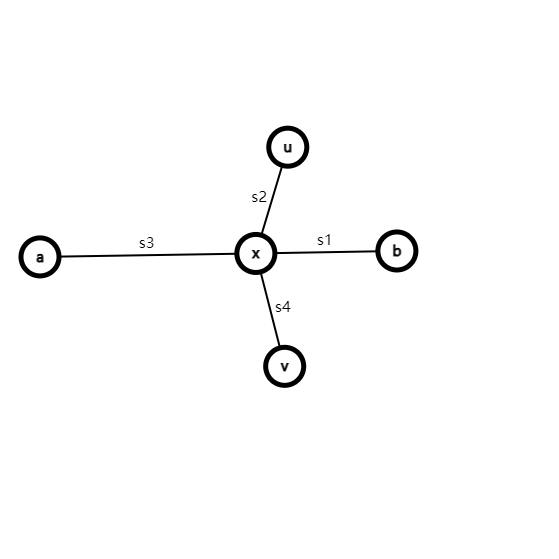
思路:令人痛心棘手的题,这里如果往二分想了就G了。这里证明下二分错误性!,如果假设二分区间个数越多,值越大,你就会发现如果最后一个为0,他其实被前面一点的1抵消更优,而你二分区间越小,值越大,只有一个区间时,答案为0,也不对,故这题二分不对。其实这种题应该用一种方法解决,自己总结为层次拆分法。显然发现增加一个断点,右边区间的值会再之前的基础上变大1.这就可以发现,如果我把每次操作视作增加一条从右端点连的线(选一个没选过的点作为后缀合左端点),如下图,就会发现你所有操作最后就是要形成这种图。既然我要形成这种图,而且我还优先满足k,那为什么不先选后缀合大的地方。于是直接求个后缀和,然后出了第一个点,其他排个序,每次贪心选最大的就好了。
例如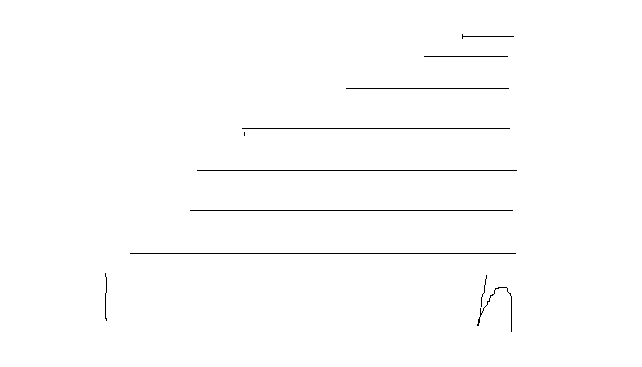
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
//#include<bits/stdc++.h>
#include <unordered_map>
#define ll long long
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
//const ll p=rnd()%mod;
ll ksm(ll x, ll y)
{ll ans = 1;while (y){if (y & 1){ans = ans % mod * (x % mod) % mod;}x = x % mod * (x % mod) % mod;y >>= 1;}return ans % mod % mod;
}
ll gcd(ll x, ll y)
{if (y == 0)return x;elsereturn gcd(y, x % y);
}
void fio()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
}
ll pre[250000];
int main()
{fio();ll t;cin>>t;while(t--){ll n,k;cin>>n>>k;string f;cin>>f;pre[f.size()]=0;ll ans=1;for(ll i=f.size()-1;i>=0;i--){ pre[i]=pre[i+1]+(f[i]=='0'?-1:1);}if(k==0){cout<<1<<endl;continue;}if(n!=1){sort(pre+1,pre+n);for(ll i=n-1;i>=1;i--){if(k<=0)break;k-=pre[i],ans++;}}if(k>0)cout<<-1<<endl;else cout<<ans<<endl;}return 0;
}
D. Recommendations
题面:
假设你在某个音频流媒体服务工作。该服务有 \(n\) 个活跃用户和 \(10^9\) 首曲目供用户收听。用户可以喜欢曲目,基于喜好,服务应该向他们推荐新的曲目。
曲目编号从 \(1\) 到 \(10^9\)。结果表明,第 \(i\) 个用户喜欢的曲目形成了一个区间 \([l_i, r_i]\)。
如果第 \(j\) 个用户(\(j \neq i\))喜欢第 \(i\) 个用户喜欢的所有曲目(并且,可能还包括一些其他的曲目),则称用户 \(j\) 是第 \(i\) 个用户的预测者。
另外,如果一首曲目尚未被第 \(i\) 个用户喜欢,但被第 \(i\) 个用户的所有预测者喜欢,则称这首曲目被强烈推荐给第 \(i\) 个用户。
计算每个用户 \(i\) 的强烈推荐曲目数量。如果一个用户没有任何预测者,则打印该用户为 \(0\)。
输入:
第一行包含一个整数 \(t\) (\(1 \le t \le 10^4\)) —— 测试用例的数量。接下来是 \(t\) 个测试用例。
每个测试用例的第一行包含一个整数 \(n\) (\(1 \le n \le 2 \cdot 10^5\)) —— 用户的数量。
接下来的 \(n\) 行每行包含两个整数 \(l_i\) 和 \(r_i\) (\(1 \le l_i \le r_i \le 10^9\)) —— 第 \(i\) 个用户喜欢的曲目区间。
额外的输入约束:所有测试用例中 \(n\) 的总和不超过 \(2 \cdot 10^5\)。
输出:
对于每个测试用例,打印 \(n\) 个整数,其中第 \(i\) 个整数是第 \(i\) 个用户的强烈推荐曲目数量(如果没有预测者,则为 \(0\))。
样例:
4
3
3 8
2 5
4 5
2
42 42
1 1000000000
3
42 42
1 1000000000
42 42
6
1 10
3 10
3 7
5 7
4 4
1 2
——————
0
0
1
999999999
0
0
0
0
0
2
3
2
4
8
思路:题目意思其实是求一个用户被其他用户完全包围的范围最小交区间的长度-用户本身范围的长度。不妨想想对于一个用户(l1,r1)来讲,如果所有区间(设为l,r)l小于他的都已经选出来了,那么此时我就只要去找到这些用户中r大于r1的最大l(\(l_{max}\)),然后保留满足(r>=r1)的最小\(r_{min}\)就好了,此时\(r_{min}\)-\(l_{max}\)+1-(r1-l1+1)就是答案。所以排个序(注意l相等时得r大的排在前面,因为他也是个约束),然后使用线段树去维护右边界(下标,离散化),线段树的值为所有已经遍历过的且刚好对应此r的最大l。然后用个set去存储之前遍历过的所有区间的右边界,每次问这个点时就先二分下,看下有没有符合的右值,没有答案自然为0,否则答案用线段树问下此时的最大左边界,计算得出答案。注意得用map记录相同左端点时的右端点,如果出现次数大于二,得把之前的答案设为0.最后答案就这样得出了,题目实现细节挺多的。
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
//#include<bits/stdc++.h>
#include <unordered_map>
#define ll long long
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
// const ll p=rnd()%mod;
const ll maxn=2e5+15;
ll ksm(ll x, ll y)
{ll ans = 1;while (y){if (y & 1){ans = ans % mod * (x % mod) % mod;}x = x % mod * (x % mod) % mod;y >>= 1;}return ans % mod % mod;
}
ll gcd(ll x, ll y)
{if (y == 0)return x;elsereturn gcd(y, x % y);
}
void fio()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
}
struct s
{ll l,r,v;
}p[maxn<<2];
void build(ll i,ll l,ll r)
{p[i].l=l,p[i].r=r;p[i].v=0;if(l==r)return ;build(i<<1,l,(l+r)>>1);build(i<<1|1,(l+r>>1)+1,r);
}
void xg(ll i,ll l,ll r,ll v)
{if(p[i].l==l&&p[i].r==r){p[i].v=max(v,p[i].v);return ;}ll mid=(p[i].l+p[i].r)>>1;if(l<=mid)xg(i<<1,l,min(mid,r),v);if(r>=mid+1)xg(i<<1|1,max(mid+1,l),r,v);p[i].v=max(p[i<<1].v,p[i<<1|1].v);
}
ll q(ll i,ll l,ll r)
{ll ans=0;if(p[i].l==l&&p[i].r==r){ans=p[i].v;return ans;}ll mid=(p[i].l+p[i].r)>>1;if(l<=mid)ans=max(ans,q(i<<1,l,min(mid,r)));if(r>=mid+1)ans=max(ans,q(i<<1|1,max(mid+1,l),r));return ans;
}
struct f1
{ll z,id;
};
vector<f1>g[250000];
ll ans[250000];
bool zm(f1 x,f1 y)
{return x.z>y.z;
}
int main()
{fio();ll t;cin>>t;while(t--){ll uop=0;set<ll>l,r;map<ll,ll>mp,mp1;ll n;cin>>n;ll ko=0;for(ll i=1;i<=n;i++){ll x,y;cin>>x>>y;l.insert(x);if(mp1[x]==0){ko++;mp1[x]=ko;g[ko].clear();}g[mp1[x]].push_back({y,i});r.insert(y);}for(auto j:l){sort(g[mp1[j]].begin(),g[mp1[j]].end(),zm);}ll cnt=0;for(auto j:r){cnt++;mp[j]=cnt;}build(1,1,cnt);//xg(1,2,2,2);//cout<<q(1,1,2)<<endl;r.clear();map<ll,ll>mu;for(auto j:l){mu.clear();ll u=mp1[j];for(auto z:g[u]){auto d=r.lower_bound(z.z);if(mu[z.z]>0){ans[mu[z.z]]=0;ans[z.id]=0;}else {if(d==r.end()){ans[z.id]=0;}else {ll k=q(1,mp[*d],cnt);ans[z.id]=j-k+*d-z.z;}}mu[z.z]=z.id;xg(1,mp[z.z],mp[z.z],j);r.insert(z.z);}}for(ll i=1;i<=n;i++)cout<<ans[i]<<endl;}
}