目录
- 拟牛顿法的思想
- 拟牛顿法的条件
- 拟牛顿法的步骤
- 校正矩阵的确定
- SR1 校正（对称秩 1 校正）
- DFP 校正
- BFGS 算法
拟牛顿法的思想
牛顿法的迭代方程为：
\[d_k = - (\nabla^2 f(x_k))^{-1} \nabla f(x_k)
\]
牛顿法的优缺点：
- 优点：局部二阶收敛，速度快。
- 缺点：每步都要计算 Hessian 矩阵 \(\nabla^2 f(x_k)\)，运算量大，还要求函数至少二阶连续可微。
拟牛顿法的核心思想：每步用 \(B_k\) 近似取代 \(\nabla^2 f(x_k)\)，其满足以下条件：
- 某种意义下，\(B_k \approx \nabla^2 f(x_k)\)
- \(B_k\) 对称且正定，以产生下降方向（即保持下降性）
- \(B_k\) 的更新与计算要简单，只需函数的一阶信息
拟牛顿法的条件
设 \(f(x)\) 是二阶连续可微函数，对 \(\nabla f(x)\) 在点 \(x_{k+1}\) 处进行一阶泰勒近似：
\[\nabla f(x) \approx \nabla f(x_{k+1}) + \nabla^2 f(x_{k+1}) (x-x_{k+1})
\]
令 \(x = x_k\)，则：
\[\nabla f(x_{k+1}) - \nabla f(x_k) \approx \nabla^2 f(x_{k+1}) (x_{k+1}-x_k)
\]
记：
- 位移差：\(s_k = x_{k+1}-x_k\)
- 梯度差：\(y_k = \nabla f(x_{k+1}) - \nabla f(x_k)\)
由此得到：
\[\nabla^2 f(x_{k+1}) s_k \approx y_k
\]
由拟牛顿法的思想，我们希望 \(B_{k+1}\) 满足：
\[B_{k+1} s_k \approx y_k
\]
令 \(H_{k+1} = B_{k+1}^{-1}\)，则有：
\[H_{k+1} y_k \approx s_k
\]
上述两个方程又被称为割线方程。
拟牛顿法的步骤
拟牛顿法：
- 第一步：选取初始点 \(x_0\)，\(H_0 = I\)，给定终止误差 \(\varepsilon > 0\) ，令 \(k=0\)
- 第二步：计算 \(\nabla f(x_k)\)，若 \(|| \nabla f(x_k) || \leq \varepsilon\)，停止迭代并输出 \(x^*=x_k\)；否则进行第三步
- 第三步（搜索方向）：计算搜索方向 \(d_k = -H_k \nabla f(x_k)\)
- 第四步（迭代更新）：计算 \(x_{k+1} = x_k + d_k\)
- 第五步（更新 \(H_k\)）：计算 \(H_{k+1} = g(H_k)\)
拟阻尼牛顿法：
- 第一步：选取初始点 \(x_0\)，\(H_0 = I\)，给定终止误差 \(\varepsilon > 0\) ，令 \(k=0\)
- 第二步：计算 \(\nabla f(x_k)\)，若 \(|| \nabla f(x_k) || \leq \varepsilon\)，停止迭代并输出 \(x^*=x_k\)；否则进行第三步
- 第三步（搜索方向）：计算搜索方向 \(d_k = -H_k \nabla f(x_k)\)
- 第四步（线搜索）：通过线搜索确定步长 \(\alpha_k\)
- 第五步（迭代更新）：计算 \(x_{k+1} = x_k + \alpha_k d_k\)
- 第六步（更新 \(H_k\)）：计算 \(H_{k+1} = g(H_k)\)
现在的关键要点是：如何更新 \(H_k\) 且保持其对称正定性以及计算简单？想法如下：
\[H_{k+1} = H_k + D_k 或 B_{k+1} = B_k + E_k
\]
其中要求 \(D_k\) 或 \(E_k\) 的生成要尽量简单，被称为校正矩阵。
校正矩阵的确定
SR1 校正（对称秩 1 校正）
为保证 \(D_k\) 是秩 1 矩阵且 \(H_k\) 对称，可设 \(D_k = \alpha u u^\top\)。将该式带入到割线方程中，经过一系列推导后可得 SR1 校正公式：
\[H_{k+1} =
\begin{cases}
H_k + \frac{(s_k-H_ky_k)(s_k-H_ky_k)^\top}{(s_k-H_ky_k)^\top y_k} ,\ &若 (s_k-H_ky_k)^\top y_k \neq 0 \\
H_k, \ &若 (s_k-H_ky_k)^\top y_k=0
\end{cases}
\]
其对偶式为：
\[B_{k+1} = B_k + \frac{(y_k-B_ks_k)(y_k-B_ks_k)^\top}{(y_k-B_ks_k)^\top s_k}
\]
注：
- SR1 校正产生的 \(H_{k+1}\) 满足对称性，但不一定正定，即搜索方向不一定是下降的；
- 无法保证 \((s_k-H_ky_k)^\top y_k > 0\)，导致 \(H_{k+1}\) 可能非正定。
DFP 校正
\(H_{k+1}\) 由 \(H_k\) 经对称秩 2 校正产生，即 \(D_k = \alpha u u^\top + \beta v v^\top\)。将该式带入到割线方程中，经过一系列推导后可得 DFP 校正公式：
\[H_{k+1} = H_k + \frac{s_k s_k^\top}{s_k^\top y_k} - \frac{H_ky_k (H_ky_k)^\top}{y^\top H_ky_k}
\]
DFP 校正产生的 \(H_{k+1}\) 满足对称性且正定。
注：
- \(s_k^\top y_k > 0\) 在实际应用中是容易满足的条件：
- 采用精确线搜索和非精确的 Wolfe-Powell 准则时，条件一定满足；
- 采用非精确的 Armijo-Goldstein 准则时，条件可能不满足，当不满足时直接令 \(H_{k+1} = H_k\)；
- 当求解大规模非线性优化时，\(H_k\) 可能越来越接近奇异矩阵，使得算法“卡住”；
- 如果求解二次正定优化问题时，令 \(H_0=I\)，则 DFP 算法是共轭梯度法。
BFGS 算法
与 DFP 的校正思路和过程类似，但 BFGS 构造的是 \(B_{k+1}\)，经过一系列推导后可得到 BFGS 的校正公式：
\[B_{k+1} = B_k + \frac{y_k y_k^\top}{y_k^\top s_k} - \frac{B_ks_k (B_ks_k)^\top}{s^\top B_ks_k}
\]
BFGS 校正产生的 \(B_{k+1}\) 满足对称性且正定。
注：
- \(y_k^\top s_k > 0\) 在实际应用中是容易满足的条件：
- 采用精确线搜索和非精确的 Wolfe-Powell 准则时，条件一定满足；
- 采用非精确的 Armijo-Goldstein 准则时，条件可能不满足，按如下公式进行更新（此式有现成图片，就懒得自己打一遍了）：
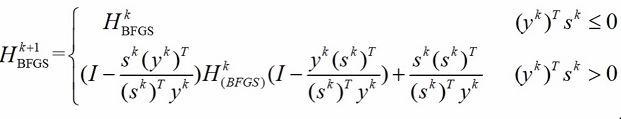
- 实际应用中，BFGS 更新 \(H_k\)，通过 \(d_{k+1} = - H_{k+1} \nabla f(x_{k+1})\) 产生下降方向。
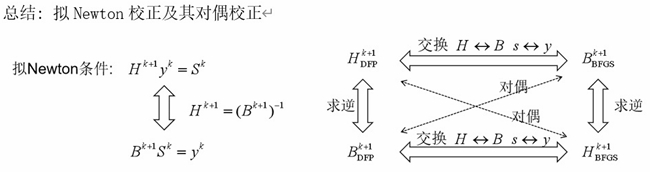
- BFGS 和 DFP 形式上是对偶的：
