如何计算多分类情况下的敏感性指标

1. 混淆矩阵cm，其中矩阵元素 cm[i][j] 表示真实标签为第 i 类且被预测为第 j 类的样本个数。

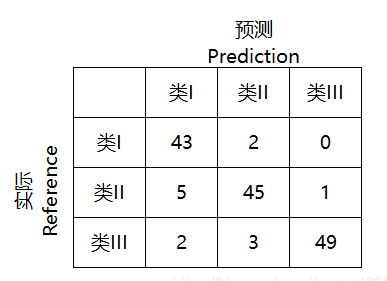
 2. TP, TN, FP, FN（以类II为例）

 

 

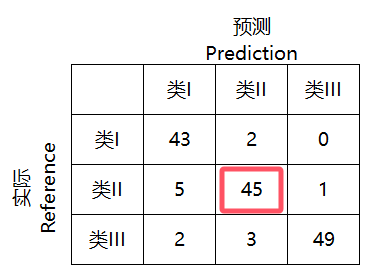
TP: 实际为正，预测为正（最中间这一格）

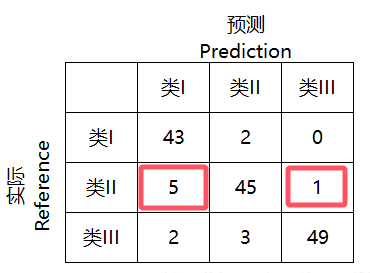
FN：实际为真，预测为假（中间这一排里面，挖去中间一格，剩下的格子）

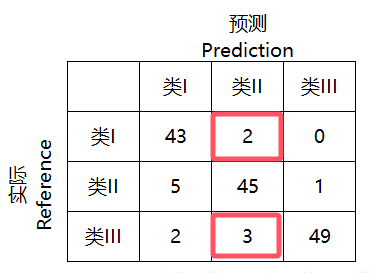
FP：实际为假，预测为真（中间这一列里，挖去中间一格，剩下的格子）

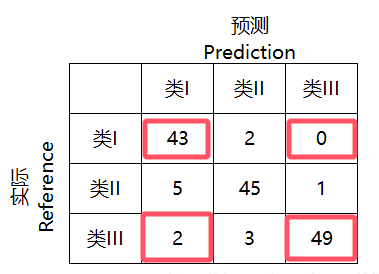
TN：实际为假，预测为假（整个矩阵挖去中间一列、中间一行）

3. 敏感性指标：

Overall Accuracy, Per-Class Accuracy, Recall, Precision, F1 Score 和 Specificity。

代码实现：

 

from sklearn.metrics import confusion_matrix
import numpy as npdef calculate_metrics(true_labels, pred_labels):"""手动计算分类指标，包括 Overall Accuracy, Per-Class Accuracy, Recall, Precision, F1 Score 和 Specificity。:param true_labels: List[int], 真实标签:param pred_labels: List[int], 预测标签:return: dict, 包含各指标的值"""# 初始化结果字典metrics = {"Overall Accuracy": None,"Per-Class Accuracy": {},"Recall": {},"Precision": {},"F1 Score": {},"Specificity": {}}# 总体 Accuracymetrics["Overall Accuracy"] = np.mean(np.array(true_labels) == np.array(pred_labels))# 计算混淆矩阵unique_labels = sorted(set(true_labels))  # 获取类别列表cm = confusion_matrix(true_labels, pred_labels, labels=unique_labels)# 矩阵元素 cm[i][j] 表示真实标签为第 i 类且被预测为第 j 类的样本个数。for i, label in enumerate(unique_labels):# TP, FP, FN, TN 的计算TP = cm[i, i]FP = sum(cm[:, i]) - TPFN = sum(cm[i, :]) - TPTN = cm.sum() - (TP + FP + FN)# 各指标的计算per_class_accuracy = (TP + TN) / cm.sum() if cm.sum() > 0 else 0.0  # 按类别的准确率recall = TP / (TP + FN) if (TP + FN) > 0 else 0.0  # Recall = TP / (TP + FN)precision = TP / (TP + FP) if (TP + FP) > 0 else 0.0  # Precision = TP / (TP + FP)specificity = TN / (TN + FP) if (TN + FP) > 0 else 0.0  # Specificity = TN / (TN + FP)f1_score = 2 * (precision * recall) / (precision + recall) if (precision + recall) > 0 else 0.0  # F1 = 2 * (P * R) / (P + R)# 存入字典metrics["Per-Class Accuracy"][label] = per_class_accuracymetrics["Recall"][label] = recallmetrics["Precision"][label] = precisionmetrics["F1 Score"][label] = f1_scoremetrics["Specificity"][label] = specificityreturn metrics# 测试函数
if __name__ == "__main__":true_labels = [0, 1, 2, 0, 1, 2, 1, 0, 2, 1]pred_labels = [0, 1, 2, 0, 0, 2, 1, 0, 2, 1]result = calculate_metrics(true_labels, pred_labels)print("Metrics:")for metric, values in result.items():if isinstance(values, dict):print(f"{metric}:")for label, value in values.items():print(f"  Class {label}: {value:.4f}")else:print(f"{metric}: {values:.4f}")