上一篇:《用人工智能模型预测股市和加密货币的K线图》
序言:预测时间序列,乍听之下似乎离我们普通人很遥远,甚至有些晦涩难懂。其实该技术早已渗透进了我们的日常生活。天气预报每天提醒你是否带伞、股市的波动影响你的投资决策、电力公司的负荷管理让你享受稳定的电网服务……这些无不依赖时间序列分析的强大力量。本篇将带你从最简单的预测方法出发,逐步揭开时间序列的面纱,让你看到这门技术是如何在普通人和机器学习这门高深技术之间架起一座桥梁
时间序列预测技术
在进入基于机器学习的预测(将在接下来的几章中详细讨论)之前,我们先来探索一些更加简单的预测方法。这些方法可以帮助您建立一个基准,用以衡量机器学习预测的准确性。
通过简单预测建立基准
预测时间序列的最基本方法是假设在时间 t+1t+1t+1 的预测值等于时间 ttt 的值,实际上就是将时间序列向前平移一个周期。
让我们从创建一个包含趋势、季节性和噪声的时间序列开始:
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""这是一个任意模式,您可以根据需要更改"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""在每个周期内重复相同的模式"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
time = np.arange(4 * 365 + 1, dtype="float32")
baseline = 10
series = trend(time, .05)
baseline = 10
amplitude = 15
slope = 0.09
noise_level = 6
创建时间序列
series = baseline + trend(time, slope) \
- seasonality(time, period=365, amplitude=amplitude)
加入噪声
series += noise(time, noise_level, seed=42)
绘制该序列后,您会看到类似图 9-6 的结果。
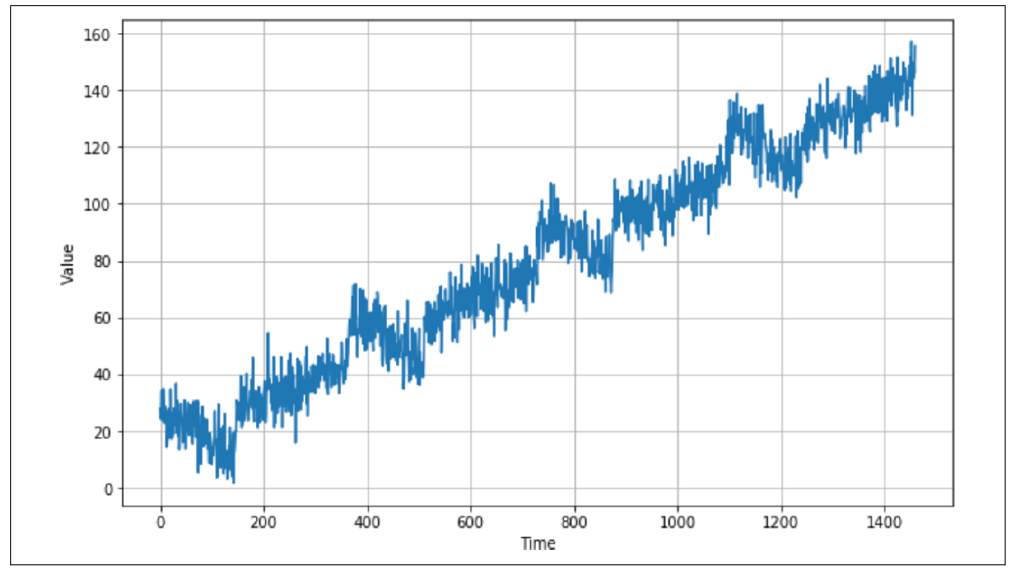
图 9-6:包含趋势、季节性和噪声的时间序列
现在你已经有了数据,可以像处理任何数据源一样,将其拆分为训练集、验证集和测试集。当数据中存在某种季节性特征时,就像在本例中看到的那样,在拆分时间序列时最好确保每个部分都包含完整的季节。因此,例如,如果你想将图 9-6 中的数据拆分为训练集和验证集,一个不错的拆分点可能是时间步 1000,这样训练数据包含到第 1000 步为止,而验证数据则从第 1000 步开始。
在这里你实际上并不需要进行拆分,因为你只是做一个简单的预测,每个时间步 ttt 的值仅仅是时间步 t−1t-1t−1 的值。但为了便于接下来的几个图表说明,我们将聚焦于从时间步 1000 开始的数据。
要从某个分割时间点开始预测序列,这个时间点存储在变量 split_time 中,你可以使用如下代码:
naive_forecast = series[split_time - 1:-1]
图 9-7 显示了验证集(从时间步 1000 开始,split_time 设置为 1000)及其叠加的简单预测结果。
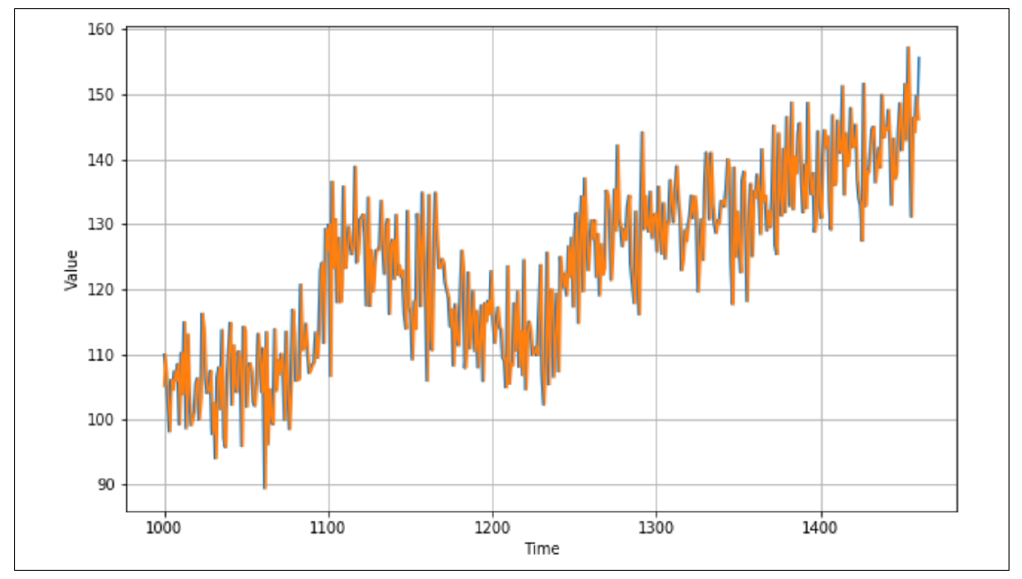
图 9-7:时间序列上的简单预测
看起来效果相当不错——预测值和实际值之间有一定关系,并且在时间轴上绘制时,预测值与原始值似乎非常接近。但你会如何衡量这种预测的准确性呢?
衡量预测准确性
有多种方法可以衡量预测的准确性,但我们将重点关注其中两种:均方误差(MSE)和平均绝对误差(MAE)。
• 对于 MSE,你只需计算时间 ttt 上预测值与实际值的差异,将其平方(以去掉负值),然后计算这些平方差的平均值。
• 对于 MAE,你计算时间 ttt 上预测值与实际值的差异,取绝对值(代替平方以去掉负值),然后计算这些绝对差值的平均值。
对于我们基于合成时间序列创建的简单预测,可以使用以下代码计算 MSE 和 MAE:
print(keras.metrics.mean_squared_error(x_valid, naive_forecast).numpy())
print(keras.metrics.mean_absolute_error(x_valid, naive_forecast).numpy())
我得到了一个 MSE 值为 76.47,一个 MAE 值为 6.89。像任何预测一样,如果你能降低误差,就可以提高预测的准确性。接下来我们看看如何实现这一点。
更少的简单预测:使用移动平均进行预测
之前的简单预测方法是将时间 t−1t-1t−1 的值作为时间 ttt 的预测值。使用移动平均的方法类似,但不是只取时间 t−1t-1t−1 的值,而是取一组值(比如 30 个),计算它们的平均值,并将其作为时间 ttt 的预测值。以下是代码实现:
def moving_average_forecast(series, window_size):
"""预测最近一组值的平均值。
如果 window_size=1,则等同于简单预测"""
forecast = []
for time in range(len(series) - window_size):
forecast.append(series[time:time + window_size].mean())
return np.array(forecast)
moving_avg = moving_average_forecast(series, 30)[split_time - 30:]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, moving_avg)
图 9-8 显示了移动平均值与数据的对比。

图 9-8:绘制移动平均值
在我绘制这个时间序列后,得到了 MSE 值为 49 和 MAE 值为 5.5。因此,预测准确性确实有所提升。但这种方法没有考虑到趋势或季节性,因此通过一些分析,我们可能还能进一步改进预测。
改进移动平均分析
鉴于这个时间序列的季节周期是 365 天,你可以使用一种叫做“差分”的技术来平滑趋势和季节性。差分的做法是将时间 ttt 的值减去时间 t−365t-365t−365 的值。这将使图形变得平坦。以下是代码:
diff_series = (series[365:] - series[:-365])
diff_time = time[365:]
现在你可以计算这些差分值的移动平均值,并将过去的值加回来:
diff_moving_avg = moving_average_forecast(diff_series, 50)[split_time - 365 - 50:]
diff_moving_avg_plus_smooth_past = moving_average_forecast(series[split_time - 370:-360], 10) + diff_moving_avg
绘制该结果(参见图 9-9)后,你会发现预测值已有明显改进:趋势线非常接近实际值,尽管噪声被平滑了。季节性和趋势都得到了有效反映。
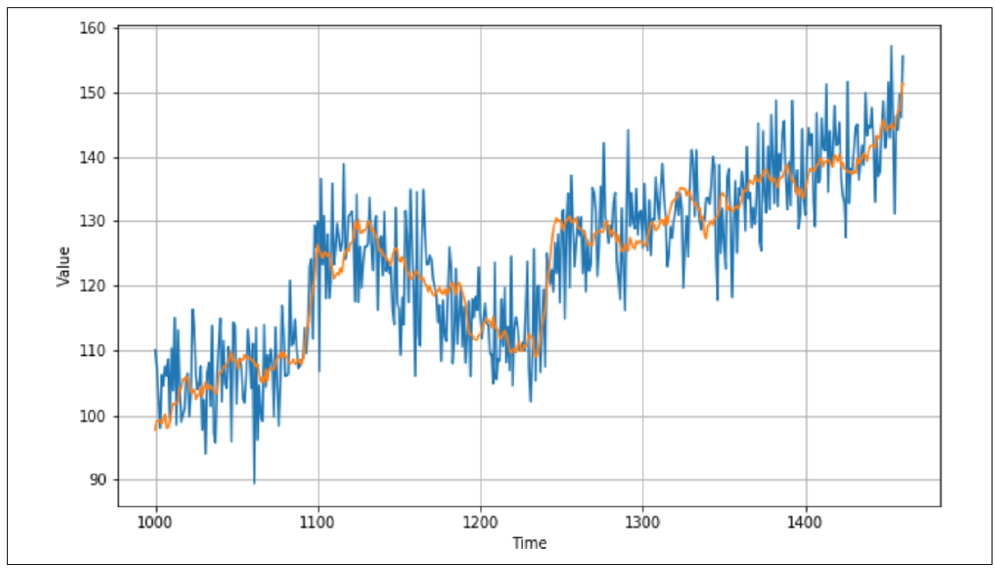
图 9-9:改进的移动平均值
通过计算 MSE 和 MAE,这一改进的效果得到了进一步验证——在本例中,我得到了 MSE 值为 40.9 和 MAE 值为 5.13,显示出预测的明显提升。
总结
本章介绍了时间序列数据及其一些常见属性。你创建了一个合成的时间序列,并学习了如何对其进行简单预测。从这些预测中,你使用均方误差(MSE)和平均绝对误差(MAE)建立了基准测量。这是一个从 TensorFlow 的短暂休息,但在下一章中,你将重新使用 TensorFlow 和机器学习,看看是否能进一步提高预测的准确性!