- 进入实模式 (英特尔芯片 传统:16位 简单 模式)
- 跳转到 BIOS(基本输入输出系统)(ROM 固化,自检,初始化)
- 加载引导代码 boot程序 到 内存0x7c00处开始运行,(内存空间:上高地址,下低地址),向上运行 + 偏移量 (空间 512B)
- 需要设计部分:检测、内存空间变化 由 16位保护模式 切换到 64位等保护模式,加载 硬盘上的操作系统并运行
- 通过引导程序进入操作系统
Linux 系统基本开机过程记录
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/855624.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
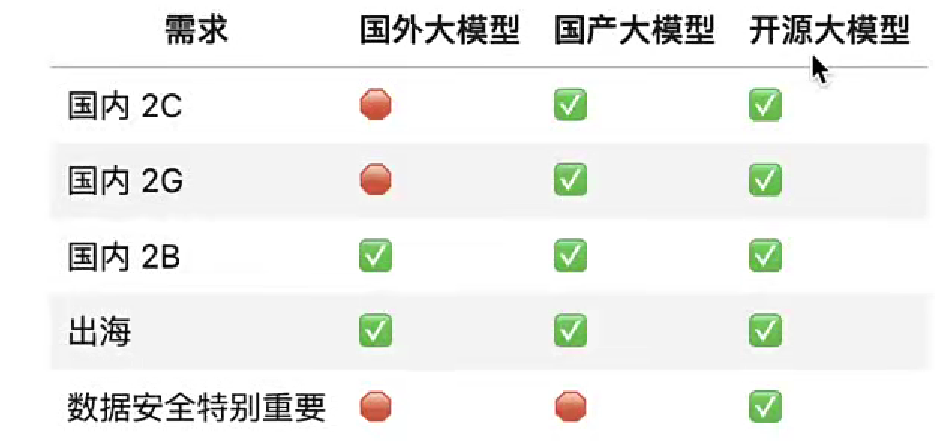
1大模型应用开发基础
一、目标
懂得AI,懂得编程、懂得业务的超级个体,将会是AGI时代最重要的人。
AI使得一个人能够干多个人的活
想要做到“AI全栈”需要涉及的知识面是非常广泛的,单单学习一门课程是不能全部涉及的
我们首先需要做的是入门,后面走的深入,走的远只能靠自己,依靠社群,和AI的进…
grpc安装(windows or Linux)
grpc安装(windows or Linux)
下载源码
这里使用 gRPC 最新版本源代码进行编译和安装,版本号为 v1.50.0, 以下为安装步骤:
一、使用Git克隆gRPC到本地
在终端中打开某一文件夹,建议新建一个单独存放 gRPC 源代码的文件夹,输入:
git clone -b v1.50.0 https://github.com/…
Golang内存模型与源码解析
0、引言
本篇笔记用于记录作者在学习Golang的GC模型之前,对Golang内存模型的学习。目前使用的Go版本为1.22.4
1、Golang内存管理宏观结构
假设我们每次向内存池申请空间时,都需要频繁地向操作系统发出请求,这不仅会增加内存分配的时间,还可能引入竞争和锁的开销,从而导致性…
全场景一站式2024最新vmware环境下安装win7并且破解QTP
目录VMwareVMware和Ubuntu下载链接下载Win 7 系统各个操作系统网站激活码是什么查看是否激活激活操作vmware下安装ubuntu创建虚拟机下载VMtool灰色灰色按键点击不了下载提示有问题原因文件传递共享文件借助外界U盘有了VMTool就可以直接拖拽!!!!有了VMTool就可以全屏化——倒…
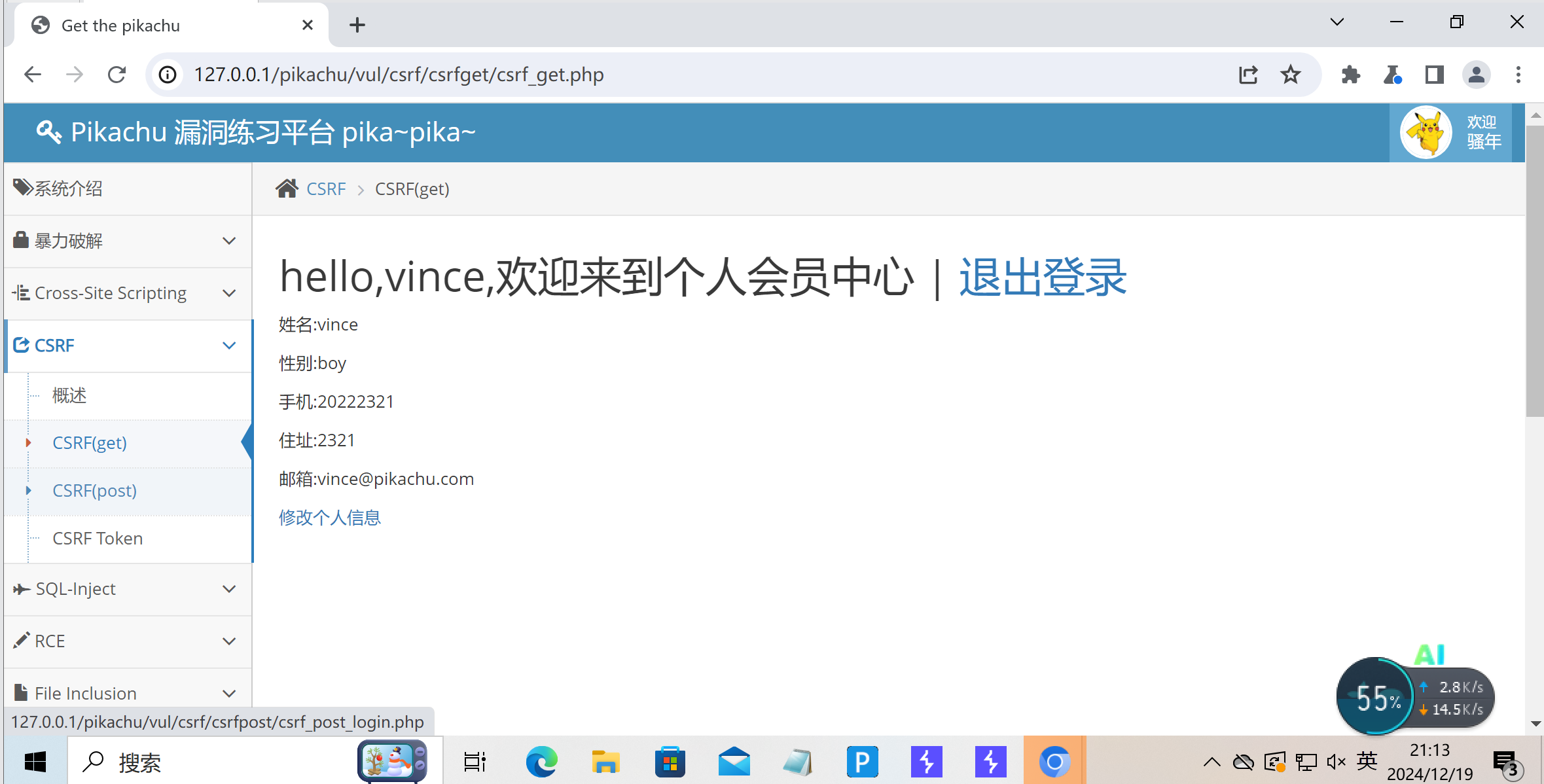
20222321 2024-2025-1 《网络与系统攻防技术》实验八实验报告
一.实验内容
(1)Web前端HTML
能正常安装、启停Apache。理解HTML,理解表单,理解GET与POST方法,编写一个含有表单的HTML。
(2)Web前端javascipt
理解JavaScript的基本功能,理解DOM。
在(1)的基础上,编写JavaScript验证用户名、密码的规则。在用户点击登陆按钮后回显“欢迎…
LVGL学习 - Visual Studio外部“.c.h”文件添加
LVGL项目工程添加“.c.h”文件后 “C1083”“LNK2019”报错的解决方法一、首先把文件添加至工程,现有项选择所需添加的“.c.h”文件但还是会有如下报错,解决方法在第2步。二、“.c”文件需要添加“extern "C"”
下图截至官方文档我试了只添加“extern "C"…
组合数学+ybt题解
加法原理
乘法原理
排列数
从 \(n\) 个数中任取 \(m\) 个元素的排列的方案数,表示为 \(A^m_n=\frac{n!}{(n-m)!}\)
\(0!=1\)
全排列 \(A^n_n\)
组合数
从 \(n\) 个元素中取出 \(m\) 个元素的组合的个数,表示为 \(\dbinom{n}{m}= \frac{A^m_n}{m!}=\frac{n!}{m!(n-m)!}\)
如何…