洛谷P11411兰奇的卡牌游戏
传送锚点
摸鱼环节
兰奇的卡牌游戏
题目描述
作为制卡大师的兰奇,发明了一种自助型卡牌游戏。
给定 \(n\) 张卡牌,第 \(i\) 张卡牌编号为 \(i\),其权值为 \(a_i\),卡牌的权值互不相同。
这个卡牌游戏的规则需要自己生成。一开始,所有的牌都在备选区。从备选区中选取一张编号最小的卡牌放到手牌区,便可进入规则生成阶段。
规则生成阶段的步骤如下:
-
将手牌区的任意一张牌弃置到废牌区之中。
-
然后在备选区中选择一张编号和权值均大于当前弃牌的牌,加入手牌区。若存在这样的一张牌,则称这张牌与弃牌互为置换;若不存在这样的一张牌,则跳过当前步骤。
-
继续从备选区中选择一张编号大于当前弃牌且权值小于当前弃牌的牌,加入手牌区。若存在这样的一张牌,则同样可称这张牌与弃牌互为置换;若不存在这样的一张牌,则跳过当前步骤。
-
完成以上步骤后,若手牌区没有卡牌了,则规则生成阶段结束。若仍有卡牌,则继续重复上述步骤,直到手牌区没有卡牌。
为了保证生成置换的唯一性,兰奇规定规则生成阶段合法当且仅当规则生成结束后,所有的牌都在废牌区。并且在正式游戏阶段一张编号较大的牌经过一系列操作后得到一张编号较小的牌后,该编号较大的牌,均要满足能够有机会按照在手牌区出现过的该张编号较小的牌的弃牌后生成的置换相同的步骤在规则生成阶段成为编号较小的牌的置换;若手牌区未出现该张编号较小的牌的弃牌后生成的置换,则无需考虑。否则,生成的置换是无效的。
可以证明在规则生成阶段合法的情况下,每张卡牌可以与哪些卡牌互为置换的方案是唯一的。
正式游戏阶段的步骤如下:
-
选择任意一张卡牌作为起始卡牌并加入手牌区,然后进入下一步骤。
-
将前手牌区的卡牌弃入废牌堆,然后从备选区中选择一张该卡牌的置换加入手牌区。若当前弃置的卡牌在备选区没有置换,则正式游戏阶段结束;反之,则得分增加 \(1\) 分,然后继续重复步骤 2。
游戏发售后,销量并不是很好。因为游戏规则太复杂了。玩家们希望删去一些卡牌,使得正式游戏阶段的最大得分不超过 \(k\)。
而兰奇为了保证游戏的不做太大的改动,他要求删去一些卡牌后,保留下来的任意一张卡牌重新生成的置换要与原来未删去卡牌情况下的置换相同。
删去后置换仍相同的定义是:设 \(S\) 表示某一张卡牌,未删除任何一张卡牌时的置换集合;\(T\) 表示该张卡牌,在删除了部分卡牌时的置换集合。此时,满足 \(T \subseteq S\)。则称删去部分卡牌后,该卡牌的置换与原来未删去卡牌情况下的置换相同。
兰奇想知道,在满足了玩家和自己的要求的前提下,他最少要删除几张卡片。
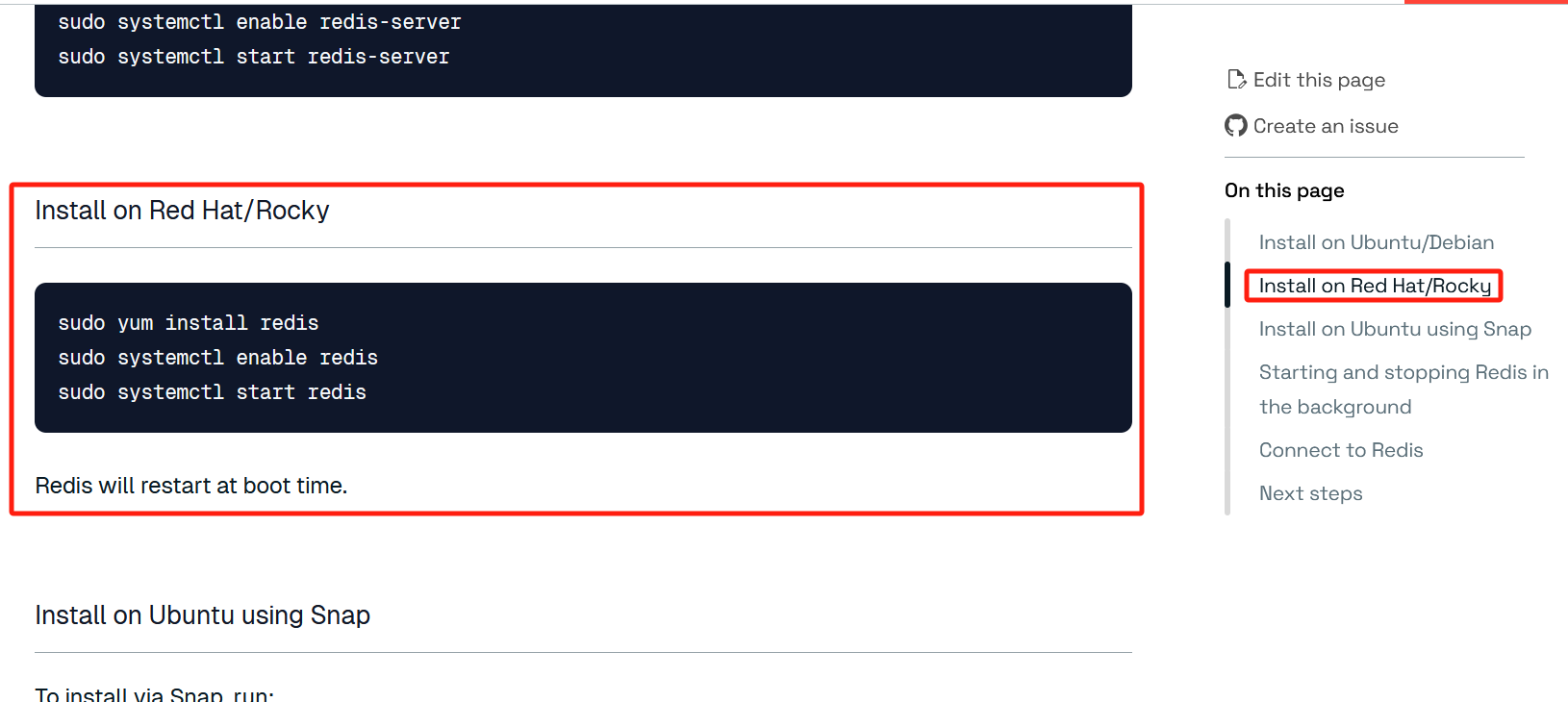
输入格式
第一行输入两个正整数 \(n\) 和 \(k\),分别表示卡牌的数量和正式游戏阶段的最大得分不能超过的值。
第二行输入 \(n\) 个元素,第 \(i\) 个元素 \(a_i\),表示编号为 \(i\) 的卡牌权值。
输出格式
输出一个正整数,表示在满足玩家和自己的要求的前提下,最少要删除几张卡片。
样例 #1
样例输入 #1
3 2
1 2 3
样例输出 #1
0
样例 #2
样例输入 #2
6 2
3 2 7 99 10 15
样例输出 #2
3
提示
【样例1解释】
编号为 \(1\) 的卡牌与编号为 \(2\) 的卡牌互为置换,编号为 \(2\) 的卡牌与编号为 \(3\) 的卡牌互为置换。
所以,在不删去的情况下,获得最大得分的方案是:用编号为 \(1\) 的卡牌作为起始卡牌置换出编号为 \(2\) 的卡牌,然后再置换出编号为 \(3\) 的卡牌。该方案的最大得分为 \(2\),所以不需要删除任何一张卡牌。
【数据范围】
本题采用捆绑测试。
- Subtask 1(15 points):\(n \le 10\)。
- Subtask 2(5 points):\(k = n\)。
- Subtask 3(80 points):无特殊限制。
对于所有测试数据,\(1 \le n \le 2000\),\(1 \le a_i \le 10^9\)。
大型阅读理解,OI已经卷到考语文了?
我们需要冷静得阅(da)读(kai)题面(jie),然后惊奇的发现居然没有题解(毕竟只有暂时8个人AC)。
正片开始
Reading部分(最难的一步)
经过通读题面,我们可以很轻(jian)松(nan)地发现弃牌和选牌的过程可以构建成一棵树,然后按照规则来就可以再一次很轻松(bushi)地发现这是一棵名为笛卡尔树的树。(不会笛卡尔树可参考这篇)。
接着阅读下文就可以发现,这是在一棵笛卡尔树上删点,要求树上任意两点的距离不超过\(\frac{k}{2}\),求所删的点的最小数目。
Thinking部分
显然笛卡尔树肯定是要建的,接下来要处理两点间的距离关系,偷瞄一眼数据量,发现\(1 \le n \le 2000\)显然支持\(O(n^{2})\)的算法。这样我们就可暴力枚举点对进行删除操作,至于两点间的距离显然可以用\(LCA\)处理,然后就\(AC\)了。
Just Do It部分
- 首先需要建出美丽的笛卡尔树
void build()
{stack<int>s;//用单调栈O(n)实现for(int i=1;i<=n;i++){while(!s.empty()&&frz[s.top()].b>frz[i].b){l_son[i]=s.top();s.pop();}if(!s.empty())r_son[s.top()]=i;s.push(i);}while(!s.empty())//压在最底下的rt就是根节点{rt=s.top();s.pop();}
}
- 为了简洁明了,转存邻接表。(
脑子不够用)
void rebuild()//重建
{for(int i=1;i<=n;i++){if(l_son[i]){g[i].push_back(l_son[i]);g[l_son[i]].push_back(i);}if(r_son[i]){g[i].push_back(r_son[i]);g[r_son[i]].push_back(i);}}
}
- 求\(LAC\)(为了美观可以将求\(path\)长度打包成函数)
void dfs(int u,int fa)//dep深度数组处理
{dep[u]=dep[fa]+1;f[u][0]=fa;for(auto v:g[u])if(v!=fa) dfs(v,u);
}
void bz()//倍增信息处理
{dfs(rt,0);for(int j=1;j<20;j++)for(int i=1;i<=n;i++)f[i][j]=f[f[i][j-1]][j-1];
}
int LCA(int x,int y)//求LCA
{if(dep[x]<dep[y])swap(x,y);//dep[x]>=dep[y],跳yint dis=dep[x]-dep[y];for(int i=0;i<11;i++)if(dis>>i&1) x=f[x][i];if(x==y) return x;for(int i=10;i>=0;i--)if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];return f[x][0];
}
int path(int x,int y)//两点间的距离
{return max(0*1ll,dep[x]+dep[y]-2*dep[LCA(x,y)]);
}
- 分讨\(k\)的奇偶性(\(k\)为奇数时需考虑相邻点)
if(k%2==0)
{int sd=k/2;for(int i=1;i<=n;i++){int cnt=0;for(int j=1;j<=n;j++){int ad=path(i,j);cnt+=(ad>sd?1:0);}ans=min(ans,cnt);}write(ans);
}
else
{int sd=k/2;for(int i=1;i<=n;i++){for(auto v:g[i]){int cnt=0;for(int j=1;j<=n;j++){int ad=path(i,j),ad2=path(v,j);cnt+=(ad>sd&&ad2>sd?1:0);}ans=min(ans,cnt);}}write(ans);
}
-
细节方面:
- 笛卡尔树需要以权值为第一关键字(权值可大可小),编号单调为第二关键字。
- 如果一不小心
TLE可以尝试快读快写。
完整代码
#ifdef ONLINE_JUDGE
#else
#define Qiu_Cheng
#endif
#include <bits/stdc++.h>
#define int long long
using namespace std;
// typedef long long ll;
const int N=1e7+50,M=1e5+5,mod=1e9+7;
inline int read()
{int x=0,f=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-'0');c=getchar();}return x*f;
}
inline void write(int x)
{if(x<0){putchar('-');x=-x;}if(x>9) write(x/10);putchar(x%10+'0');
}
const double pi=acos(-1);
int n,k,rt;
struct node
{int a,b;//编号,权值
}frz[N];
bool cmp(node a,node b){return a.a<b.a;}
int r_son[N],l_son[N];
void build()
{stack<int>s;for(int i=1;i<=n;i++){while(!s.empty()&&frz[s.top()].b>frz[i].b){l_son[i]=s.top();s.pop();}if(!s.empty())r_son[s.top()]=i;s.push(i);}while(!s.empty()){rt=s.top();s.pop();}
}
vector<int>g[N];
void rebuild()
{for(int i=1;i<=n;i++){if(l_son[i]){g[i].push_back(l_son[i]);g[l_son[i]].push_back(i);}if(r_son[i]){g[i].push_back(r_son[i]);g[r_son[i]].push_back(i);}}
}
int f[2005][32];//倍增信息
int dep[N];//点深度
void dfs(int u,int fa)
{dep[u]=dep[fa]+1;f[u][0]=fa;for(auto v:g[u])if(v!=fa) dfs(v,u);
}
void bz()
{dfs(rt,0);for(int j=1;j<20;j++)for(int i=1;i<=n;i++)f[i][j]=f[f[i][j-1]][j-1];
}
int LCA(int x,int y)
{if(dep[x]<dep[y])swap(x,y);//dep[x]>=dep[y],跳yint dis=dep[x]-dep[y];for(int i=0;i<11;i++)if(dis>>i&1) x=f[x][i];if(x==y) return x;for(int i=10;i>=0;i--)if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];return f[x][0];
}
int path(int x,int y)
{return max(0*1ll,dep[x]+dep[y]-2*dep[LCA(x,y)]);
}
inline void solve()
{ n=read();k=read();for(int i=1;i<=n;i++) frz[i].a=read(),frz[i].b=i;sort(frz+1,frz+n+1,cmp);build();rebuild();bz();int ans=1e9+7;if(k%2==0){int sd=k/2;for(int i=1;i<=n;i++){int cnt=0;for(int j=1;j<=n;j++){int ad=path(i,j);cnt+=(ad>sd?1:0);}ans=min(ans,cnt);}write(ans);}else{int sd=k/2;for(int i=1;i<=n;i++){for(auto v:g[i]){int cnt=0;for(int j=1;j<=n;j++){int ad=path(i,j),ad2=path(v,j);cnt+=(ad>sd&&ad2>sd?1:0);}ans=min(ans,cnt);}}write(ans);}
}
signed main()
{
#ifdef Qiu_Chengfreopen("1.in","r",stdin);freopen("1.out","w",stdout);
#endifios::sync_with_stdio(false);cin.tie(0);cout.tie(0);// int Tt;// cin>>Tt;// while(Tt--)solve();solve();return 0;
}// 6666 66666 666666
// 6 6 6 6 6
// 6 6 6666 6
// 6 6 6 6 6
// 6666 6 6 6666666//g++ -O2 -std=c++14 -Wall "-Wl,--stack= 536870912 " cao.cpp -o cao.exe
完结收工!!!!!

个人主页
看完点赞,养成习惯
\(\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\)