不难发现循环节长度为60,预处理前60项即可,下为证明。
注意到\(F_{15}\equiv F_0 \,(mod \,10)\),由斐波那契性质\(F_n=F_{n-1}+F_{n-2}\)。
得到\(F_{16}=F_{15}+F_{14},F_{17}=F_{16}+F_{15},F_{18}=F_{17}+F_{16}\)
\(F_{15}\equiv 0 \cdot F_{14},F_{16}\equiv 1 \cdot F_{14},F_{17}\equiv 1 \cdot F_{14},...\)
\(F_{15}\equiv F_{0} \cdot F_{14},F_{16}\equiv F_{1} \cdot F_{14},F_{17}\equiv F_{2} \cdot F_{14},...\)
可以推出公式\(F_n\equiv F_{14}^{\lfloor \frac{n}{15}\rfloor}\cdot F_{n\%15} \,(mod \,10)\)
可以知道\(F_{n\%15}\)的循环节长度为15。
由于\(F_{14}\equiv 7\,(mod \,10)\),接下来考虑\(7^n\%10\)的循环节。
显然\(7^4\equiv 1 \,(mod \,10)\),所以\(7^n\%10\)的循环节长度为4。
综上所述,\(F_{15}\equiv F_0 \,(mod \,10)\)的循环节长度为60.
证明
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/856599.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
【安全评审】“2024网络安全100强-行业应用”评分全流程细则
一 指标理解1.1 “行业应用”的核心优势是什么?1.2 评估维度有哪些?二、评审专家筛选2.1 对专家所在单位有什么要求?2.2 对专家所在行业有什么要求?2.3 对专家个人能力有什么要求?2.4 对专家组有什么要求?2.5 对专家个人价值观有什么要求?三、评分规则制定3.1 “典型案例…
《计算机组成及汇编语言原理》阅读笔记:p9-p27
《计算机组成及汇编语言原理》学习第 2 天,p9-p27 总结,总计 19 页。
一、技术总结
1.quantum physics(量子物理学)
(1)quantum(量子)
quantum的本意是:c. the smallest amount of sth(量子)。
In physics, a quantum is the minimum amount of any physical entity (physi…
第4章 C#的高级特性
第4章 C#的高级特性
4.1 委托
4.1.2 多播委托
对值为 null 的委托变量进行 + 或 += 操作,等价于为变量指定一个新值:
SomeDelegate d = null;
d += SomeMethod1; // 等价于 d = SomeMethod1委托是 不可变 的,因此调用 += 和 -= 的实质是 创建一个新的委托实例 ,…
使用frida分析白盒aes,DFA攻击
这次分析的app是:五菱汽车(8.2.1)
登录,抓包发现请求体只有sd字段,看见加密的时候,可以先使用算法助手hook java层所有加解密方法发现我们所需要的sd加密字段在java层hook不到,那加密算法应该是写在了so层,因为这个app是bb加固企业,得有脱壳机才能脱。
jadx加载dex,直接…
2024 golang安装使用详细教程以及常见问题处理(附激活至2099年)
GoLand 简介
GoLand 是一款非常强大的 Go 语言集成开发环境,由JetBrains公司开发。它提供了丰富的功能和工具,帮助开发者更高效地编写、调试和部署代码。
下面这种方式仅供交流学习,如果有能力还请支持正版
下载安装
为了方便,也可以去链接取
点击获取安装包开始安装下载完成…
Infinite Pixels(无限像素)第五次作业
这个作业属于哪个课程
https://edu.cnblogs.com/campus/zjlg/rjjc这个作业的目标
小组成员分工完成选题的软件设计组长
祝方略-2022329301131组员1
娄涵格-2022329301112组员2
颜宇航-2022329301125组员3
常佳鑫-2022329301071一、团队介绍团队名称:Infinite Pixels(无限像素…
CMake构建学习笔记19-OpenSSL库的构建
详细介绍了在Windows和Linux环境下构建OpenSSL库的方法,并且如何通过CMake的方式被主程序调用。1. 概述
OpenSSL是一个开源的加密工具包和库,主要实现了安全套接字层(SSL)和传输层安全(TLS)协议,以及各种加密算法、数字签名、消息摘要、加密证书等功能。这个库可以说是W…
概率论沉思录:初等假设检验
我们在上一篇博客中介绍了传统的抽样理论。其中,我们导出了几种经典的抽样分布,也即给定关于所观察现象的假设H,数据D的概率分布p(D | H)。在上一篇博客中提到的伯努利坛子模型中,假设H即坛子的内容,数据D即重复抽球所生成的红球和白球序列。但正如我们我们在上一篇博客的…
开启Word、Excel、PPT时速度很慢的一种解决方法
本文介绍基于修改加载项,解决Microsoft Office系列软件开启速度较慢的办法~本文介绍基于修改加载项,解决Microsoft Office系列软件开启速度较慢的办法。最近,发现Excel软件的打开速度越来越慢,会在一定程度上影响工作效率。因此尝试对此加以解决。其中,本文所给方法对于Wo…
2024-2025-1 学号20241315《计算机基础与程序设计》第十三周学习总结
作业信息这个作业属于哪个课程
<班级的链接>2024-2025-1-计算机基础与程序设计)这个作业要求在哪里
<作业要求的链接>https://www.cnblogs.com/rocedu/p/9577842.html#WEEK13这个作业的目标
<写上具体方面>第12章并完成云班课测试作业正文
... 本博客链接 h…
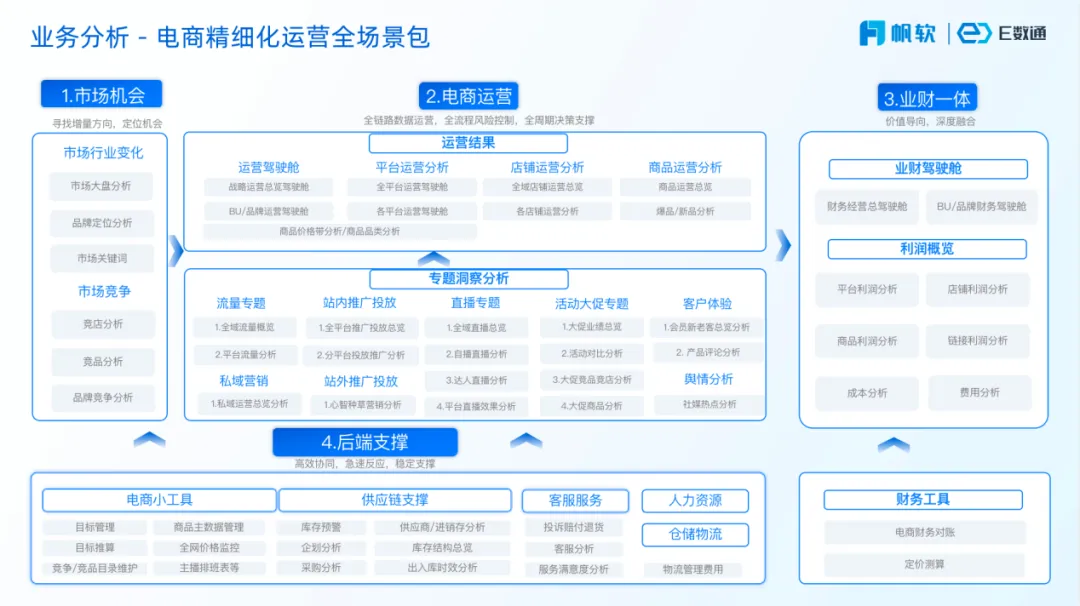
【解决方案】电商精细化运营方案
随着互联网技术的不断发展和普及,电商行业在过去几十年中取得了巨大的发展和变革。从供小于求的“以商品为主”阶段,到享受时代红利的“以流量为主”阶段,再到重视消费者体验的“精细化运营”阶段,电商市场正在进入以消费者为中心精细化运营时代,这要求电商企业从存量市场…
洛谷 P11411 兰奇的卡牌游戏——题解
洛谷P11411兰奇的卡牌游戏传送锚点摸鱼环节
兰奇的卡牌游戏
题目描述
作为制卡大师的兰奇,发明了一种自助型卡牌游戏。
给定 \(n\) 张卡牌,第 \(i\) 张卡牌编号为 \(i\),其权值为 \(a_i\),卡牌的权值互不相同。
这个卡牌游戏的规则需要自己生成。一开始,所有的牌都在备选区…