网络流,梳理一下然后看下 trick。
网络流主要难点在于建模,网络流很多 trick 现在已经很难有新意了。很多很好想的都是紫题,没啥含金量啊。
最大流
在残量网络中找到一条路径,设边集为 \(u\),要求满足 \(\min_{ x\in u} C_x ≠ 0\),即每条边残量皆不为 \(0\)。此时将这条路径流满,流量就会变大,一直到没有增广路时即为本图最大流。
· Dinic
注意需要反建边,才能保证结果正确。代码中的一些小 skill 值得注意。
- 使用 bfs 从源点进行一次分层,即求单源最短路。
- 使用 dfs 在图上多路增广。
- 如果没有增广路了,那么退出,否则回到 1
有一些优化。
- 当前弧优化:对于每一条已经流满了流量的边,记录下来,本次增广内不再访问。将一次增广时间复杂度严格控制到 \(O(nm)\) 以内。
- 点优化:对于一个已经流不出流量的点,记录下来,本次增广内不再访问。
- bfs 分层优化:一次分层中已经走到了汇点,则停止。
code :
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=5010,N=210,inf=2e10;
int cnt,dis[N],first[N],head[N],ans;
int n,m,s,t;
bool vis[N];
struct edge
{int to,next,f;
}e[M*2];
void add(int u,int v,int w)
{e[++cnt].to=v;e[cnt].f=w;e[cnt].next=first[u];first[u]=cnt;e[++cnt].to=u;e[cnt].f=0;e[cnt].next=first[v];first[v]=cnt;
}
bool bfs(int u,int t)
{memset(vis,0,sizeof(vis));for(int i=1;i<=n;i++)head[i]=first[i];queue<int> q;q.push(u);dis[u]=1;vis[u]=1;while(!q.empty()){int now=q.front();q.pop();for(int i=first[now];i;i=e[i].next){int to=e[i].to;if(!vis[to]&&e[i].f>0){q.push(to);vis[to]=1;dis[to]=dis[now]+1;if(to==t)return 1;}}}return 0;
}
int dfs(int now,int t,int flow)
{if(now==t)return flow;int temp=flow;for(int i=head[now];i;i=e[i].next){int to=e[i].to;head[now]=i;if(e[i].f>0&&dis[to]==dis[now]+1){int k=dfs(to,t,min(e[i].f,flow));if(k==0)dis[to]=inf;e[i].f-=k;e[i^1].f+=k;flow-=k;if(flow==0)return temp;}}return temp-flow;
}
signed main()
{cin>>n>>m>>s>>t;cnt=1;for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;add(u,v,w);}while(bfs(s,t)){ans+=dfs(s,t,inf);}cout<<ans;return 0;
}
最小割
割:割掉一些边使得源汇不连通。
最大流 = 最小割
证明:
- 最大流 \(\leq\) 最小割。所有的割必然要对流的每个路径上中的一条边割掉,所以所有的割必然大于等于最大流。
- 最大流 \(\ge\) 最小割。考虑我们求出了一个最大流,那么某些边残量网络上为 \(0\)。这些边一定分布成为一个割,否则仍然会有增广路。
最小割 = 最大流
费用流
将增广算法改成 dijkstra。将边权改为费用分层。
但是残量网络中可能存在负权边,所以需要用到一个势能 \(h\)。让 \(u\to v\) 的边权由 \(x\) 变为 \(x+h_u-h_v\)。
推导不想写,每次增广后使 \(h_{i}\) 都加上 \(dis_i\) 即可实现过程一直非负。
code :
#include<bits/stdc++.h>
using namespace std;
const int M=150010,inf=2e9,N=4010;
int n,h[N],dis[N],first[N],s,t,head[N],ans,cnt,m;
bool vis[N];
struct edge
{int next,to,val,cost;
}e[M];
struct node
{int x,dis;bool operator<(const node &x)const{return x.dis<dis;}
};
void add(int x,int y,int u,int v)
{e[++cnt].to=y;e[cnt].next=first[x];e[cnt].val=u;e[cnt].cost=v;first[x]=cnt;e[++cnt].to=x;e[cnt].next=first[y];e[cnt].val=0;e[cnt].cost=-v;first[y]=cnt;
}
bool dijkstra(int s,int t)
{for(int i=1;i<=n;i++)dis[i]=inf,head[i]=first[i];priority_queue<node> q;q.push({s,0});dis[s]=0;while(!q.empty()){int u=q.top().x,d=q.top().dis;q.pop();if(d>dis[u])continue;for(int i=first[u];i;i=e[i].next){int to=e[i].to;if(e[i].val&&d+e[i].cost+h[u]-h[to]<dis[to]){dis[to]=d+e[i].cost+h[u]-h[to];q.push({to,dis[to]});}}}return (dis[t]<inf);
}
int dfs(int u,int flow)
{int temp=flow;if(u==t||!flow)return flow;vis[u]=1;for(int i=head[u];i;i=e[i].next){head[u]=i;int v=e[i].to,res=0;if(!vis[v]&&dis[v]==dis[u]+e[i].cost+h[u]-h[v]&&e[i].val&&(res=dfs(v,min(flow,e[i].val)))>0){ans+=res*e[i].cost;e[i].val-=res;e[i^1].val+=res;flow-=res;if(flow==0)return temp;}}vis[u]=0;return temp-flow;
}
int main()
{cnt=1;cin>>n>>m;t=n;for(int i=1;i<=m;i++){int a,b,c,d;cin>>a>>b>>c>>d;add(a,b,c,d);}int f=0;while(dijkstra(1,n)){memset(vis,0,sizeof(vis));f+=dfs(1,inf);for(int i=1;i<=n;i++)h[i]+=dis[i];}cout<<f<<" "<<ans;return 0;
}
无源汇上下界可行流
首先每条边流满下界 \(l\),然后建立一个新的图,各边流量为上界 \(r\) 与下界 \(l\) 之差 \(r-l\)。但是可能出现流量不平衡的情况。设立超级源点 \(S\),超级汇点 \(T\)。对于一个点:
- 该点入流比出流大,向 \(T\) 连一条容量为入流减出流的边。
- 该点出流比入流大,从 \(S\) 向该点连一条容量为出流减入流的边。
- 该点入流等于出流,不做操作。
然后跑最大流,如果源点流量流满则有可行流。
有源汇上下界可行流
在之前的基础上,将题目给出的源汇点连 \((t,s,inf)\) 的边,使之满足流量平衡。
有源汇上下界最大流
可行流中新连的 \((t,s,inf)\) 此时的流量即为一个可行流。然而可行流未必最大,需要在第一次的 \(Dinic(S,T)\) 后再来一次 \(Dinic(s,t)\)。
code :
#include<bits/stdc++.h>
using namespace std;
const int N=3010;
int cnt=1,n,m,s,t,tot,S,T,ans,inf=2147483647;
int num[N],fir[N],dis[N],vis[N],cur[N];
struct edge
{int to,w,nextt;
}e[200010];
void add(int u,int v,int w)
{e[++cnt].to=v,e[cnt].w=w,e[cnt].nextt=fir[u],fir[u]=cnt;e[++cnt].to=u,e[cnt].w=0,e[cnt].nextt=fir[v],fir[v]=cnt;
}
bool bfs()
{for(int i=0;i<=n+1;i++)dis[i]=0,vis[i]=false,cur[i]=fir[i];vis[S]=true,dis[S]=1;queue<int>q;q.push(S);while(!q.empty()){int u=q.front();q.pop();for(int i=fir[u];i;i=e[i].nextt){int v=e[i].to;if(vis[v]||e[i].w<=0)continue;dis[v]=dis[u]+1,vis[v]=1;if(v==T)return 1;q.push(v);}}return 0;
}
int dfs(int u,int flow)
{if(!flow||u==T)return flow;int used=0;for(int i=cur[u];i;i=e[i].nextt){int v=e[i].to;cur[u]=i;if(dis[u]+1!=dis[v])continue;int t=dfs(v,min(flow-used,e[i].w));if(!t)continue;e[i].w-=t,e[i^1].w+=t;used+=t;if(used==flow)return flow;}return used;
}
int dinic()
{int sum=0;while(bfs())sum+=dfs(S,inf);return sum;
}
int main()
{cin>>n>>m>>s>>t;S=0,T=n+1;for(int i=1;i<=m;i++){int u,v,low,upp;cin>>u>>v>>low>>upp;add(u,v,upp-low);num[v]+=low,num[u]-=low;}for(int i=1;i<=n;i++){if(num[i]>0){add(S,i,num[i]);tot+=num[i];}if(num[i]<0) add(i,T,-num[i]);}add(t,s,inf);ans=dinic();if(ans<tot){printf("please go home to sleep");return 0;}ans=e[cnt].w;S=s,T=t;e[cnt].w=e[cnt-1].w=0;ans+=dinic();cout<<ans;return 0;
}
答案即为 \(Dinic(s,t)\) 加上可行流。
可行流中新连的 \((t,s,inf)\) 此时的流量即为一个可行流。然而可行流未必最小,需要在第一次的 \(Dinic(S,T)\) 后再来一次 \(Dinic(t,s)\)。
答案即为可行流减去 \(Dinic(s,t)\) 。
有源汇上下界费用流
最大流换成费用流。
网络流 tricks & 典题
最大流の基本建模
对于此类建模问题,要考虑清楚一个流代表什么,其最大流代表什么,每一条边的容量代表什么,细细思考之后再开始码。
- P2754 [CTSC1999] 家园 / 星际转移问题
唯一难点只有周期性停靠太空站,不然就是傻逼题了。按时间分层,跑最大流。
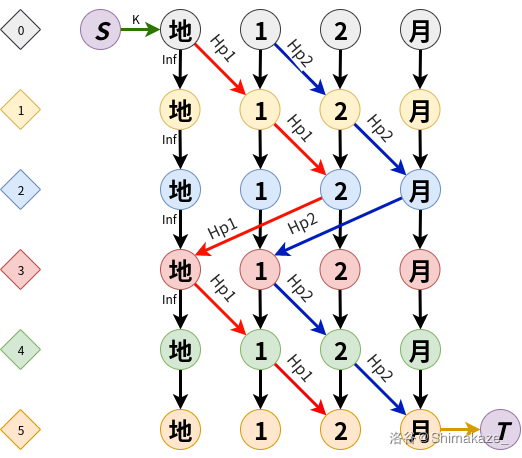
这个图就很好。这题中的流代表人,相同一个地点要向不同时间下的自己连边,注意只能从早的连到晚的,不然就时空穿梭了草。
- P2472 [SCOI2007] 蜥蜴
从一个柱子连到所有能跳到的柱子,容量为石柱耐久。因为每一只蜥蜴都不会跳回头路,所以每一点耐久都可以对应一个蜥蜴。源点连向所有有蜥蜴的柱子,所有能直接逃出界外的柱子连向汇点。
答案为最大流。
- P3254 圆桌问题
\(n+m\) 个点,代表 \(m\) 个单位与 \(n\) 个桌子。因为每个单位只有一个人能去到一个桌子,所以每个单位向每个桌子连容量为 \(1\) 的边。源点向每个桌子连容量为单位人数的边。如果最大流为人数之和则有可行方案,否则没有。本题中流代表人。
- P2764 最小路径覆盖问题
这是一类模型。
将图中每个点拆开,将一条路径视为合并两个路径。如果有一条边 \((x,y)\) 在原图中,那么连接 \((x,y+n)\),然后跑最大流。(其实就相当于一个二分图最大匹配)
模拟一下可以发现,这样跑最大流是满足条件的。而且只有没有合并的路径答案没有被计算上,所以答案为 \(n\) 减去最大流。
本题中的流意为将两个已经存在的路劲合并起来。
费用流の基本建模
- P2770 航空路线问题
拆点使只被访问一次,拆出来的两个点容量为 \(1\),费用为 \(1\)。将图中的边连上,注意只能从西边的城市走到东边的城市。第一个城市和最后一个城市拆出的边容量为 \(2\),费用为 \(1\) 的边。然后超级源点向最西边城市连容量为 \(2\),费用为 \(0\) 的边,最东边城市向汇点连容量为 \(2\),费用为 \(0\) 的边。跑最大费用最大流。最多城市即为费用。
此处的流代表选择这条边去走,费用代表走过这个城市。求和的东西一般要用费用来代表。
9.13
最大流の基本建模
- P2763 试题库问题
每个试题向每种属性连容量为 \(1\) 的边,每种属性向汇点连容量为该属性所需的边。方案输出就检查流量为 \(0\) 的边。
- P2766 最长不下降子序列问题
朴素 dp 解决第一问。如果 \(f_i \to f_j\) 是最优转移,则连边,这样每个流代表一个最长不降子序列,然后跑最大流。那些麻烦的限制就拆点然后限制流量。
- P4251 [SCOI2015] 小凸玩矩阵
二分 \(lim\),然后把该问题变成是否能找出至少 \(n-k+1\) 个数,使得这些数不大于当前 \(lim\) 且行列不同。最大流即可,源点向行连边,列向汇点连边,当前满足条件的数行列连边,然后判断最大流是否大于等于 \(n-k+1\)。
费用流の基本建模
- P1251 餐巾计划问题
首先,我们拆点,将一天拆成晚上和早上,每天晚上会受到脏餐巾(来源:当天早上用完的餐巾,在这道题中可理解为从原点获得),每天早上又有干净的餐巾(来源:购买、快洗店、慢洗店)。
从源点向每天晚上连一条费用为 \(0\),流量为当天所用餐巾的边,因为白天用完一定会剩下这么多脏餐巾。快洗就从 \(x\) 天晚上连到第 \(x+m\) 天早上,流量无限,费用为 \(f\),慢洗同理。放着不洗就连到下一天的晚上。从每天早上连向汇点,表示使用。流量流满则用完。从源点向每天早上连流量无限,费用为 \(p\) 的边。跑最小费用最大流。费用即为答案。
- P3356 火星探险问题
从一个格子连向能走到的格子,容量为无限。把有石头的格子拆成入点和出点,入点到出点容量为 \(1\),费用为 \(1\),对于能走到石头格子的格子,连向石头格子的入点,容量为 \(1\),连向石头格子的出点,容量为无限。最大费用最大流,流量为最多的能走的探测车,费用为石头数量。
- P3159 [CQOI2012] 交换棋子
将源点连向所有当前为 \(1\) 的点,将所有目标为 \(1\) 的点连向汇点,拆点,入点出点连边,容量皆为 \(1\)。对于每一个点,都拆开,费用为 \(1\),容量为 \(\frac{w_{i,j}}{2}\),如果这个点刚开始或者目标为黑色,那么容量为 \(1\),因为只可能被交换一次。每一个格子向八联通的点连容量无限,费用为 \(1\) 的边。流量意味着把黑点与自己交换过去,费用就是交换次数。跑最小费用最大流。最后答案即为费用
最小割の基本建模
此类问题,可以将思路视为“先全部选择,然后去掉一些东西使得满足某种条件”,即割。割的值最小即答案最大。
- P2762 太空飞行计划问题
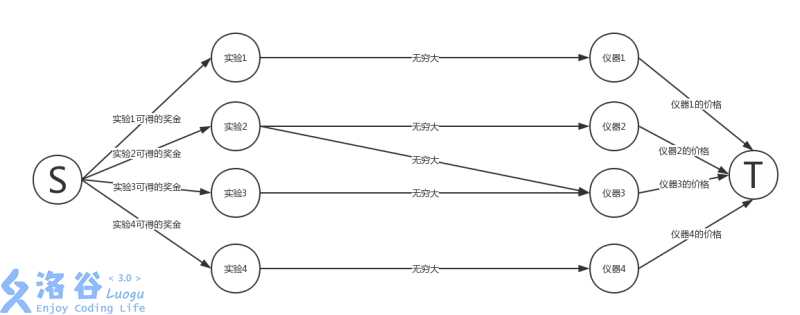
这样子连边。答案即为所有实验得到收益之和减去最小割。考虑割了一些器材的边相当于选择了那个实验,割了实验的边相当于不选择实验。
- P2774 方格取数问题
可以先取完所有点,然后考虑最小割割到满足条件为止。横纵坐标奇偶性相同的点放在二分图的一侧,对于相斥的那些点连边,容量无限。\(s\) 向这些点连边,边权为该点权。其他的点向 \(t\) 连边,边权为该点权。割掉一条边则相当于选择与他相斥的边(当然以后有可能因为别的东西被割掉)
答案即为所有点权减去最小割即可,P4474 王者之剑 同理。
UPD:很多黑白染色问题都是这样的,懒得写了。大概知道一下。