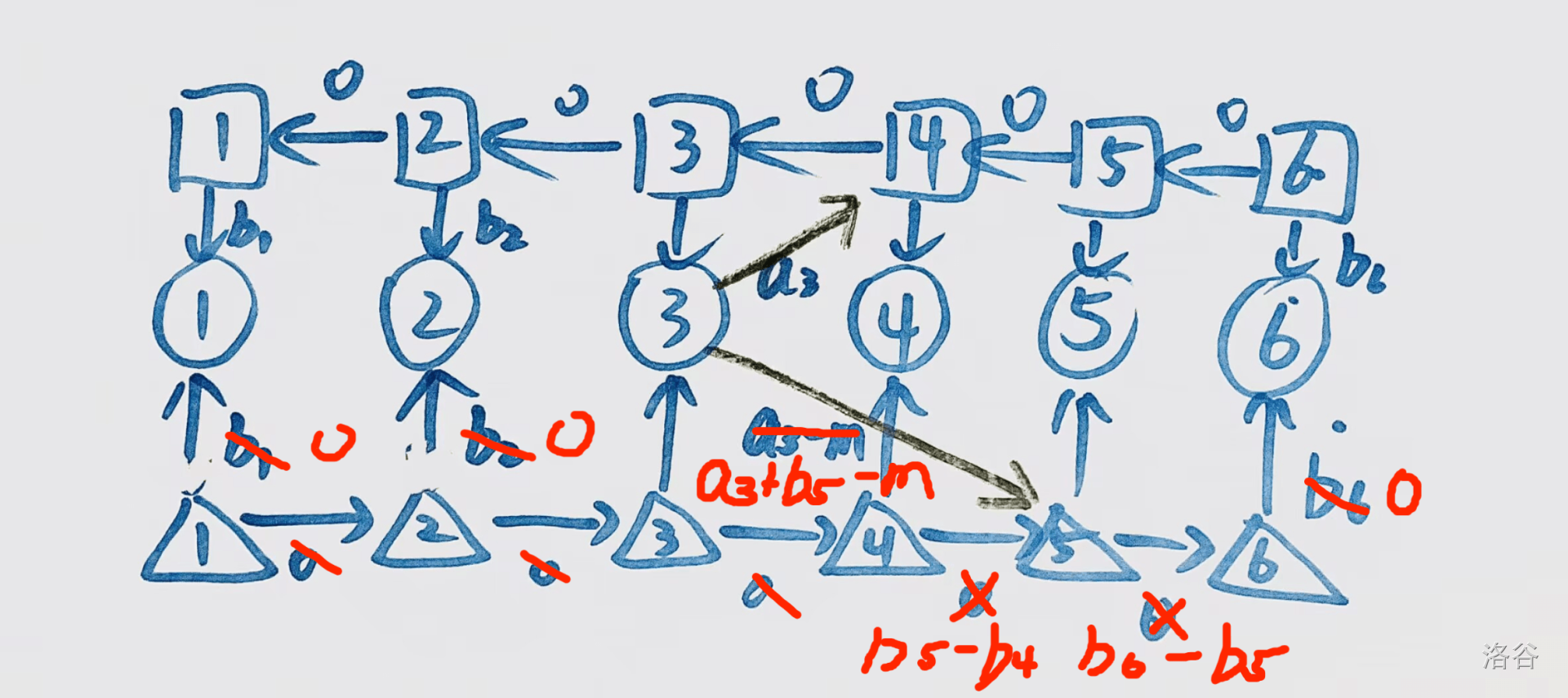
我们没有必要一定要将点值表示转化为系数表示,因为点值表示也可以进行单点求值,而且若点值连续,则还可以线性求值,与转化为系数表示之后没有区别。只需要求值的场合,完全可以只存连续的点值,然后线性的加法、减法、乘法、单点求值,甚至前缀和(线性)、函数复合(平方)。反而更优前途了。
我们现在有三种方法表示多项式了:系数表达(下分普通幂多项式和下降幂多项式)、点值表达。都可以用,而且各有所长。
拉格朗日插值可以解决点值表达的单点求值。下分非连续点值的单点求值(平方)和连续点值的单点求值(线性),见下。然后加、减、乘的操作,由 valarray 解决。转系数表达,详见本博客其它页面的多项式全家桶(或者少项式科技集)。
mint lagrange(const vector<pair<mint, mint>>& vec, mint x) {int n = (int)vec.size();mint ans = 0;for (int i = 0; i < n; i++) {mint num = 1, den = vec[i].second;for (int j = 0; j < n; j++) if (i != j) {den *= x - vec[j].first;num *= vec[i].first - vec[j].first;}ans += den / num;}return ans;
}
mint fac[200010], ifac[200010];;
mint lagrange(const vector<mint> &v, mint x) {int n = (int)v.size();fac[0] = 1;for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i;ifac[n] = 1 / fac[n];for (int i = n; i >= 1; i--) ifac[i - 1] = ifac[i] * i;mint ans = 0;vector<mint> tmp(n + 1);tmp[n] = 1;for (int i = n - 1; i >= 0; i--) tmp[i] = tmp[i + 1] * (i - x);mint pre = 1;for (int i = 0; i < n; i++) {mint num = ifac[i] * (i & 1 ? -1 : +1) * ifac[n - i - 1];mint den = v[i] * pre * tmp[i + 1];ans += den * num;pre *= i - x;}return ans;
}