

思路
这道题目首先要想,如何放置,才能让摄像头最小的呢?
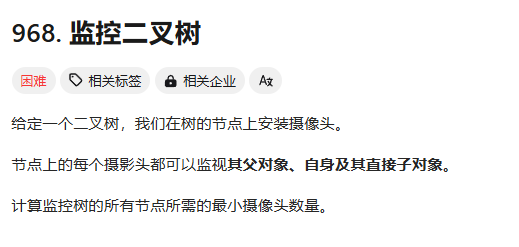
从题目中示例,其实可以得到启发,我们发现题目示例中的摄像头都没有放在叶子节点上!
这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。
所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。
那么有同学可能问了,为什么不从头结点开始看起呢,为啥要从叶子节点看呢?
因为头结点放不放摄像头也就省下一个摄像头, 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。
所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!
局部最优推出全局最优,找不出反例,那么就按照贪心来!
此时,大体思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
此时这道题目还有两个难点:
1. 二叉树的遍历
2. 如何隔两个节点放一个摄像头
确定遍历顺序
在二叉树中如何从低向上推导呢?
可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了。
如何隔两个节点放一个摄像头
此时需要状态转移的公式,先来看看每个节点可能有几种状态:
有如下三种(用数字表示):
- 该节点无覆盖——0
- 本节点有摄像头——1
- 本节点有覆盖——2
空节点属于哪种状态?为保证叶节点是无覆盖,让他的父节点放摄像头,空节点只能是有覆盖。如果空节点是无覆盖那叶节点就要放摄像头了。
由此确定递归的终止条件:
// 空节点,该节点有覆盖
if (cur == NULL) return 2;
再来看单层逻辑处理。主要有如下四类情况:
情况1:左右节点都有覆盖
情况2:左右节点至少有一个无覆盖的情况
情况3:左右节点至少有一个有摄像头
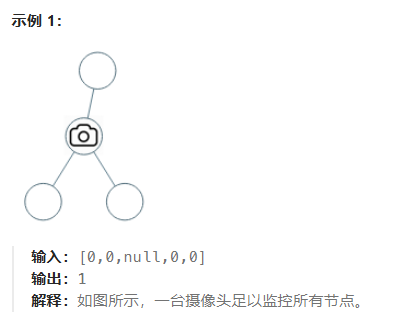
情况4:头结点没有覆盖
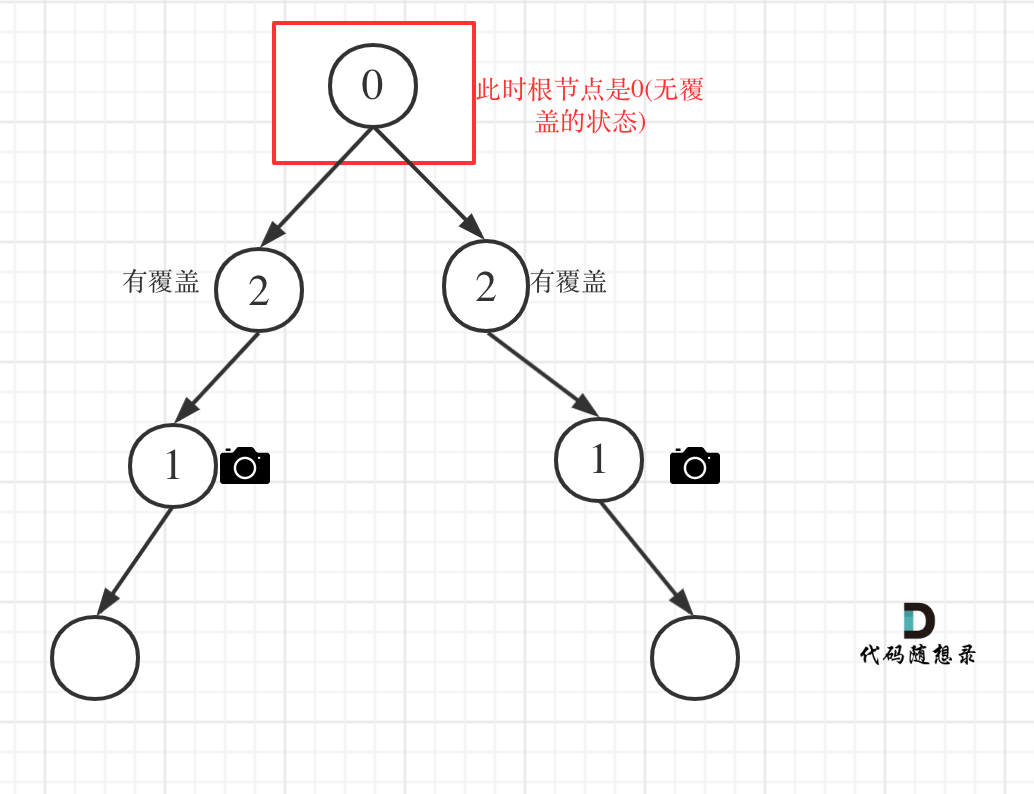
递归结束之后,还要判断根节点,如果没有覆盖,result++
代码如下:
int minCameraCover(TreeNode* root) {result = 0;if (traversal(root) == 0) { // root 无覆盖result++;}return result;
}
完整代码
class Solution {
public:int ans;int traversal(TreeNode* root){//空节点if(root == nullptr)return 2; //0-无覆盖,1-有摄像头,2-有覆盖//后序遍历int left = traversal(root->left);int right = traversal(root->right);//情况1:左右都有覆盖if(left == 2 && right == 2)return 0;//情况2:左右至少一个无覆盖if(left == 0 || right == 0){ans++;return 1;}//情况3:左右至少有一个有摄像头if(left == 1 || right == 1)return 2;return -1;}int minCameraCover(TreeNode* root) {if(traversal(root) == 0){ans++;}return ans;}
};