P3647 [APIO2014] 连珠线
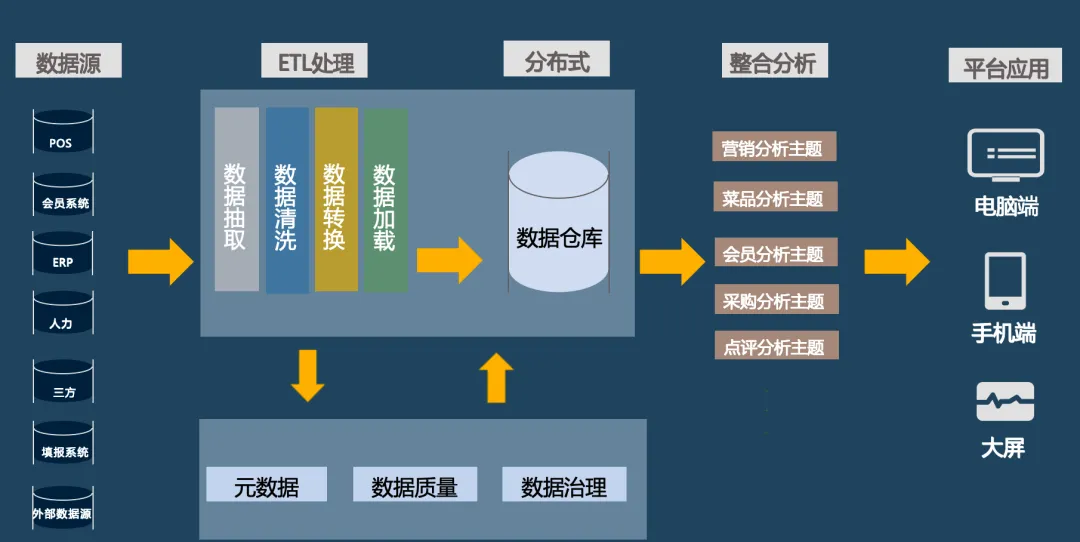
题意简述:树上加点游戏,分红蓝边,有边权,点编号为 \(1\) 到 \(n\)。游戏从任意一个点开始,每次操作添加一个新点 \(w\)。Append(w, v):连红边 \((w, v)\)。Insert(w, u, v):删掉红边 \((u, v)\),连蓝边 \((u, w)\) 和 \((w, v)\)。给定游戏结局的树,最大化最终蓝边总长度。
考虑简化操作。注意到存在最优解使所有 Append(u, v) 和 Insert(w, u, v) 相邻。合并这样的两操作,等价于指定旧点 \(u\),加新点 \(w\) 连蓝边 \((u, w)\),再加新点 \(v\) 连蓝边 \((w, v)\)。此时所有操作只涉及树边。设初始的那一个点为根。若给边定向,旧点指向新点,易得所有操作都在到根的链上,不拐弯。问题转化为在树上选出若干个长度为 \(3\) 的不拐弯的链,使边不重复,最大化边权和。\(f[u][0/1]\):点 \(u\) 父亲是/否被选。换根dp即可。