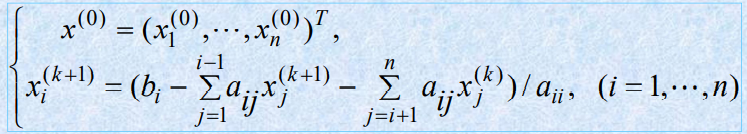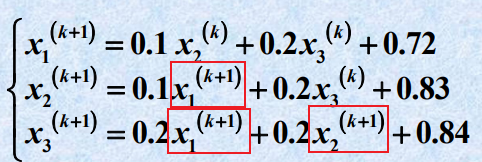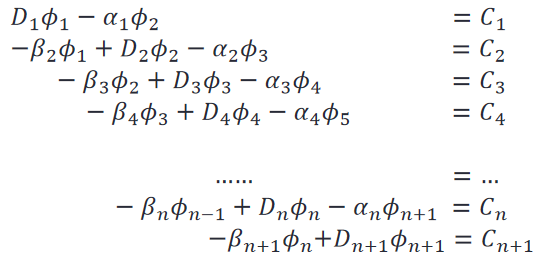6 求解三对角矩阵
背景
对于求解线性代数方程组\(Ax=B\),有两种方法:
-
直接法:通过有限步骤的算术运算求解线性方程组。
- 克拉默法则(Cramer's Rule)

这里D是矩阵A的行列式(det(A)),\(D_j\)是把矩阵A的第j列替换成b后求得的新矩阵A'的行列式。
- 矩阵求逆:\(x=A^{-1}B\)
- 高斯消元法:通过行变换,把A变成上三角矩阵,然后通过回代法求未知数。
- 上述方法的计算复杂度与方程组规模N的立方成正比,即\(\propto N^3\);此外,求解过程中,需要把系数矩阵A的所有\(N^2\)个元素都存储在计算机内存中。
-
非直接或迭代求解法:
-
雅可比迭代法:对k=0, 1, ..., 有
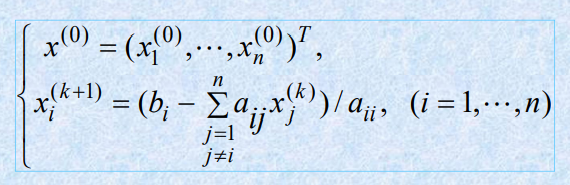
如:
\[\begin{equation}
\begin{aligned}
x_1^{(k+1)}&=\frac{b_1-\sum_{j=1,~j\ne i}^{n} a_{1j}\cdot x_j^{(k)}}{a_{11}}\\
&=\frac{1}{10}\cdot[7.2-(a_{12}\cdot x_2^{(k)}+a_{13}\cdot x_3^{(k)})]\\
&=0.1x_2^{(k)}+0.2x_3^{(k)}+0.72
\end{aligned}
\end{equation}
\]

上面的k就代表几次方,取\(x^{(0)}=(0,~0,~0)^T\),迭代求解即可。
-
高斯-赛德尔迭代法:是对雅可比迭代法的改进。
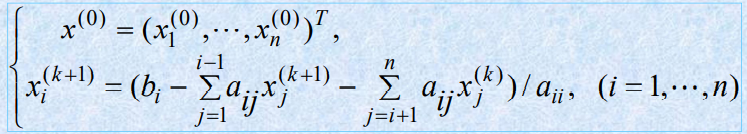
例:还是和上面的方程组一样,但是稍微变换一下,变成
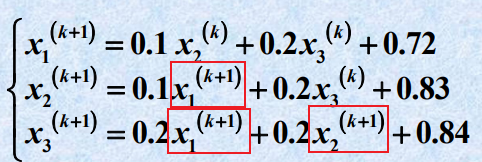
-
相比于直接法,迭代法的改进主要有:
- 每个迭代周期的总运算次数与 N 成正比。
- 方程中只有非零系数需要存储在核心内存中。
TDMA算法
基本
接下来,我们介绍三对角矩阵算法(Tri-Diagonal Matrix Algorithm, TDMA) ,这是一种针对一维情况的直接方法,通过逐行迭代的应用于多维问题的求解,计算成本低且所需存储空间最少。
设有如下三对角矩阵:
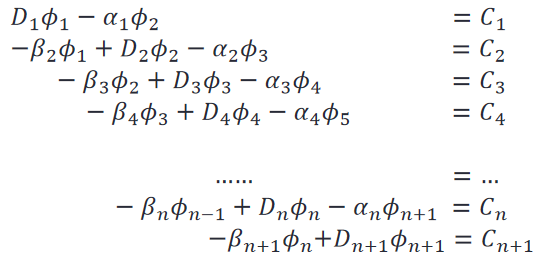
这里,我们首先认为\(\phi_1\)和\(\phi_{n+1}\)已由边界条件给出,作为已知量。
上述三对角矩阵的一般形式为:
\[\begin{equation}-\beta_j\phi_{j-1}+D_j\phi_j-\alpha_j\phi_{j+1}=C_j
\end{equation}
\]
转写一下,得:
\[\begin{equation}\begin{aligned}&\phi_{2}=\frac{\alpha_{2}}{D_{2}}\phi_{3}+\frac{\beta_{2}}{D_{2}}\phi_{1}+\frac{C_{2}}{D_{2}}\\&\phi_{3}=\frac{\alpha_{3}}{D_{3}}\phi_{4}+\frac{\beta_{3}}{D_{3}}\phi_{2}+\frac{C_{3}}{D_{3}}\\&\phi_{4}=\frac{\alpha_{4}}{D_{4}}\phi_{5}+\frac{\beta_{4}}{D_{4}}\phi_{3}+\frac{C_{3}}{D_{3}}\\&......\\&\phi_{n}=\frac{\alpha_{n}}{D_{n}}\phi_{n+1}+\frac{\beta_{n}}{D_{n}}\phi_{n-1}+\frac{C_{n}}{D_{n}}\end{aligned}
\end{equation}
\]
通过前向差分(forward elimination)和回代(back-sustitution),可以求解上述方程组。
前向差分
第一步,我们设法把式3的\(\phi_3\)方程中的\(\phi_2\)项替换掉,变成包含\(\phi_1\)的形式。
把第1个方程代入进去,得:
\[\begin{equation}\phi_3=\left(\frac{\alpha_3}{D_3-\beta_3\frac{\alpha_2}{D_2}}\right)\phi_4+\left(\frac{\beta_3\left(\frac{\beta_2}{D_2}\phi_1+\frac{C_2}{D_2}\right)+C_3}{D_3-\beta_3\frac{\alpha_2}{D_2}}\right)
\end{equation}
\]
引入两个参数\(A_2=\frac{\alpha_2}{D_2}\),\(C_2^{\prime}=\frac{\beta_2}{D_2}\phi_1+\frac{C_2}{D_2}\),得
\[\begin{equation}\phi_3=\left(\frac{\alpha_3}{D_3-\beta_3A_2}\right)\phi_4+\left(\frac{\beta_3C_2^{\prime}+C_3}{D_3-\beta_3A_2}\right)
\end{equation}
\]
进一步地,我们引入两个新的参数:\(A_3=\frac{\alpha_3}{D_3-\beta_3A_2}\quad\mathrm{and}\quad C_3^{\prime}=\frac{\beta_3C_2^{\prime}+C_3}{D_3-\beta_3A_2}\),修改后的结果为:
\[\begin{equation}\phi_{3}=A_{3}\phi_{4}+C_{3}^{\prime}
\end{equation}
\]
第二步,我们据此得到通用公式:
\[\begin{equation}\phi_j=A_j\phi_{j+1}+C_j^{\prime}
\end{equation}
\]
其中,两个系数:
\[\begin{equation}A_j=\frac{\alpha_j}{D_j-\beta_jA_{j-1}}\quad\mathrm{and}\quad C_j^{\prime}=\frac{\beta_jC_{j-1}^{\prime}+C_j}{D_j-\beta_jA_{j-1}}
\end{equation}
\]
应用边界条件:
- 对于点\(j=1\),令\(A_1=0\),\(C'_1=\phi_1\);
- 对于点\(j=n+1\),令\(A_{n+1}=0\),\(C'_{n+1}=\phi_{n+1}\)。
总结一下求解过程:
- 提取通项公式,如式2,此时\(\alpha_j\)(右边对角线的系数)、\(\beta_j\)(左边对角线的系数)、\(A_j\)(一个系数)和\(C_j\)(原方程右边的常数项)已知。
- 逐步计算其余方程的\(A_j\)和\(C'_j\),从\(j=2\)到\(j=n\)
- 由于\(\phi_{n+1}\)已知,倒序求\(\phi_n\),\(\phi_{n-1}\),...,\(\phi_2\)
TDMA的扩展:二维、三维
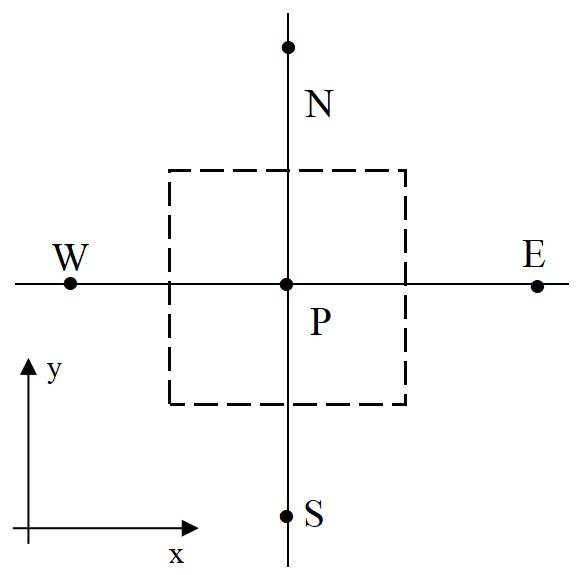
考虑一个二维的网格,就像SIMPLE算法里面所考虑的那样。
此时,离散化后的输运方程为:
\[\begin{equation}a_P\phi_P=a_E\phi_E+a_W\phi_W+a_N\phi_N+a_S\phi_S+b
\end{equation}
\]
为沿着南-北向使用TDMA,我们把上述方程重新排列成:
\[\begin{equation}a_W\phi_W-a_P\phi_P-a_E\phi_E=a_N\phi_N+a_S\phi_S+b
\end{equation}
\]
现在,我们假设上式的右边是“暂时地”(temporarily)已知,据此写出如下参数:
\[\begin{equation}\begin{array}{ccc}\alpha_j\equiv a_E,\beta_j\equiv a_W,D_j\equiv a_P&and&C_j\equiv a_N\phi_N+a_S\phi_S+b\end{array}
\end{equation}
\]
现在,沿着所选线的东-西向,解值\(j=2,~3,~4,~...~n\)。
下一步,把计算移动到另一条东-西向线。
在沿着北-南方向应用 TDMA 时,是从南向北逐条线推进的,因此当前节点的南侧节点\(\phi_s\)的值在前一条线的计算中已经被求得,可以认为是已知的;
而当前节点的北侧节点\(\phi_n\)的值是未知的,但每次迭代中,会使用上一次迭代结束时的值,或在第一次迭代时使用一个初始猜测值。
整个线迭代法需要重复多次,直到解收敛,即每次迭代之间的解的变化小于某个预设的容差值。
其核心思想是:
将一个二维离散化的运输方程通过线迭代法转化为一系列沿北-南方向的一维问题,然后利用 TDMA 高效求解这些一维问题。
在每次迭代中,通过假设相邻方向(这里是北和南)的节点值已知,将问题简化为三对角形式。
案例
题
对于一个圆柱形散热片(cylindrical fin),考虑一维稳态导热/对流换热。
左侧边界的温度是100\(^{\circ}C\),右侧边界是绝热的,因此通过右侧边界的热通量为零。
该圆柱形散热片被放在20\(^{\circ}C\)温度的环境中。
在这种情况下的一维热传导方程为:
\[\begin{equation}\frac{d}{dx}\left(kA\frac{dT}{dx}\right)-hP(T-T_\infty)=0
\end{equation}
\]
其中,h是对流换热系数,P是周长(perimeter),k是材料导热系数,\(T_{\infin}\)是环境温度。
要求:计算沿着散热片的温度分布。
已知:散热片长度\(L=1~m\),\(\frac{hP}{kA}=25~m^{-2}\)。
解
由于该问题被简化为一维稳态导热/对流换热,构建网格设置如下:
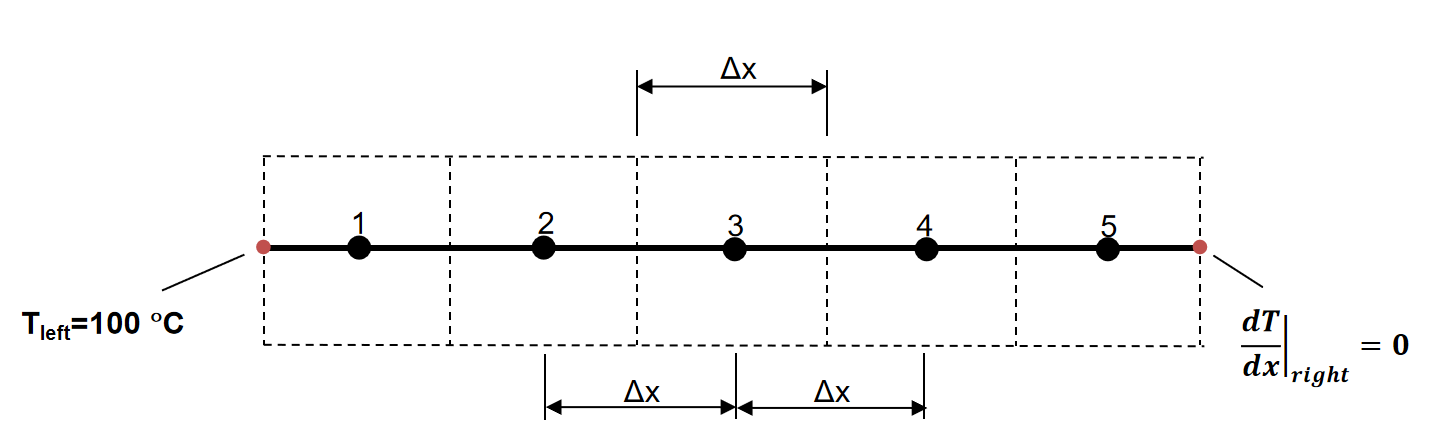
对于中间的节点2、3、4,把方程离散化如下:
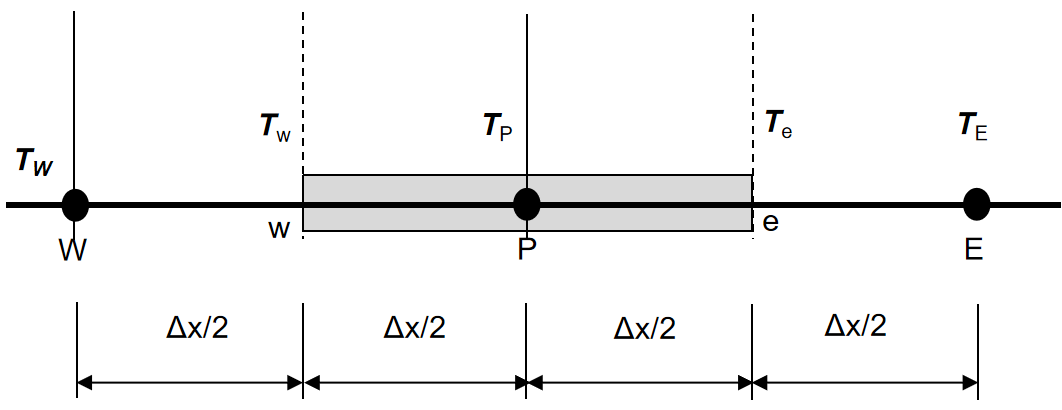
第一步相当于给方程12的两边乘以\(\Delta x\):
\[\begin{equation}\left(\mathrm{k}A\frac{dT}{dx}\right)_e-\left(\mathrm{k}A\frac{dT}{dx}\right)_w-\Delta\mathrm{x}hP(T_P-T_\infty)=0
\end{equation}
\]
第二步是先把两边同时除以kA,然后把东侧和西侧节点的温度变化dT离散化:
\[\begin{equation}\left(\frac{T_E-T_P}{\Delta\mathrm{x}}\right)-\left(\frac{T_P-T_W}{\Delta\mathrm{x}}\right)-\Delta\mathrm{x}\frac{hP}{\mathrm{k}A}(T_P-T_\infty)=0
\end{equation}
\]
第三步,在等式两边同时乘以\(\Delta x\),然后把各个温度独立出来:
\[\begin{equation}T_W-\left(\Delta\mathrm{x}\Delta\mathrm{x}\frac{hP}{\mathrm{k}A}+2\right)T_P+T_E=-\Delta\mathrm{x}\Delta\mathrm{x}\frac{hP}{\mathrm{k}A}T_\infty
\end{equation}
\]
第四步,已知\(\frac{hP}{kA}=25\),又根据散热片总长L=1 m,可知单个网格长度\(\Delta x=\frac{1}{5}~m\),计算可得\(\Delta\mathrm{x}\Delta\mathrm{x}\frac{hP}{\mathrm{k}A}=1\),故有:
\[\begin{equation}T_W-3T_P+T_E=-20
\end{equation}
\]
对于左边的端节点1:
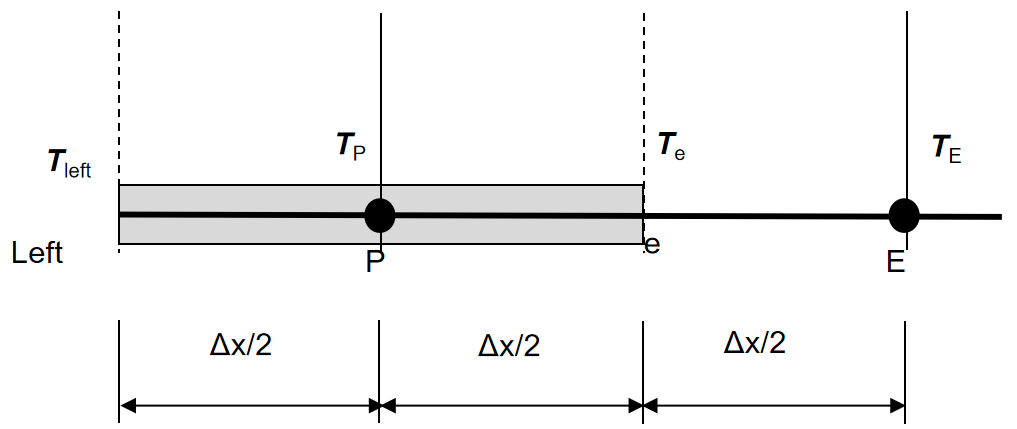
热传导方程乘以\(\Delta x\)为:
\[\begin{equation}\left(\mathrm{k}A\frac{dT}{dx}\right)_e-\left(\mathrm{k}A\frac{dT}{dx}\right)_{left}-\Delta\mathrm{x}hP(T_P-T_\infty)=0
\end{equation}
\]
下一步和中间节点的处理相比,有一点不同,把左侧边界的dx变成0.5\(\Delta x\):
\[\begin{equation}\left(\frac{T_E-T_P}{\Delta\mathrm{x}}\right)-\left(\frac{T_P-T_{left}}{0.5\Delta\mathrm{x}}\right)-\Delta\mathrm{x}\frac{hP}{\mathrm{k}A}(T_P-T_\infty)=0
\end{equation}
\]
然后同样是提温度、算系数,得到:
\[\begin{equation}-4T_P+T_E=-220
\end{equation}
\]
最后是对右侧节点5的处理:
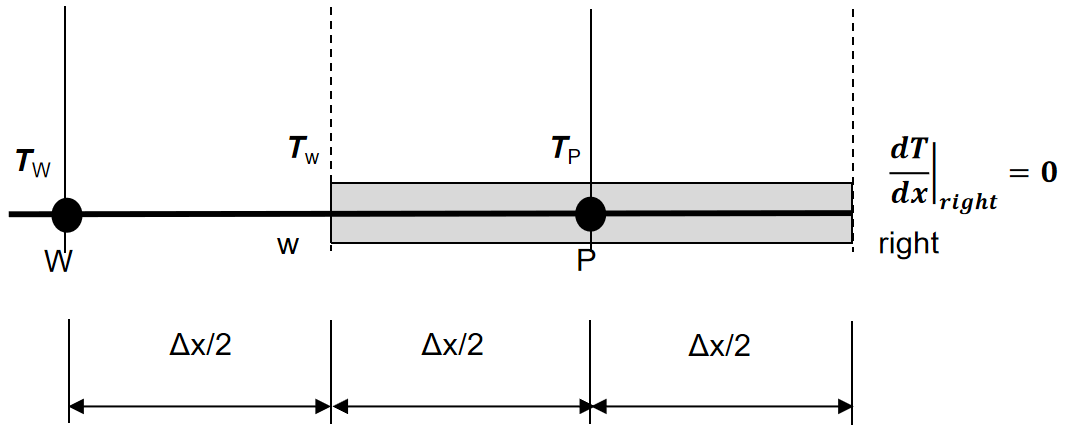
\[\begin{equation}\left(\mathrm{k}A\frac{dT}{dx}\right)_{right}-\left(\mathrm{k}A\frac{dT}{dx}\right)_{w}-\Delta\mathrm{x}hP(T_{P}-T_{\infty})=0
\end{equation}
\]
注意到边界条件\(\frac{dT}{dx}|_{right}=0\),就只剩西侧节点的直接热传导了:
\[\begin{equation}-\left(\frac{T_P-T_W}{\Delta\mathrm{x}}\right)-\Delta\mathrm{x}\frac{hP}{\mathrm{k}A}(T_P-T_\infty)=0
\end{equation}
\]
同样,乘以\(\Delta x\)、代入已知数,得:
\[\begin{equation}-2T_P+T_W=-20
\end{equation}
\]
结合公式16、19、22,再缩放一下系数大小,可得:
\[\begin{equation}\begin{bmatrix}20&-5&0&0&0\\-5&15&-5&0&0\\0&-5&15&-5&0\\0&0&-5&15&-5\\0&0&0&-5&10\end{bmatrix}\begin{bmatrix}T_1\\T_2\\T_3\\T_4\\T_5\end{bmatrix}=\begin{bmatrix}1100\\100\\100\\100\\100\end{bmatrix}
\end{equation}
\]
接下来就是求解这个三对角矩阵了。
回顾TDMA的通用形式:
\[\begin{equation}-\beta\phi_{j-1}+D_j\phi_j-\alpha_j\phi_{j+1}=C_j
\end{equation}
\]
对于节点1和5,可令\(\beta_1 = 0\),\(\alpha_5 = 0\)。而在边界处的物理量\(\phi\)(这里是温度T)没有使用,而是通过最右边的源项\(C_j\)进入计算。
回顾一下,通项公式:
\[\begin{equation}\phi_j=A_j\phi_{j+1}+C_j^{\prime}
\end{equation}
\]
两个系数:
\[\begin{equation}A_j=\frac{\alpha_j}{D_j-\beta_jA_{j-1}}\quad\mathrm{and}\quad C_j^{\prime}=\frac{\beta_jC_{j-1}^{\prime}+C_j}{D_j-\beta_jA_{j-1}}
\end{equation}
\]
计算结果如下:
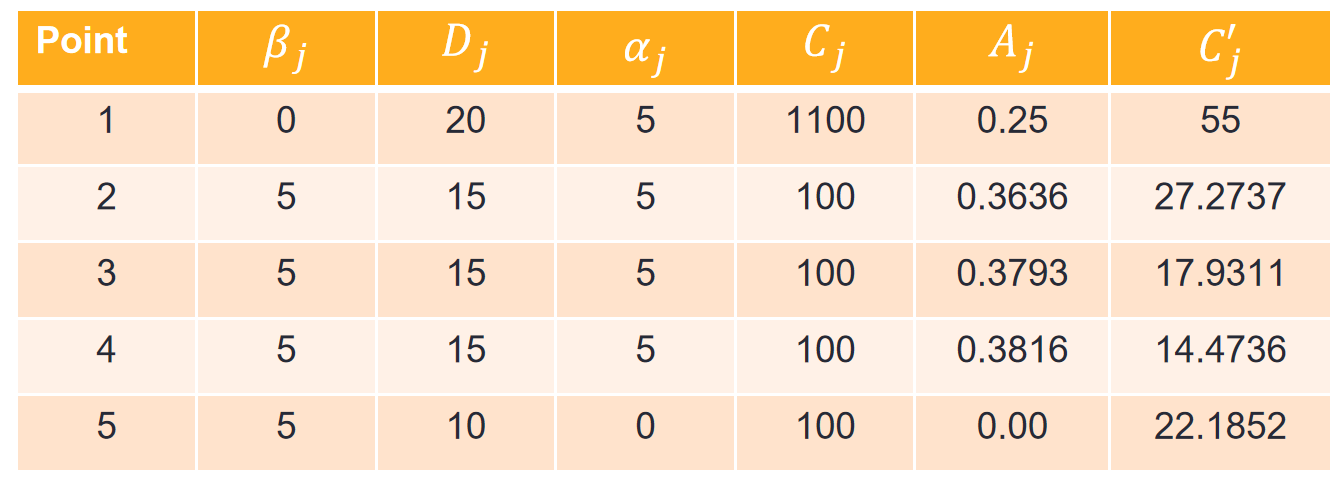
其具体计算过程如下:
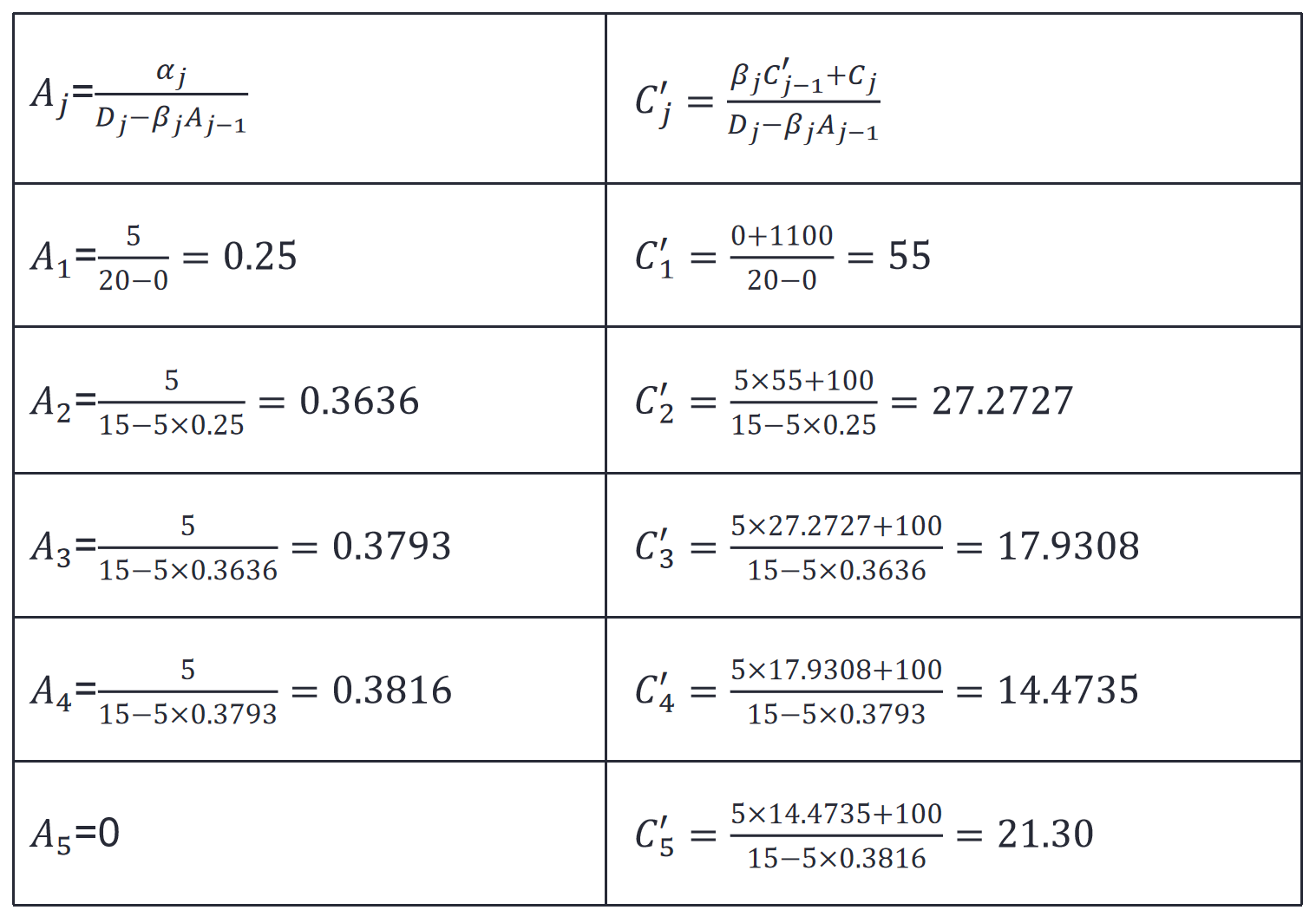
把上述结果回代到式25,具体数值计算步骤和结果如下:

至此,我们就完成了该圆柱散热片上,各节点的温度分布计算。

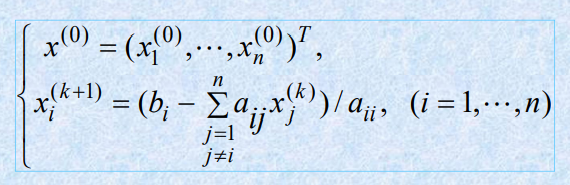
 \[\begin{equation} \begin{aligned} x_1^{(k+1)}&=\frac{b_1-\sum_{j=1,~j\ne i}^{n} a_{1j}\cdot x_j^{(k)}}{a_{11}}\\ &=\frac{1}{10}\cdot[7.2-(a_{12}\cdot x_2^{(k)}+a_{13}\cdot x_3^{(k)})]\\ &=0.1x_2^{(k)}+0.2x_3^{(k)}+0.72 \end{aligned} \end{equation} \]
\[\begin{equation} \begin{aligned} x_1^{(k+1)}&=\frac{b_1-\sum_{j=1,~j\ne i}^{n} a_{1j}\cdot x_j^{(k)}}{a_{11}}\\ &=\frac{1}{10}\cdot[7.2-(a_{12}\cdot x_2^{(k)}+a_{13}\cdot x_3^{(k)})]\\ &=0.1x_2^{(k)}+0.2x_3^{(k)}+0.72 \end{aligned} \end{equation} \]